Konsekwencje drugiego postulatu Einsteina

Część #1: Wprowadzenie
...

Część #6: Relatywistyczny przyrost masy, pędu i energii

Część #7: Konsekwencje drugiego postulatu Einsteina

- Panie doktorze, gdzie się dotknę, to mnie boli.
- Ma pani bolący palec.

Można powiedzieć, że podobnie jest z prędkością fotonu. Gdziekolwiek w próżni ją zmierzymy, zawsze uzyskamy wartość c. Bohaterka dialogu wywnioskowała, że boli ją całe ciało, a obserwator uznał, że foton porusza się z prędkością c względem wszystkiego jednocześnie. W obu przypadkach uzyskujemy obraz rzeczywistości wykreowany poprzez fakt pomiaru.

Fotony rozświetlają świat wokół nas i aż trudno uwierzyć, że w czasie podróży są całkowicie niewidoczne, rejestrujemy je dopiero, gdy dotrą do odbiornika. Dopiero wtedy na podstawie dokonanych pomiarów oraz przyjętych założeń, jesteśmy w stanie wnioskować o drodze kwantu światła.

Poniżej udowodnimy, jak mylące może to być wyobrażenie.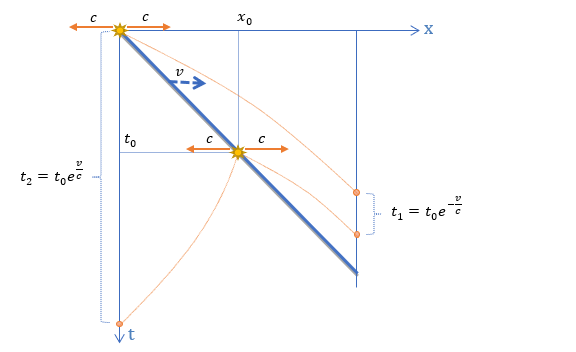

Niech v oznacza prędkość, z jaką cząstka porusza się wewnątrz pudełka. Na rysunku tor cząstki oznaczono ukośną, ciągłą linią. Cząstka emituje falę EM o częstotliwości f0=1/t0, gdzie t0 jest okresem tej fali. Przeanalizujmy dwa kolejne grzbiety tej fali. Pojedynczy grzbiet fali przypomina sferą propagującą we wszystkich kierunkach z prędkością c. Na jednowymiarowej osi x z rysunku moment emisji każdego grzbietu zaznaczono strzałkami skierowanymi w przeciwne strony.

W chwili t=0 wyemitowany został pierwszy grzbiet fali. Następnie w chwili t=t₀ został wyemitowany drugi grzbiet fali. Z dotychczasowych rozważań wiemy (wyprowadzenie wzoru tutaj), że grzbiety wyemitowane w odstępie czasu t₀ dotrą do jednej ścianki w odstępie czasu t₁=t₀ e^-v/c, a do drugiej ścianki w odstępie czasu t₂=t₀e^v/c.

Pamiętamy, że foton w czasie podróży jest niewidoczny, wyemitowany sygnał rejestrujemy dopiero na ściankach pudełka. Czy obserwator jest w stanie ustalić prędkość cząstki jedynie na podstawie zmierzonych czasów t₁ i t₂?

My patrząc na rysunek wiemy, że cząstka porusza się z prędkością v i rozumiemy całe zjawisko, bo je widzimy. Ale rzeczywisty obserwator tego nie wie. Co ma biedny zrobić, aby poznać prędkość cząstki? Musi przyjąć jakieś dodatkowe założenie, bo sama rejestracja czasów t₁ i t₂ jest niewystarczająca. I tutaj z nieocenionym wsparciem procesu dedukcji naszego obserwatora przychodzi drugi postulat Einsteina o stałej prędkości c fotonu względem brzegów pudełka. Zobaczmy, jak ten postulat wpływa na wyobrażenie ruchu cząstki. Wyliczymy wg tego założenia prędkość V poruszającego się źródła promieniowania.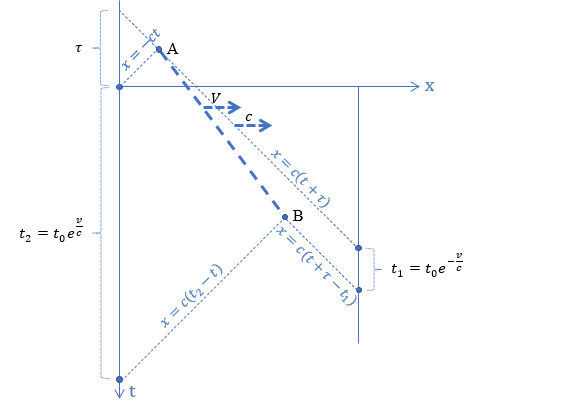

Postulat o stałej prędkości światła oraz dokonane pomiary czasów t₁ i t₂ pozwalają z prostych zależności geometrycznych wyznaczyć miejsce na wykresie, z którego musiał być wyemitowany każdy grzbiet fali. Współrzędne emisji pierwszego grzbietu oznaczmy A (x_A,t_A), natomiast współrzędne emisji drugiego grzbietu oznaczmy B (x_B,t_B). Parametr τ na rysunku uwzględnia dowolność chwili emisji sygnału.

Punkt A (x_A,t_A) możemy wyznaczyć z przecięcia prostych x=-ct i x=c(t+τ),

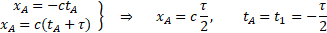
a punkt B (x_B,t_B) z przecięcia prostych x=c(t₂-t) i x=c(t+τ-t₁).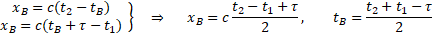

A zatem mamy już wszystko co potrzeba, żeby obliczyć prędkość V, z jaką przemieszcza się źródło promieniowania zgodnie z drugim postulatem Einsteina.

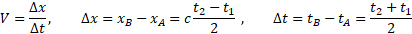
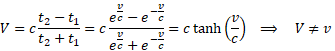
Przyjrzyjmy się uzyskanej zależności. Otrzymany wynik jest wręcz szokujący! Drugi postulat Einsteina spowodował, że otrzymaliśmy wynik sprzeczny z założeniem, od którego wyszliśmy.

No cóż… Jesteśmy zmuszeni uznać to za bezpośredni dowód, że nasze wyobrażenie ruchu, oparte na postulacie stałej prędkości światła c względem ścianek pudełka, nie odpowiada rzeczywistości.

A teraz przypomnijmy sobie, jakim wzorem określona jest prędkość w Teorii Względności (prędkość Lorentza v_L).

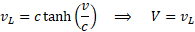
Cóż za niespodzianka! Okazuje się, że nasze wyobrażenie prędkości cząstki V jest równe prędkości Lorentza v_L. Rzeczywiście występująca w Teorii Względności wielkość v_L z definicji funkcji tanh nie może przekroczyć prędkości światła, nawet jeśli prędkość cząstki v będzie dowolnie większa od c. Przykładowo mion, któremu przypisano prędkość v_L=0,99c w rzeczywistości porusza się z prędkością v = atanh(0,99)c ≅ 2,65c i zdąży dolecieć do Ziemi zanim się rozpadnie (zakładając czas życia mionu 2,2μs oraz to, że powstał 20km nad ziemią).

Niniejsze odkrycie zmusza nas do ważnej konstatacji:

Prędkość Lorentza v_L dotyczy tylko naszego wyobrażenia ruchu cząstki, która w rzeczywistości porusza się z prędkością v.

Zestawmy oba tory ruchu na jednym rysunku.

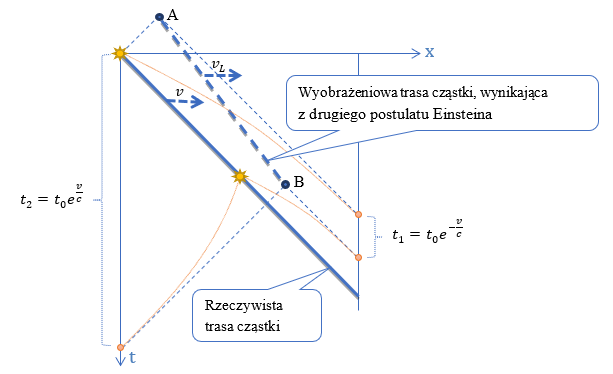
Na podstawie obiektywnych matematycznych wyliczeń pokazaliśmy różnicę między prędkością v i v_L. W efekcie realna prędkość jest w naturalny sposób addytywna v₃=v₁+v₂, a tę wyobrażeniową musimy dodawać za pomocą matematyki .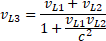

Widzimy, jak mylące może być wyobrażenie ruchu w sytuacji, gdy wiedzę o zjawisku czerpiemy z założenia o absolutnie stałej prędkości światła względem obserwatora.

Zależności wynikające z Teorii Względności były wielokrotnie weryfikowane i są w pełni zgodne z obserwacjami. Każda nowa teoria musi przede wszystkim uznać fakty doświadczalne, a jednocześnie wnosić jakąś wartość dodaną. W przypadku Modelu Naturalnego wartością dodaną jest dokładny opis zjawiska na bazie klasycznych wyprowadzeń bez paradoksów i magicznego skracania odległości. A zgodność ze wzorami relatywistycznymi jest tu automatycznie zapewniona przez spójny obraz wynikowych zależności. Używając funkcji v_L(v) mamy wzory STW, a odwołując się do prędkości v (przez podstawienie v_L(v)=c tanh(v/c)) otrzymujemy równoważne formuły w Modelu Naturalnym. Potwierdzeniem tej zgodności są wyprowadzone wcześniej wzory na masę, pęd i energię. Innym przykładem może być ruch cząstki pod wpływem stałej siły. Poniżej pokażemy w jaki sposób wzory znane z relatywistycznych wyprowadzeń, uzyskujemy w oparciu o zwykłą, addytywna prędkość v.

Ruch cząstki pod wpływem stałej siły

Pamiętamy wyrażenie opisujące pęd z wykorzystaniem prędkości cząstki v. Na podstawie tego pędu obliczmy siłę F, z jaką wypromieniowana fala EM działa ma pudełko:

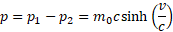
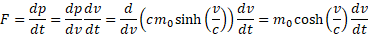
Uzyskany wynik pozwala znaleźć przyśpieszenie α cząstki wywołane przez siłę F:

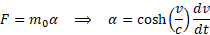
Zauważmy, że stała siła F oznacza stałe przyspieszenie α, pozwala to pozbyć się pochodnej z powyższego wzoru.

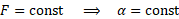
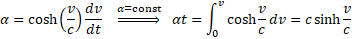
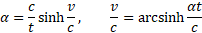
Korzystając z przyśpieszenia α możemy wyrugować z dalszych obliczeń prędkość v, co powoduje, że uzyskane wyniki są tożsame ze wzorami Teorii Względności.

Podstawiając ostatnią zależność do wyprowadzonej wcześniej formuły na energię, uzyskujemy dokładnie ten sam wzór, który dobrze znamy z relatywistycznych wyliczeń:

Także przyrost energii ΔE spowodowany działaniem siły F, czyli energię kinetyczną cząstki, zapiszemy znanym wzorem:

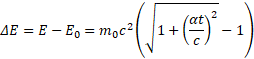
A jaką drogę x pokonuje cząstka pod wpływem przyśpieszenia α?

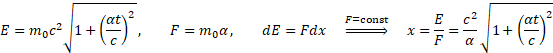
To kolejny wynik dobrze znany z mechaniki relatywistycznej. Jednak taki sam wynik nie oznacza tego samego obrazu rzeczywistości, który opisuje.

Podsumowując, Model Naturalny respektuje (a wręcz potwierdza) przedstawione wzory Szczególnej Teorii Względności, a jednocześnie daje im logiczne wytłumaczenie bez paradoksów, zgodne klasycznym doświadczeniem ruchu. Zaprezentowana w opracowaniu zrozumiała istota zjawiska pozwala przewidywać i wyciągać nowe wnioski. A fakt istnienia prędkości dowolnie większych od prędkości światła zmienia nasze postrzeganie zarówno procesów kosmologicznych, jak też może być wytłumaczeniem zjawisk rejestrowanych lokalnie.

W następnej notce ciekawa właściwość przestrzeni, która na podstawie lokalnych pomiarów pozwala wnosić o odległym położeniu obiektów w tej samej chwili jednoczesności.