Część pierwsza znajduje się tutaj:
pannamigotka.salon24.pl/175971,geometria-blizej-fizyki-kwantowej
A oto część druga:
Fizyczne właściwości okręgu a jego geometria obserwowana w wymiarze krzywizny.
Stany fazowe – liniowe
Doświadczenie 1.
Weźmy gumkę aptekarską. Ma ona obwód L = 2 pi 1 i przyjmujemy, że znajduje się ona w stanie o krzywiźnie dodatniej, gdyż jej promień R = 1. Skręcamy teraz gumkę tak, żeby jej obwód utworzył dwa małe okręgi połączone ze sobą czyli w rezultacie tworzy się jeden podwójny mały okrąg. A teraz skręćmy tak, by utworzył potrójny... itd. (Teoretycznie taką gumkę można by skręcać aż do punktu – malutkiej kulki). Można powiedzieć, że dostarczamy gumce energii, a ona zmienia swoją geometrię – skraca się jej promień i zwiększa się geometryczna krzywizna gumki. Jeśli przestaniemy dostarczać jej energii, to gumka zacznie rozwijać się sama do postaci o „najniższej energii” i krzywiźnie k = 1, do swojego „stanu podstawowego” – można by powiedzieć.
Skręcając gumkę zauważymy, że w stanie podstawowym o najniższej energii (nieskręcona gumka leżąca na stole) jest styczna z blatem stołu czyli z naszą euklidesową płaszczyzną odniesienia o zerowej krzywiznie, ale im bardziej jest ona skręcona, tym mniej przylega do blatu stołu – płaszczyzny euklidesowej. Stan, gdy gumka przylega całkowicie do blatu stołu możemy nazwać jej stanem podstawowym, a stany pełnych skrętów stanami fazowymi skręcanej gumki. Stany przejściowe występujące pomiędzy kolejnymi pełnymi skrętami (fazowymi) możemy nazwać międzyfazowymi stanami turbulencyjnymi.
Podobnie, gdybyśmy nagrali film z gumką rozkręcającą się z postaci o pewnej maksymalnej gęstości skrętu do postaci rozkręconego całkowicie okręgu i puścili go w zwolnionym tempie, zobaczylibyśmy, że obwód gumki jest zawsze stały, tylko że jest „łamany” czyli skręcany lub rozkręcany w wyższej wymiarowości – w trójwymiarowej przestrzeni euklidesowej. Promień zaś, przy kolejnych skrętach gumki (okręgu) zmienia się: "łamie się" na jego składowe – pod-promienie (wektory), które przyjmują wartości ułamkowe.
W stanie fazowym wartości składowe „pod-promieni” (wektorów) związane są z ilością pod-okręgów. W stanach fazowych wartości ułamkowe promieni pod-okręgów (wektorów) są sobie równe, a ich suma zawsze jest równa promieniowi R = 1. A w międzyfazowych stanach turbulencyjnych wartości pod-promieni (wektorów) są zróżnicowane, jednak ich suma także zawsze jest równa wartości promienia R = 1.
Dwa małe okręgi są równoważne z jednym dużym, ale duży i dwa małe różnicuje inna wymiarowość krzywizny przestrzennej. Okrąg uległ skokowi kwantowemu ( z jednego stanu „fazowego” do następnego) z 2 π 1 do 4 π ½ = 2 x 2 π R/2. Teraz połowa gumki pozostaje na jednej dwuwymiarowej płaszczyźnie, a druga połowa znajduje się poza tą płaszczyzną euklidesową (w „zaświecie wymiarowym”).
W trakcie eksperymentu gumka zmienia swoją geometrię w dodatkowych wymiarach (przestrzeni 3D), ale dla uproszczenia możemy uznać, że zmiany te zachodzą w wymiarze krzywizny. Wówczas obserwujemy, że przechodzenie od pierwszego stanu gumki o geometrii 2 π r do stanu o geometrii 2 x 2 π R/2 (podwójnego skrętu) odbywa się w przestrzeni poza jedną płaszczyzną euklidesową. Zmiana ta powoduje zmianę krzywizny przestrzeni zajmowanej przez gumkę. Natomiast na dwuwymiarowej płaszczyźnie mogą być zaobserwowane na przykład pewne stany, w których zachodzi “skręcanie” gumki do podwójnego, potrójnego, poczwórnego itd. okręgu. Ale na dwuwymiarowej płaszczyźnie euklidesowej zawsze możemy przedstawić tylko i wyłącznie „jedną warstwę” powielonych pod-okręgów o geometrii 2 pi r (gdzie r przyjmuje wartości ułamkowe). Rys. 8
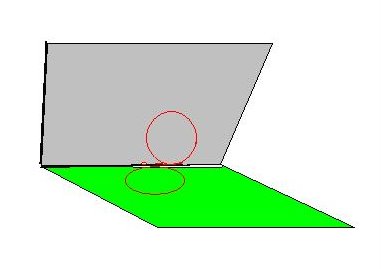
Gdybyśmy dwie płaszczyzny skleili ze sobą, wówczas obserwator mógłby zaobserwować taki stan jako jeden okrąg o ciut grubszym obwodzie. Wtedy będzie to miało konsekwencje dla fizycznych właściwości okręgu, ale o tym później. Obserwator może dokonywać obserwacji jedynie na jednej z tych płaszczyzn (zielona lub szara). Zmiana krzywizny z 2 π na 4 π nastąpiła z jednoczesną zmianą długości promienia z R = 1 na r = ½. Zmianę tę wymusiło “zapętlenie” (skręt) pojedyńczego okręgu do podwójnego okręgu o promieniu o połowę mniejszym.
Oto mamy możliwość obserwowania okręgów o różnym promieniu jako różnych stanów meta-okręgu zmieniającego swoją geometrię zgodnie ze wzorem L = k * 2 π R/n. Przyjmujemy, że R = 1. Jak zakrzywia się okrąg? Kiedy obserwujemy skrócenie promienia okręgu jako danego stanu okręgu, przyjmujemy, że spowodowane jest ono kolejnymi „zawinięciami” tego okręgu. Mamy takie oto przekształcenie:
L = 2 π R = n * 2 π r
inaczej:
L = k * 2 π R/n
W tym wzorze: L = k * 2 π R/n
„k” oraz „n” jako liczby są sobie równe, jednak nie są równoważne jakościowo, ponieważ:
n – wyznacza ilość pod-okręgów
k – wyznacza wartość krzywizny
Dla każdego z obu małych okręgów wartości L i R zmalały o połowę. Przy okazji zjawiska skręcania gumki występuje geometryczne zwiększenie krzywizny polegający na zwielokrotnianiu się pod-okręgów: 2 x 2 π rR2, 3 x 2 π R/3, 4 x 2 π R/4 itd… czyli L = k * 2 π R/n. W ten sposób wartości wymiaru krzywizny określają zmienne wielokrotności „k”. Przyjrzyjmy się stanowi, który możemy zapisać jako
3 x 2 π r/3. Teraz mamy trzy płaszczyzny: 2 π r +2 π r + 2 π r = L. rys.9
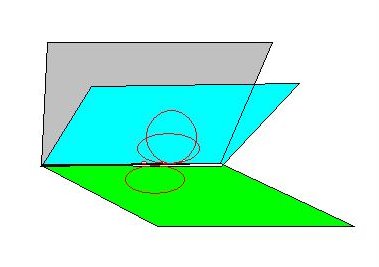
Ten stan możemy zapisać jako: L = 3 x 2 π 1/3. Jest to stan fazowy (liniowy), podobnie jak inne stany tego typu: 2 π 1, 2 x 2 π ½ , 4 x 2 π ¼, 5 x 2 π 1/5 , 6 x 2 π 1/6 , 7 x 2 π 1/7 itd.
Zmiana wielokrotności liczby „pi” wraz ze zmianą - „łamaniem” długości promienia R = 1 na pod-promienie (wektory) zachodzi w sposób ciągły, ale nie jest to w tym momencie obserwowalne na dwuwymiarowej płaszczyźnie euklidesowej. Dla obserwatora z płaszczyzny euklidesowej parametry zmian (dane) dotyczące jej kolejnych skrętów są „zmiennymi ukrytymi” w wyższej wymiarowości.
Sprawdźmy dwa przejścia (przeskoki) fazowe:
1) 2 π 1 --> 2 π ½ promień zostaje skrócony - fałsz
2) 2 π 1 --> 4 π ½ promień widzimy jako skrócony, ponieważ krzywizna w wyższej wymiarowości uległa zmianie na dodatnią – prawda
oraz
3) 2 π 1 --> 2 π 2 promień został wydłużony – fałsz
4) 2 π 1 --> π 2 promień widzimy jako wydłużony, ponieważ krzywizna uległa zmianie na ujemną - prawda.
W pierwszym przypadku gdy zmienia się geometria z 2 π 1 na 4 π ½, mamy do czynienia ze zwiększającą się krzywizną dodatnią, a w drugim gdy geometria zmienia się z 2 π 1 --> π 2 mamy do czynienia z krzywizną ujemną. Mamy wzór L = 2 π R, z którego wynika stosunek L/R = 2 π dla okręgu w stanie o krzywiźnie k = 1. Dla okręgu w stanie o krzywiźnie dodatniej będzie inaczej: L/R < 2 π. Dla okręgu w stanie o krzywiźnie ujemnej jeszcze inaczej: L/R> 2 π.
Stany fazowe i turbulencyjne okręgu.
Momenty przejść od jednego stanu liniowego – fazowego do innego stanu liniowego – fazowego możemy nazwać stanami turbulentnych przejść międzyfazowych. W przykładzie z gumką, stan taki pojawia się w trakcie skręcania jej od pojedyńczego okręgu do podwójnego, potrójnego itd. W tych stanach równowaga promieni okręgów składowych pod-promieni (wektorów) okręgu nie jest taka sama, jak w stanach fazowych, lecz jest zróżnicowana. W przypadkach stanów turbulencyjnych możemy je opisać na przykład przy pomocy dwóch okręgów, jeden zawarty w drugim o różnych promieniach i obwodach: rys.10
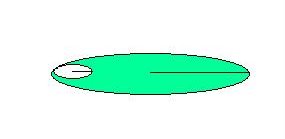
Okrąg zmienił stan w wymiarze krzywizny i w nowym stanie zamiast jednego pojawiły się dwa o różnym promieniu, w ten sposób, że wewnątrz jednego okręgu pojawiła się pętla w formie drugiego okręgu. Suma pod-promieni (wektorów) obu pod-okręgów składa się na stałą wartość promienia okręgu: r1 + r2 = R. Tak oto możemy zaobserwować na płaszczyżnie euklidesowej, że obwód L = 2 pi 1 został skrócony z powodu zmiany krzywizny. A promienie dwóch okręgów stanowią wartości ułamkowe ich suma jest równa jeden (1). Zmiany obwodu w wymiarze kołowym możemy też przedstawić za pomocą modelu orbifoldu. Całe koło to model superpozycji wszystkich stanów okręgu. Rys.11
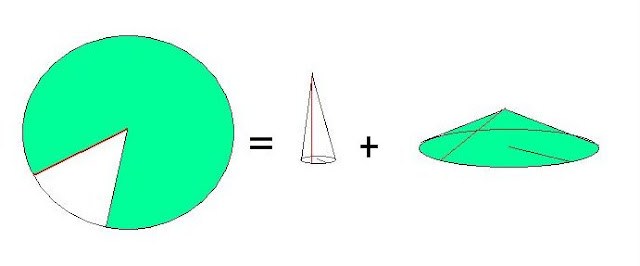
Podstawa białego stożka odpowiada brakującej części obwodu, która oczywiście istnieje w wyższej wymiarowości. Tu wyraźnie widać, że skrócenie promienia następuje z powodu wzrostu krzywizny dodatniej ( stożki z prawej). Wysokość stożka odpowiada wartości krzywizny. Ten model prowadzi nas do następnego sposobu opisania zmiany stanu okręgu. Teraz zamiast dwóch okręgów:

Mamy dwa stożki: rys.12
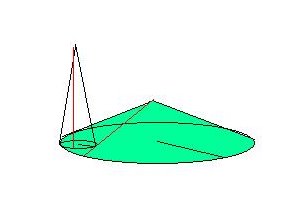
W podobny sposób opisaliśmy jeden ze stanów turbulentnego przejścia międzyfazowego. Podobnie możemy opisać stany fazowe – liniowe jako nakładające się na siebie stożki. Rys.13
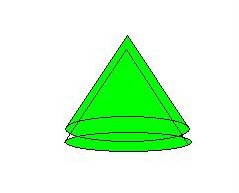
Tu dla podstawy stożka: L = 4 Pi r
Mniej więcej tak, jak na rysunku poniżej – w uproszczonym modelu - może wyglądać obserwowalny obraz świata cząstek energiomaterii poziomu kwantowego! Rys 12 i 13. Możemy teraz zaobserwować występowanie chwilowych efektów wzmocnienia stanów fazowych (stożki powielone) względem stanów turbulencyjnych. Na rysunku 13 i 14 poniżej mamy przedstawione dwa kolejne stany fazowe.
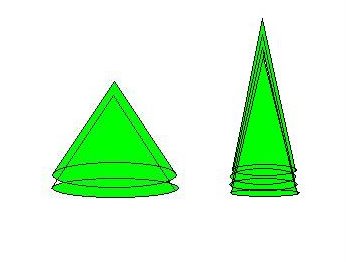
Tu: L = 4 Pi r dla podstawy stożka po lewej oraz L= 8 Pi r dla podstawy stożka po prawej.
Przypomnijmy sobie stany gumki skręconej do dwóch, trzech, czterech okręgów oraz stany gumki w trakcie skręcania czyli w ruchu. W pierwszym przypadku gumka znajdowała się w „fazach”, a w drugim w „przejściu międzyfazowym”. Okręgi w fazach są wzmocnione. Wytyczają orbity w polu grawitacyjnym. Im bardziej stają się wzmocnione tym większe prawdopodobieństwo znalezienia cząstki na orbicie. Na marginesie chcę przypomnieć, że obwód okręgu jest orbitą obiektu punktowego. Gdy uwzględnimy teraz wymiar czasu, możemy obwód utożsamić z prędkością punktu na orbicie. W ten sposób możliwa staje się obserwacja zmiany prędkości obiektu punktowego na zmiennych orbitach w polu grawitacyjnym. Zmiana orbit obiektów punktowych jest związana ze zmianami stanów (geometrii) okręgu związanymi ze zmianą wartości przyjmowanej w wymiarze krzywizny.
Wiedzieliśmy dotychczas, że :” koło na powierzchni kuli ma mniejszy obwód niż koło wykreślone na kartce papieru (powierzchni euklidesowej). A większy obwód będzie miało narysowane na powierzchni siodła”. Dotychczasowe wyjaśnianie, czym jest krzywizna było niepełne i nie wyjaśniało prawdziwej natury wymiaru krzywizny. Kontynuacja problemu pojawi się w części p.t:. Zgodność modelu Grawitora z OTW.
Różne stany orbit cząstek punktowych
Na euklidesowej płaszczyźnie odniesienia o zerowej krzywiźnie mamy teraz dwa okręgi A i B o różnych promieniach i obwodach, bo pomijamy sferę jako płaszczyznę odniesienia o innej krzywiźnie – ujednolicamy w ten sposób płaszczyznę odniesienia dla obiektu i obserwatora. Rys.15
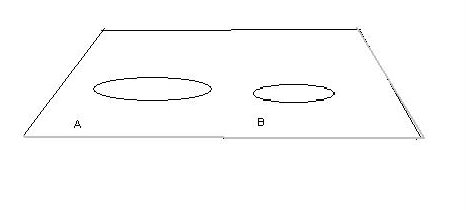
Okręgi przedstawiają dwa stany A i B meta-okręgu. Są to dwa stany tej samej figury, tego samego obiektu. Oba stany różni wielkość promienia i obwodu. Zrzutowanie meta-okręgu znajdującego się na powierzchni kuli jako stan B na płaszczyznę euklidesową spowodowało, że obserwujemy zmianę: obserwujemy inny okrąg (o proporcjonalnie mniejszym promieniu i obwodzie), który uległ odkształceniu do innego stanu. We wstępie pisałam, że odwrotność promienia to miara zakrzywienia okręgu czyli okrąg w stanie B ma zmienioną krzywiznę. Możemy teraz powiedzieć, że zmianie ulega krzywizna przestrzenna okręgu, a im mniejszy kolejny okrąg, tym większa staje się krzywizna dodatnia tego odkształcenia. Tę zmianę możemy uwzględnić właśnie dlatego, że parametry obwodu „L” i promienia „r” na płaszczyźnie euklidesowej są zmiennymi, które w wyższej wymiarowości mogą nie ulegają zmianie.
W wyższej wymiarowości ( w przestrzeni 3D) zmiana stanu A na stan B meta-okręgu nie powoduje zmiany promienia ani obwodu tylko zmianę jego kształtu. Ale my możemy to zaobserwować na płaszczyżnie euklidesowej jako zmianę krzywizny. Jeśli przyjmiemy, że zmienną ukrytą zależną od wymiaru krzywizny jest obwód, dokonamy innych obserwacji niż wówczas, gdy założymy, że zmienną ukrytą zależną od wymiaru krzywizny jest promień okręgu.
Proponowany przeze mnie nowy wzór L = k * π 2 R/n uwzględnia zmienność krzywizny stanów zachodzącą w wyższej wymiarowości. Dzięki zastosowaniu tego wzoru zmienność ta może być obserwowalna na płaszczyźnie euklidesowej. I to jest jeden z podstawowych powodów konieczności wprowadzenia dodatkowego wymiaru krzywizny kołowej.
Gdy wyróżnimy stan A okręgu, to do niego stosujemy wzór L = π 2R. Wówczas stan B względem stanu A będzie stanem o zwiększonej krzywiźnie dodatniej, Wiemy to, dzięki zastosowaniu wzoru L = k x π 2R/n (uwzględniającego zmianę krzywizny). Możemy jednak nie wiedzieć, jakie są zmienne ukryte. Wtedy wystarczy wyróżnić jeden ze stanów, na przykład stan B względem stanu A i stanowi B przypisać krzywiznę k = 1 i jego promieniowi przypisac wartość jednostkową R = 1. Wtedy stosując wzór L = k x π 2R/n zaobserwujemy stan A jako stan o ujemnej krzywiźnie względem stanu B o krzywiźnie zerowej. Taka obserwacja nie pomija rzeczywistych zmian przestrzennych figury zachodzących w dodatkowych wymiarach. Płaszczyzna odniesienia w powyższym rozumowaniu pozostaje ta sama, jednorodna, jeśli tylko zastosujemy wzór, który uwzględnia zmienność zachodzącą w wyższych wymiarach za pomoca wymiary - pojęcia krzywizny.
Okazuje się, że na euklidesowej płaszczyźnie odniesienia możliwe jest dokonywanie obserwacji nie tylko różnych okręgów, lecz także zmiennych stanów jednego i tego samego okręgu, ale tylko wtedy, gdy zastosujemy ubezwzględnienie jednego ze stanów względem innych przez przyrównanie wartości promienia R do jedności czyli R = 1. Rys.16
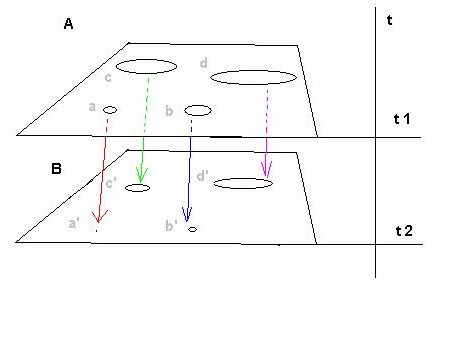
Na powyższym rysunku widać, że krzywizna okręgów ulega zmianie w czasie t. Co stało się z okręgami, które zmieniły stany i przeszły od stanów na płaszczyźnie A do stanów na płaszczyźnie B? Ulegają oddziaływaniom w jakiejś Metaprzestrzeni czyli próżni wypełnionej wirtualnymi cząsteczkami? Tak. Metaprzestrzeni w świecie fizycznym odpowiada próżnia wypełniona wirtualnymi cząstkami, które przejawiają się w naszym fizycznym świecie w momencie dokonywania obserwacji (przeprowadzania eksperymentów).
Uwzględniając wymiar czasu, możemy teraz wartość promienia przyrównać do stałej prędkości światła R = c. Z tego powodu do obserwacji „naszego fizycznego świata” założenie stałej prędkości „c” jest konieczne, ponieważ dzięki niemu możemy obserwować ten „nasz fizyczny świat”, a zwłaszcza cząstki poruszające się z różnymi prędkościami i "posiadającymi" różną masę.
Dualizm kwantowego świata
Dualizm korpuskularno-falowy jest po prostu dualizmem obserwacyjnym. Wynika z dwóch różnych sposobów prowadzenia obserwacji tego samego obiektu. Mamy dwa sposoby obserwacji okręgów. Rys 17
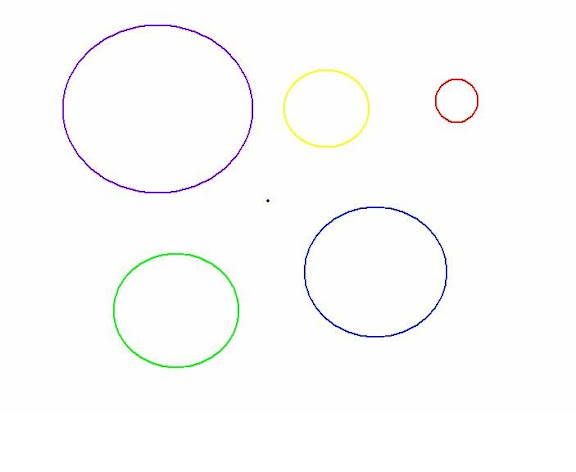
1. Te wszystkie okręgi możemy uznać za różne okręgi, pod warunkiem, że przypisujemy im krzywiznę zerową - określamy w ten sposób poziom klasyczny obserwacji.
2. Te wszystkie okręgi oraz punkt możemy uznać za różne stany jednego i tego samego okręgu o zmiennej krzywiźnie – w ten sposób określamy kwantowy sposób obserwacji.
W wymiarze krzywizny możliwa jest taka transformacja okręgu że mogą one zostać sprowadzone do stanu, który możemy określić jako punkt materialny. Rys.18
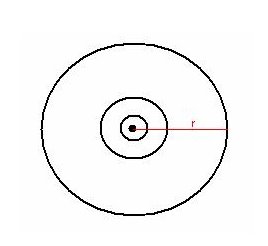
Każdy okrąg jest geodezyjną na sferze (powierzchni kuli), stą mamy wzór dla sfery: P(G) = k • 4 π R²/n, a dla okręgu: L (g) = k • π 2 R/n = k x 2 Pi r. Wyraz "P(G)" oznacza w tym przypadku powierzchnię pola grawitacyjnego, a "L(g)" oznacza w tym przypadku orbitę cząstki punktowej w polu grawitacyjnym.
Zatem im mniejszy promień pod-okręgu względem wyróżnionego okręgu uznanego za ubezwzględniony, tym większa jego krzywizna dodatnia, a im większy promień promień pod-okręgu względem ubezwzględnionego, tym większa jego krzywizna ujemna. Podokręgi nie mają "krzywizny zerowej". Taką krzywizną charakteryzuje się wyłącznie płaszczyzna euklidesowa.
TEZA III
1.Okręgio różnych obwodach i promieniach mogą być częściami jednego i tego samego meta-okręgu. Nazwiemy je wówczas pod-okręgami. Podobnie cząstki energetyczne są cząstkami jednej meta- cząstki znajdującej się w różnych stanach i w ten sposób przejawiąjącej się jako różne cząstki. Jednak dla rozpoznania tych różnych stanów należy dokonać wyróżnienia - ubezwzględnienia jednego ze stanów - jednego z okręgów. Tak, jak na przykład dokonujemy ubezwzględnienia wobec cząstki zwanej fotonem.
2.Nowy wzór L = k * 2π R/n za pomocą krzywizny przestrzennej pozwala na rozpoznawanie na płaszczyźnie euklidesowej różnych stanów meta-okręgu spowodowanych zmiennością jego kształtu w przestrzeni euklidesowej. Ten proces kwantowania czyli uwzględnienia zmiany wymiarowości obiektu opisuje użycie liczby „k” we wzorze L = k * 2π R/n.
3.Stan wyróżniony – ubezwzględniony wyznacza poziom krzywizny k =1 dla R =1 meta-okręgu, a jego stany względne wyznaczają różne poziomy na skali wymiaru krzywizny przestrzennej. Taka operacja wymaga przyjęcia pewnej długości promienia za stałą lub przyjęcia danego obwodu okręgu za stały.
Z powyższych tez wynika dodatkowa definicja :
Krzywizna wielu coraz mniejszych okręgów, może wzrosnąć do pewnego maksimum, wówczas obwody wszystkich takich okręgów stają się małymi kulkami czyli obiektami (cząstkami) punktowymi.
Geodezyjne a kwantowa geometria
Geodezyjne mogą określać zarówno stan ośrodka, próżni, jak i cząstek (obiektów) w nim/ w niej się przejawiających, poprzez uwzględnienie zróżnicowanej krzywizny. Potrzebny jest tu wymiar krzywizny. Prosty przykład: jeśli mamy okrąg o promieniu R, i ten okrąg ubezwzględniamy wobec innych (na przykład przyrównując r do stałej wielkości jednostkowej R = 1), wówczas okrąg o promieniu mniejszym niż 1 będzie charakteryzował się krzywizną dodatnią, a okrąg o promieniu większym niż 1 będzie charakteryzował się krzywizną ujemną.
Inaczej, można uwzględnić jeszcze wymiar czasu i ubezwzględnić promień geodezyjnej nadając mu wartość stałej prędkości światła R = c. Wszystki prędkości mniejsze c, będą prędkościami o dodatniej krzywiżnie, wszystkie większe od c będą prędkościami o krzywiznie ujemnej. Wszystkie prędkości różne od "c' będą wynikały ze zmiennej krzywizny przestrzennej orbit i trajektorii cząstek. Ich masa zaś będzie wynikiem geometrii ich pola grawitacyjnego. Ruch cząstek jako pęd, który jest wielkością wektorową, wynika z geometrii stałego lub zmiennego pola, w jakim dana cząstka się znaduje.
Ośrodek, w którym znajduje się cząstka, charakteryzuje się krzywizną ujemną (cząstki witrualne wypełniające próżnię), a cząstki w nim się przejawiające (cząstki traktowane jako cząstki materii) charakteryzują się krzywizną dodatnią.
A co z krzywizną zerową świata Płasków i euklidesową płaszczyzną?
Krzywizna zerowa występuje wyłącznie na granicy pomiędzy ośrodkiem a cząsteczkami (obiektami) znajdującymi się w trakcie obserwacji (eksperymentu). Sam obserwator zazwyczaj znajduje się na tej płaszczyżnie o krzywiżnie zerowej czyli euklidesowej płaszczyznie (stąd twierdzenia, że nasz świat jest płaski). W mistycznych doświadczeniach bywa inaczej, ale ten fakt na razie pominę.
ciąg dalszy być może nastąpi...

" Rzeczywistość składa się z nieskończonego strumienia interpretacji postrzegania, które my, jednostki posiadające specyficzne członkostwo nauczyliśmy się odczuwać jako oczywiste. (...) Nasz odbiór rzeczywistości jest przez nas uznawany za tak niepodważalny, że podstawowe założenie magii traktujące go jedynie jako jeden z wielu opisów, niełatwo przyjąć poważnie."
" Don Juan - człowiek wiedzy i nauczyciel Carlosa Castanedy. -------------------------------------------------
dodatek z dnia 13.09.09
"Każdy człowiek tworzy swoją osobistą historię ze swojej własnej i jedynej w swoim rodzaju perspektywy. Po co w takim razie narzucać innym swoją wersję, jeśli będzie ona dla nich nieprawdziwa? Kiedy to zrozumiesz, nie będziesz odczuwać potrzeby obrony tego, w co wierzysz. Nie jest ważne to, aby mieć rację i dowieść innym, że są w błędzie. Postrzegaj każdego człowieka jako ARTYSTĘ, kogoś, kto ma ci do opowiedzenia jakąś historię. Wiedz, że to, w co wierzą inni, jest po prostu ich punktem widzenia, i że nie ma to z Tobą nic wspólnego." Don Miguel Ruiz
-------------------------------------------------
--------------------------------------------------
Moje notki "unifikacyjne":
1. Geometria kwantowa 1
2. Geometria kwantowa 2
3. Geometria Kwantowa 3 -wstęp do kwantowej grawitacji
4. Geometria kwantowa 4
5. Torusy
6. Prędkość grawitacyjna a stała Plancka
7. Kwanty światła i eter - część I.
8. Kwanty światła i eter - część II.
pozostałe notki w polecane strony
Nowości od blogera
Inne tematy w dziale Technologie

