Wektor momentu pędu dla pojedynczego punktu to: wynik iloczynu wektorowego wektora położenia na wektor pędu względem środka ciężkości jakiegoś układu, którego ten punkt jest elementem.
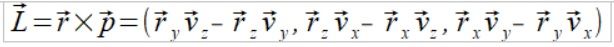
(1)
Jednak ludzki umysł nie jest na tyle bystry aby widzieć w równaniu (1) jakiś głębszy sens a wręcz intuicyjnie można dojść do wniosku że to jakieś przypadkowe relacje między sześcioma zmiennymi, które są ale nie mają jakiegoś głębszego sensu. Jednak w przyrodzie nic nie jest dziełem przypadku, nie ma zbędnych elementów a wszystko ma swój sens i ma swoje znaczenie w perfekcyjnej harmonii reguł Fizycznych jakie nas otaczają. A harmonię ta opisuje matematyka która jest idealnym odbiciem otaczającej nas rzeczywistości.
Podjąłem się ciężkiej pracy odkrywania tej harmonii ponieważ uwierzyłem w tą perfekcje przyrody i po odkryciu jednego prawdziwego elementu, wiedziałem że pozwoli mi on na odnajdywania kolejnych elementów łańcucha przyczynowo skutkowego do momentu aż pokaże mi się całe piękno tego mechanizmu. Na początku wiedziałem że skoro wektor prędkości kątowej ciała sztywnego zmienia swoją pozycje w czasie, to jest to przyspieszenie kątowe a przyspieszenie kątowe jest efektem działania momentu siły, czyli podczas obrotu ciał sztywnych, wewnątrz muszą być siły odpowiedzialne za to i prawdę mówiąc nic wiele więcej nie wiedziałem:) Niestety w książkach nic o tym nie ma a każdy Fizyk dałby sobie głowę uciąć że to niemożliwe.
Uprośćmy więc wzór (1) do zjadliwej postaci gdzie każdy kto ma jakie takie pojęcie o matematyce będzie mógł ją zrozumieć. Zacznijmy od tego że wektor pędu to pochodna wektora położenia razy jego masa i od teraz wiemy że wektor momentu pędu nie jest złożony z dwóch różnych wektorów a z wektora położenia i jego pochodnej razy masa która przyjmijmy że jest stała.
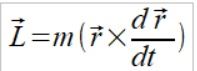
(1.a)
Jest taka własność przestrzeni że: dla każdych dwóch dowolnych wektorów A i B można znaleźć taki układ odniesienia w którym wektory te znajdują się na jednej płaszczyźnie IJ i jeden z tych wektorów A możemy umieścić na jednej z osi głównej tego układu a wektor będący wynikiem iloczynu wektorowego tych wektorów A x B =C znajdować się będzie na osi prostopadłej do płaszczyzny IJ którą tworzą
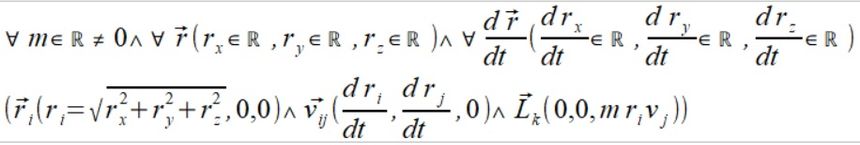
Jest też taka własność iloczynu wektorowego że: wektor C będący jego wynikiem składa się z wartości jednego wektora A razy wartość składowej prostopadłej drugiego wektora B. Czyli dla dowolnej chwili, zawsze możemy zapisać wektor momentu pędu jako iloczyn wektorowy wektora położenia na składową prostopadłą pierwszej pochodnej wektora położenia razy masa. W ten sposób uzyskujemy dużo prostszą postać momentu pędu jako równanie.
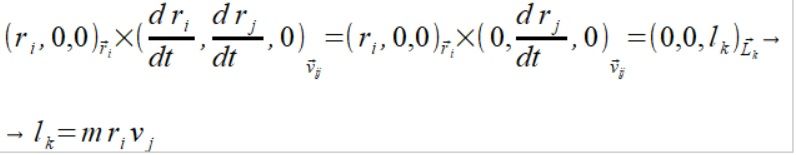
(1.b)
Sprowadziliśmy wektor momentu pędu do równania co nam bardzo upraszcza zrozumienie czym on jest ale musimy teraz bardzo ostrożnie je przekształcać, pamiętając że wciąż są to wektory i nie każde przekształcenie tego równania jest tożsame z przekształceniem tych wektorów.
W iloczynie wektorowym (1.b) pominęliśmy wartość dri/dt gdyż ta wartość jest nieistotna dla wektora momentu pędu L_k w tej konkretnej chwili i równanie ją ignoruje. Jednak czy w przyrodzie może być jakiś element który nie ma znaczenia, jest bezwartościowy? Czy matematyka powoduje że element ten przepada? Nie ma tu przypadku jak i nie ma elementów zbędnych które nic nie znaczą a równanie jest perfekcyjnie doskonałe, opisujące perfekcyjną harmonię otaczającej nas rzeczywistości.
Pamiętając że w rzeczywistości dt musi być różne od zera, policzmy jak wyglądałby wektor momentu pędu gdy dokona się jakaś zmiana wektora położenia wzdłuż tego wektora czyli nasze zaginione dri/dt , przy niezmiennym drj/dt w konkretnej chwili t1 dla ruchu płaskiego
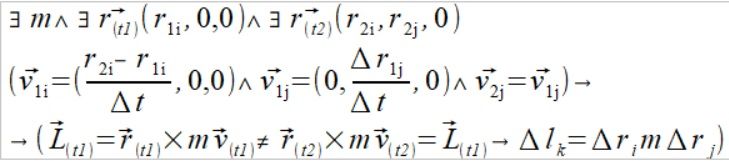
(2)
Jak widać w tezie (2), występowanie pierwszej pochodnej wektora położenia wzdłuż tego wektora dr1i (to nie to samo co druga pochodna czyli wektor przyspieszenia dośrodkowego) przy stałym wektorze prędkości dr1j=dr2j musi skutkować zmianą wektora momentu pędu. Można więc postawić konkluzje że sama zmiana wartości wektora położenia (zmiana momentu bezwładności) skutkuje zmianą wektora momentu pędu. Dla naszego przykładu jest to
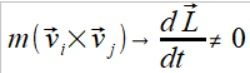
(3)
Na razie nie ma znaczenia czy mamy vj1 czy vj2 ponieważ w tym przykładzie wartości te są równe. Dla nowych czytelników równanie (3) jest kontynuacją wywodu który znajduje się (tutaj wzór (2)) oraz dowód poprawności znajduje się tutaj
Możemy łatwo dowieść że ta zmiana momentu pędu to wektor prędkości wzdłuż wektora położenia na wektor prędkości do niego prostopadły.
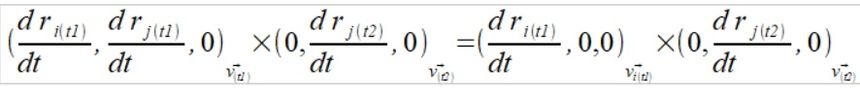
(4)
Jednak każdy kto interesuje się Fizyką wie że zmiana momentu bezwładności dri powoduje zmianę wartości prędkości drj. Możemy więc rozpisać taki schemat
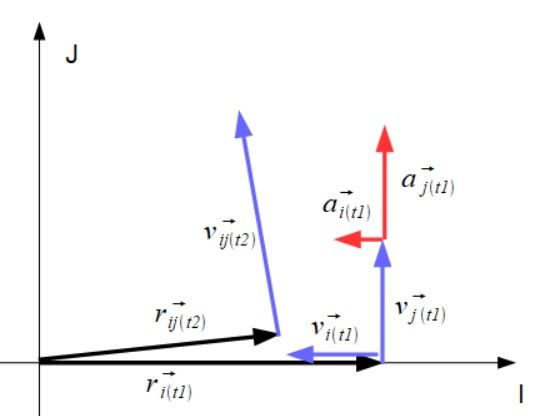
Ponieważ znów sprawa się trochę skomplikowała, dokonajmy kolejnego uproszczenia przechodząc do jeszcze innego układu odniesienia gdzie wektor położenia zostanie unieruchomiony na jednej z osi i wtedy znika przyspieszenie na osi I
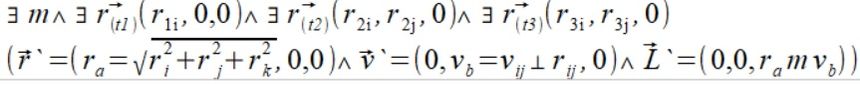
(5)
Mamy teraz bardzo prostą geometryczną wizualizacje jak zmienia się wektor momentu pędu dla ruchu na płaszczyźnie.
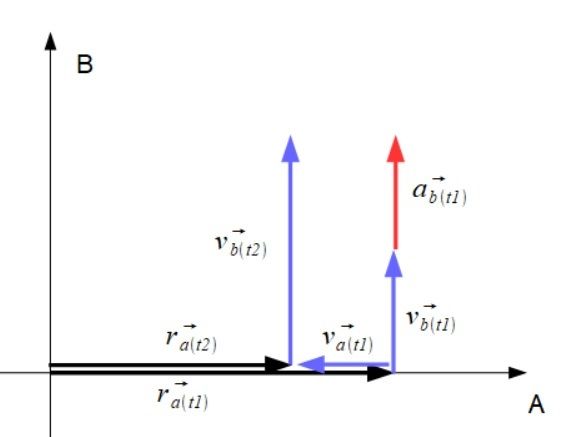
Możemy teraz na bazie zasady zachowania momentu pędu wyliczyć pochodną wektora momentu pędu
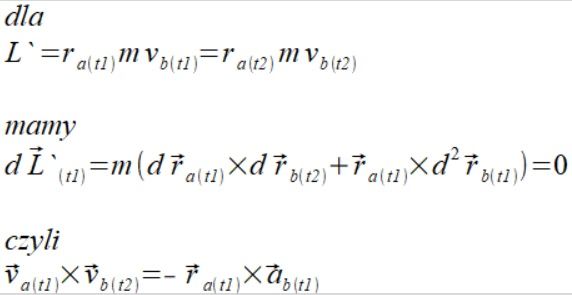
(6)
Moja interpretacja (6) jest taka że: zmiana momentu bezwładności wywołuje zmianę momentu pędu oraz powstanie wewnętrznego momentu siły który tą zmianę rekompensuje.
Niektórzy starają się minimalizować znaczenie moich wyników argumentując że tak na prawdę one nic nie zmieniają, co nie jest prawdą. Otóż zmieniają one rozumienie mechaniki obrotu punktu i łamią błędne schematy. Do tej pory uważano (zresztą dalej się uważa) że odosobniony układ (na przykład ciało sztywne) nie ma możliwości wygenerowania niezerowego momentu siły i zakładano że taki niezerowy moment siły musiałby łamać dotychczasowo uznawane prawa Fizyki. Ja dowodzę że takie założenie jest błędne bo po pierwsze odosobniony układ może posiadać niezerowy moment siły a dodatkowo jest on niezbędny aby utrzymać obecnie uznawane prawa Fizyki.
Do tej pory nikt świadomie nie używał tych momentów siły ponieważ obecna nauka uważa je za nieistniejące i kiedy można by ich użyć, zastępowano to jakimś innym mechanizmem zewnętrznym a od teraz będzie można to zmienić.
Dlaczego nikt wcześniej tego nie znalazł? Ponieważ nikt tego nie szukał, bo po co szukać czegoś czego nie ma?
Notka stała się bardzo długa a jeszcze trzeba by omówić zmianę wektora położenia wzdłuż wektora momentu pędu z którymi mamy do czynienia przy obrocie ciała sztywnego ale strasznie by to wydłużyło tekst. Dlatego może skończę tutaj a zmiany wzdłuż wektora momentu pędu opisze w następnej notce.
Inne tematy w dziale Technologie

