„Każdy głupi może wiedzieć, sedno to zrozumieć”
Einstein
Tensor momentu bezwładności pierwsze starcie. Umiem go liczyć ale wciąż nie umiem go zrozumieć. Mnożąc tensor przez wektor powstaje całkiem nowy wektor ale dlaczego taki a nie inny? Działa ale ja nie umiem pojąć jego mechanizmu działania, przynajmniej na razie.
Magia tensora
L=Ĩω (1)
Jak to się liczy pokazuje poniższa prezentacja
http://home.agh.edu.pl/~zak/downloads/Bryla%20sztywna.pdf
Mamy więc takie równania
Lx=Ixxωx+Ixyωy+Ixzωz (2)
Ly=Iyxωx+Iyyωy+Iyzωz
Lz=Izxωx+Izyωy+Izzωz
Co ciekawe używając tensora aby utrzymać prawo zachowania krętu dozwolony jest tylko jeden specjalny układ odniesienia z trzema głównymi momentami bezwładności gdzie osie te pokrywają się z osiami głównymi układu.
Mamy wtedy przykładowo taki tensor
Ixx=2; Ixy=0; Ixz=0; (a)
Iyx=0; Iyy=4; Iyz=0;
Izx=0; Izy=0; Izz=6;
W przypadku tym pozadiagonalne wartości które są też nazywane momentami dewiacji są równe zero. Mając teraz na przykład taką prędkość kątową ω(x,0,0) podstawiając tensor (a) do wzoru (2) otrzymamy taki moment pędu
Lx=Ixxωx+0+0=Ixωx
Ly=0+0+0
Lz=0+0+0
Jeżeli podstawimy omegę która nie leży na osi głównej ω(x,y,0) otrzymamy
Lx=Ixxωx+0+0=Ixωx
Ly=0+Iyyωy+0=Iyωy
Lz=0+0+0
Jeżeli obrócimy teraz układ odniesienia o jakiś kąt wzdłuż osi z momenty dewiacji Ixy, Iyx przestaną być zerowe oraz Ix≠Ixx i Iy≠Iyy
Lx=Ixxωx+Ixyωy+0
Ly=Iyxωx+Iyyω+0
Lz=0+0+0
Momenty dewiacyjne mają skutkować zmianą wektora krętu w czasie dL/dt≠0. Jak to działa? dokładnie tego jeszcze nie wiem.
Zaczynam się wgryzać w tensor następująco. Sprawdziłem działanie tensora na jednym punkcie, co częściowo potwierdziło moje przypuszczenia.
Uwaga
Gdy mamy do czynienia z pojedynczym punktem posiadający wektor v na który działa siła dośrodkowa, wektor ω będzie zawsze prostopadły do działającej siły i wektora pędu. W przypadku tym wektor krętu L będzie również prostopadły do ramienia i pędu czyli wektory ω i L będą do siebie równoległe.
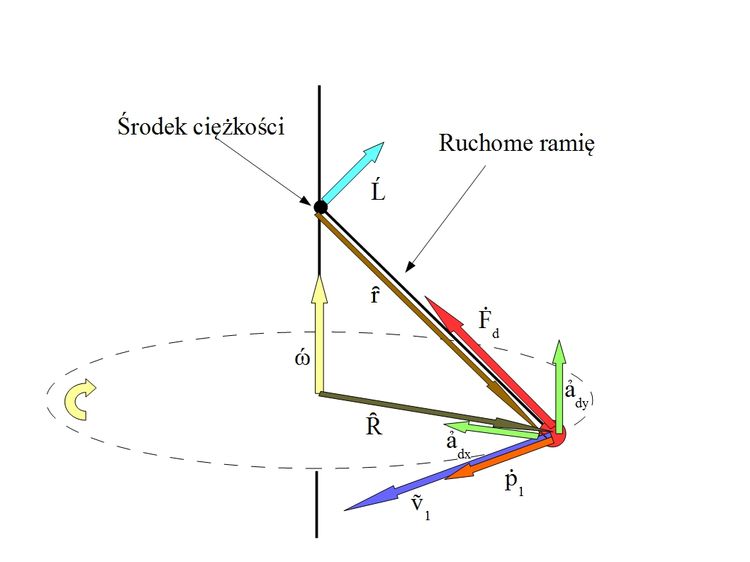
Z sytuacją kiedy ω i L nie są do siebie prostopadłe mamy do czynienia w szczególnym przypadku obrotu bryły sztywnej BS, gdzie punkty tej bryły nie mogą się względem siebie przemieszczać. Wirtualnie wyciągam jeden punkt z bryły i sztucznie ustalam wektor prędkości kątowej ω symulujący wektor prędkości kątowej BS.
Jak wyliczać chwilowe osie obrotu dla dwóch punktów bryły sztywnej pokazuje poniższy link.
http://home.agh.edu.pl/~wslosar/18.htm
W animacji prezentowanej poniżej w pierwszej kolejności użyłem jednego punktu m=1 na ramieniu r=1 i obracałem go po trochę o 180 stopni wokół osi z. Sztucznie zatrzymałem wektor prędkości kątowej w pozycji ω(1,0,0). W każdej pozycji liczyłem tensor bezwładności dla tego punktu i za pomocą wzoru (2) wyliczałem wektor krętu L. Niespodzianki nie było wektor L zawsze ustawia się prostopadle do ramienia a jego długość maleje im bliżej punkt jest osi obrotu.
L= r x p
v= ω x r
Czyli im mniejsza odległość do osi obrotu tym mniejsze L.
Następnym krokiem było za symulowanie dwóch prostopadłych do siebie punktów o tej samej masie.
m1(1,0,0)=1; m2(0,1,0)=1
Jak się okazała w takim przypadku kręt L jest stały w czasie i równoległy do ω
Następnie sprawdziłem dwa prostopadłe do siebie punkty o różnych masach.
m1(1,0,0)=1; m2(0,1,0)=2
Kręt nie jest już równoległy do ω i nie jest już stały w czasie obrotu mas wokół osi z. Sprawdziłem teraz jak będą wyglądać siły dośrodkowe gdy utworzymy je zgodnie z obecnie stosowaną metodą. Wzór na siłę dośrodkową to
Fd=mω^2r┴
Przy czym r┴ jest to składowa promienia prostopadła do osi obrotu, jednocześnie siły te skierowałem prostopadle do ω a następnie je zsumowałem uzyskując wypadkową sił F. Następnie dokonałem iloczynu skalarnego F x L i bez zaskoczenia z całą pewnością mogę stwierdzić że uzyskany wynik ewidentnie nie jest zerowy. Wiedząc że
dL/dt= r x F
Tak działające siły musiały by skutkować złamaniem prawa zachowania momentu pędu.
Nowa metoda
Siłę dośrodkową wyliczamy z tego samego wzoru
Fd=mω^2r┴
Jednak kierujemy je do środka ciężkości. Symuluje takie siły i wyliczam sumę ich działania, wypadkową tych sił F. Licząc iloczyn skalarny F x L wychodzą wyniki 10^-15 wynikające zapewne wad symulatora, można to uznać za zero. Tak działające siły nie skutkują zmianą wektora krętu są one dla niego neutralne.
https://youtu.be/hnR9L3AvVPk
To już nie jest gdybanie a matematyczny model jednoznacznie weryfikujący błędność obecnej interpretacji sił dośrodkowych i potwierdzające moje założenia.
To już nie jest intuicja a fakt naukowy.
Jeszcze o momentach sił. Kiedy na wektor pędu działa siła do niego prostopadła to efektem działania takiej siły jest zmiana kierunku wektora pędu jednocześnie nie zmienia się jego wartość. Siła taka zwana dośrodkową nie skutkuje wykonaniem pracy czyli zmianą energii.
https://pl.wikipedia.org/wiki/Si%C5%82a_do%C5%9Brodkowa
Czyli jeżeli mamy pęd (x,0,0) to siły skierowane do niego prostopadle nie skutkują wykonaniem pracy, jest to Fy(0,y,0) i Fz(0,0,z). Jedynie Fx(1,0,0) jest siłą wykonującą prace. Mając teraz promień r(0,y,0) tworzy on z wektorem pędu wektor krętu L= r x p w naszym przypadku L(0,0,z). Znaczy to że moment siły Mx (x,0,0) wywołany siłą Fz(0,0,z) jest momentem siły nieefektywnym.
Kod do metody z Fd skierowanymi wzdłuż ramienia
from visual import *
m1=1
m2=2
x1=1
y1=0
z=0
x2=0
y2=1
W=vector(1,0,0)
omega=1
print omega
TIxx=(m1*((y1*y1)+(z*z)))+(m2*((y2*y2)+(z*z)))
TIyy=(m1*((x1*x1)+(z*z)))+(m2*((x2*x2)+(z*z)))
TIzz=(m1*((x1*x1)+(y1*y1)))+(m2*((x2*x2)+(y2*y2)))
TIxy=(m1*x1*y1)+(m2*x2*y2)
TIxz=(m1*x1*z)+(m2*x2*z)
TIyx=(m1*y1*x1)+(m2*y2*x2)
TIyz=(m1*y1*z)+(m2*y2*z)
TIzx=(m1*z*x1)+(m2*z*x2)
TIzy=(m1*z*y1)+(m2*z*y2)
Fd1=m1*omega*omega*y1
Fd2=m2*omega*omega*y2
print "F", Fd1,Fd2
L=vector((W.x*TIxx-W.y*TIxy-W.z*TIxz),(-W.x*TIyx+W.y*TIyy-W.z*TIyz),(-W.x*TIzx-W.y*TIzy+W.z*TIzz))
print "W",W
omega=arrow(axis=vector(W.x,W.y,0), color= color.blue, shaftwidth=0.05)
kret=arrow(axis=vector(0,0,0), color= color.red, shaftwidth=0.04)
promien1=arrow(axis=vector(x1,y1,0), color= color.yellow, shaftwidth=0.01)
promien2=arrow(axis=vector(x2,y2,0), color= color.yellow, shaftwidth=0.01)
masa1=sphere(pos=vector(x1,y1,0),radius=0.05)
masa2=sphere(pos=vector(x2,y2,0),radius=0.05)
sila1=arrow(pos=masa1.pos,axis=-vector(x1,y1,0)*Fd1, color= vector(0.5,1,0), shaftwidth=0.05)
sila2=arrow(pos=masa2.pos,axis=-vector(x2,y2,0)*Fd2, color= vector(0.5,1,0), shaftwidth=0.05)
sumaF=arrow(axis=-vector(0,Fd1+Fd2,0), color= vector(1,0.5,0), shaftwidth=0.03)
t=0
while t<10:
rate(3)
x1=x1-0.1
y1=sqrt(1-(x1*x1))
y2=y2-0.1
x2=-sqrt(1-(y2*y2))
# r1=sqrt((x1*x1)+(y1*y1))
TIxx=(m1*((y1*y1)+(z*z)))+(m2*((y2*y2)+(z*z)))
TIyy=(m1*((x1*x1)+(z*z)))+(m2*((x2*x2)+(z*z)))
TIzz=(m1*((x1*x1)+(y1*y1)))+(m2*((x2*x2)+(y2*y2)))
TIxy=(m1*x1*y1)+(m2*x2*y2)
TIxz=(m1*x1*z)+(m2*x2*z)
TIyx=(m1*y1*x1)+(m2*y2*x2)
TIyz=(m1*y1*z)+(m2*y2*z)
TIzx=(m1*z*x1)+(m2*z*x2)
TIzy=(m1*z*y1)+(m2*z*y2)
L=vector((W.x*TIxx-W.y*TIxy-W.z*TIxz),(-W.x*TIyx+W.y*TIyy-W.z*TIyz),(-W.x*TIzx-W.y*TIzy+W.z*TIzz))
Fd1=m1*y1*1*1
Fd2=m2*sqrt(y2*y2)*1*1
kret.axis=vector(L.x,L.y,L.z+0.01)
promien1.axis=vector(x1,y1,0)
promien2.axis=vector(x2,y2,0)
masa1.pos=vector(x1,y1,0)
masa2.pos=vector(x2,y2,0)
sila1.pos=vector(x1,y1,0)
sila1.axis=-vector(x1,y1,0)*Fd1
sila2.pos=vector(x2,y2,0)
sila2.axis=-vector(x2,y2,0)*Fd2
sumaF.axis=sila1.axis+sila2.axis
LxF=sumaF.axis.x*L.x+sumaF.axis.y*L.y+sumaF.axis.z*L.z
print t,"L x F",LxF
t=t+1
Inne tematy w dziale Technologie

