W notce znajdują się wzory i ich opis, następnie przedstawiona jest animacja z wyników symulacji, oraz podany jest kod programu do wyliczenia poszczególnych wektorów.
Prawdziwego mężczyznę poznaje się nie po tym jak zaczyna a po tym jak kończy.
Zaczynałem na naprawdę niskim poziomie ale co chwilę podnoszę poprzeczkę. Wielu twierdzi że to o czym ja piszę jest znane od dawna i tylko moja niewiedza jest skutkiem tego że o tym nie słyszałem. Być może tak jest ale jak do tej pory stwierdzenia te są oparte na jakiejś wiedzy tajemnej, która przede mną jest ukrywana i niejako po złości nikt mi nie potrafi wskazać gdzie ta wiedza się znajduje. Ja do tej wiedzy dotrzeć nie potrafię i dlatego musiałem ją stworzyć od podstaw.
Kiedyś zapowiedziałem że nie skończę z tematem póki nie zrozumiem w pełni działania wszystkich wektorów podczas mechaniki obrotu BS. I jestem już blisko zakończenia tego etapu. Niestety zawsze jest jakieś ale, wszystko się domyka oprócz sił dośrodkowych których mam trzy wersje rozwiązania. Ale zacznijmy od początku.
Na początku trzeba dokładnie zrozumieć jak działają zależności podczas iloczynu wektorowego. Gdy mamy:
a x b = c
oraz osie do siebie prostopadłe
i ┴ j ┴ k
Ustalamy proporcje.
ck=ai*bj
ai=ck/bj
bj=ck/ai
I tutaj trzeba wprowadzić pojęcie odwrotności wektora. Pisałem o tym kilka notek temu i jak do tej pory nikt nie przedstawił żadnego argumentu przeciw. Odwrotność wektora jest to odwrotność wartości skalarnej na tym samym kierunku i zwrocie co wektor pierwotny.
a(ax,ay,az)=√(ax2+ay2+az2)
1/a=a/a2=(ax/a2, ay/a2, az/a2)
Przykłady odwrotności wektorów
d (1,1,1) 1/d (1/3, 1/3, 1/3)
e (1,1,0) 1/e (1/2, 1/2, 0)
f (1,0,0) 1/f (1,0,0)
Możemy teraz w prosty sposób rozpisać równania iloczynu wektorowego.
c = a x b
a = 1/b x c
b = c x 1/a
Znając te równania z łatwością rozpisujemy je dla wektorów prędkości v, położenia r, i prędkości kątowej ω. Są to prawdziwe zależności tych wektorów dla punktu swobodnego.
v = ω x r = 1/s * m
ω = 1/r x v = 1/m * m/s
r = v x 1/ω = m/s * s
Dla bryły sztywnej gdzie punkty nie mogą się swobodnie względem siebie poruszać nie powinno się tych wzorów stosować bezpośrednio. Ważne aby zrozumieć jak te wektory działają gdy punkty są ze sobą powiązane siłami więzów. Bryły sztywne które mają różne momenty bezwładności na osiach głównych mają tę cechę że bardzo trudno jest uzyskać podczas ich obrotu nieruchomy wektor prędkości kątowej ω. Podczas swobodnego obrotu takiej bryły, chociaż nie działa na ten układ żadna zewnętrzna siła to i tak wektor prędkości kątowej nie jest stały w czasie. Pokazuje to poniższa symulacja.
Jednak w każdej chwili istnieje chwilowa oś obrotu z chwilowym wektorem ω względem których wszystkie punkty BS się obracają. Co to znaczy? Oznacza to że w danej chwili wektor prędkości każdego punktu spełnia równanie
v = ω x r
Gdzie r jest to wektorem położenia względem chwilowej osi obrotu i do niej prostopadły.
Chwilowa oś obrotu jest to oś znajdująca się na kierunku chwilowego wektora ω.
Jak mając wektory położenia punktów i ich prędkości wyliczyć chwilową prędkość kątowa dla całej bryły sztywnej?
Mamy następującą BS:
m1x`(√2, √2, 0); v1(0,0,-2)
m2x`(-√2, -√2, 0); v2(0,0,2)
m3y`(-√2, √2, 0); v3(0,0,-2)
m4y`(√2, -√2, 0); v4(0,0,2)
Środek ciężkości jest środkiem zarówno inercjalnego jak i nieinercjalnego układu odniesienia.
m1, m2 znajdują się na osi głównej BS x`. m3,m4 znajdują się na osi głównej BS y`. Osie główne przecinają się w środku ciężkości. Wyliczmy prędkości kątowe względem środka układu dal osi głównych.
ωx`=(-√2/2, √2/2, 0)
ωy`=(-√2/2, -√2/2, 0)
Okazuje się że są to składowe chwilowego wektora prędkości kątowej
Ω = ωx` + ωy` =(√2, 0, 0)
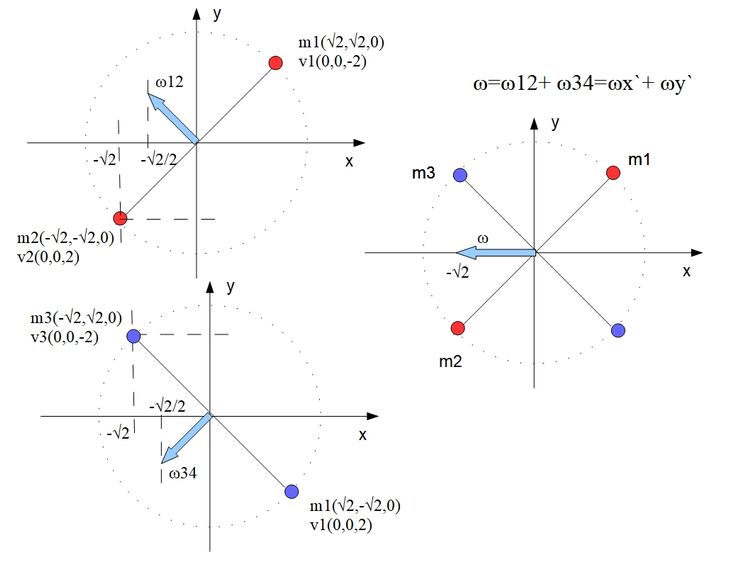
Jak łatwo policzyć wektor prędkości punktu BS znając jedynie wektor chwilowej prędkości kątowej i jego położenie? W tym przypadku trzeba znać pewną własność iloczynu wektorowego. Pseudowektorem c będącym wynikiem iloczynu wektorowego dwóch dowolnych wektorów a i b, jest wektor będący prostopadły do płaszczyzny na której leżą wektory a, b a jego wartość jest to iloczyn wartości tych wektorów a*b razy sinus kąta zawarty między nimi.
a x b = c ---> c=absinα
Jeżeli Ω (x,0,0) ma tylko składową x, natomiast wektor położenia r (x,y,0) to płaszczyzną tych dwóch wektorów jest płaszczyzna XY czyli wektor prędkości v będzie do tej płaszczyzna prostopadły i będzie miał współrzędne jedynie na osi z v(0,0,z). Natomiast wartość v jest to iloczyn wartości Ωx*ry.
ry┴Ω i rx║Ω
v = Ω x ry
Bardzo ważnym wektorem jest moment pędu potocznie zwany krętem. Dla swobodnego punktu jest to:
L = r x p
Zauważyłem że nie zawsze jest doprecyzowane czym w tym wzorze jesr r. To jakie weżmiemy r może zmienić wynik końcowy a nie może być tak że kręt zmienia się w zależności od układu odniesienia jaki weżmiemy do wyliczeń. Bardzo ważne aby zrozumieć że dla swobodnego punktu jest to prostopadła odległość do osi obrotu zgodnie ze wzorem v = ω x r dla punktu swobodnego, jednak dla BS jest to wektor położenia punktu względem środka ciężkości. Skąd o tym wiemy? Przy liczeniu Krętu L za pomocą tensora momentu bezwładności bierzemy współrzędne punktów względem środka ciężkości i to jest właśnie r we wzorze na L
Lx= ωxΣmn(rn2-xn2) + ωyΣmnxnyn + ωzΣmnxnzn
Ly= ωxΣmnynxn + ωyΣmn(rn2-yn2) + ωzΣmnynzn
Lz= ωxΣmnznxn + ωyΣmnznyn + ωzΣmn(rn2-zn2)
Kręt dla bryły sztywnej można wyliczyć o wiele prościej. Mamy trzy osie główne Ix, Iy, Iz. Można to przedstawić za pomocą modelu gdzie na każdej z osi mamy parę symetrycznych mas których suma momentów bezwładności daje Ix, Iy, Iz.
Ix=mxr2 + m-xr2; Iy=myr2=m-yr2
Wtedy
Lx = (r1 x p1)x + (r2 x p2)-x
Ly = (r3 x p3)y + (r4 x p4)-y
Lz = (r5 x p5)z + (r6 x p6)-z
L = Lx + Ly + Lz
Następnym wektorem jest przyspieszenie dośrodkowe ad dla punktu. Mamy dwa wzory na ad
ad=rω2 --> rω=v
ad=v2/r --> v/r=ω
ad=ωv
Wiemy że ad jest wektorem odwrotnym do wektora położenia
ad║-r
Można teraz łatwo ustalić wzory iloczynu wektorowego dla ad
ad = ω x v
ω = 1/v x ad
v =ad x 1/ω
Teraz z łatwością można wyliczyć chwilową prędkość kątową Ω za pomocą przyspieszeń dośrodkowych dla bryły sztywnej.
Ω=ωx`+ωy`+ωz`=(1/v x ad)x` + (1/v x ad)y` + (1/v x ad)z`
Idąc za ciosem można pokusić się o wyznaczenie sił dośrodkowych Fd. Niestety sprawa nie jest już taka prosta. Doszedłem do trzech różnych koncepcji dla Fd.
Wersja pierwsza.
F=am
ω = 1/v x ad
ω = 1/mv x mad
ω = 1/p x Fd
Fd = ω x p
p = Fd x 1/ω
Wersja druga
Ω = (x, 0, 0)
r = rx +ry = r┴ + r║
Fd=mω2 ry
Wersja trzecia
Ω = (x, 0, 0)
r = rx +ry = r┴ + r║
Fd=mω2 r
Fd=m(1/ry x v)2 r
Jak wyglądają te wersje oraz wszystkie powyższe wzory pokazuje animacja z symulacji.
Mam więc trzy wersje które trzeba poddać weryfikacji i porównać je ze wzorami Eulera i modelem wahadła stożkowego. Po zrozumieniu działania wektorów sił dośrodkowych nareszcie będzie można wyliczyć momenty sił jakie powodują i sprawdzić jak one się mają do mechaniki obrotu BS.
Kod do animacji
from visual import *
mx=0.5 #masy x`,y`
my=1.
x1=1 #pozycja m1,m2 na osi x`
y1=0
z1=0
x2=0 #pozycja m3,m4 na osi y`
y2=1
z2=0
r=vector(x1,y1,z1) #promien
R=mag(r)
#print R
W=vector(0.9,0,0) #omega
v1=W.x*y1 #predkosci
v2=W.x*-y1
v3=W.x*y2
v4=W.x*-y2
p1=mx*v1 #ped
p2=mx*v2
p3=my*v3
p4=my*v4
ax=(v1*v1) #przyspieszenia a=(v^2)/r; r=1
ay=(v3*v3)
#print "v",v1,v2,v3,v4
TIxx=(2*mx*((y1*y1)+(z1*z1)))+(2*my*((y2*y2)+(z2*z2))) #mx1 i mx2 --> 2*mx
TIyy=(2*mx*((x1*x1)+(z1*z1)))+(2*my*((x2*x2)+(z2*z2))) #elementy tensora
TIzz=(2*mx*((x1*x1)+(y1*y1)))+(2*my*((x2*x2)+(y2*y2)))
TIxy=(2*mx*x1*y1)+(2*my*x2*y2)
TIxz=(2*mx*x1*z1)+(2*my*x2*z2)
TIyx=(2*mx*y1*x1)+(2*my*y2*x2)
TIyz=(2*mx*y1*z1)+(2*my*y2*z2)
TIzx=(2*mx*z1*x1)+(2*my*z2*x2)
TIzy=(2*mx*z1*y1)+(2*my*z2*y2)
Fdx=mx*W.x*W.x*y1 #sily dosrodkowe na osiach glownych z Fd=mW^2ry
Fdy=my*W.x*W.x*y2
#print "F", Fd1,Fd2
Fdax=mx*ax #sily dosrodkowe na osiach glownych z F=ma
Fday=my*ay
#L=vector((W.x*TIxx-W.y*TIxy-W.z*TIxz),(-W.x*TIyx+W.y*TIyy-W.z*TIyz),(-W.x*TIzx-W.y*TIzy+W.z*TIzz))
#print "W",W
omega=arrow(axis=vector(W.x,W.y,0), color= color.blue, shaftwidth=0.05) #omega startowa
#kret=arrow(axis=vector(0,0,0), color= color.red, shaftwidth=0.04)
kret2=arrow(axis=vector(0,0,0),color=vector(1,0.4,0.4), shaftwidth=0.04)
#kret2x=arrow(axis=vector(0,0,0),color=vector(1,1,0.3), shaftwidth=0.04)
#kret2y=arrow(axis=vector(0,0,0),color=vector(1,1,0.3), shaftwidth=0.04)
dv1=arrow(axis=vector(0,0,0), color=vector(0.3,0.6,0), shaftwidth=0.05) #przyspieszenie punktow
dv2=arrow(axis=vector(0,0,0), color=vector(0.3,0.6,0), shaftwidth=0.05)
dv3=arrow(axis=vector(0,0,0), color=vector(0.3,0.6,0), shaftwidth=0.05)
dv4=arrow(axis=vector(0,0,0), color=vector(0.3,0.6,0), shaftwidth=0.05)
dvg=arrow(pos=vector(0,1,0),axis=vector(0,0,0), color=vector(0.6,0.6,0), shaftwidth=0.05)
dvd=arrow(pos=vector(0,-1,0),axis=vector(0,0,0), color=vector(0.6,0.6,0), shaftwidth=0.05)
#omegax=arrow(axis=vector(0,0,0), color= vector(0,0,0.01), shaftwidth=0.02)
#omegay=arrow(axis=vector(1,0,0), color= vector(0,0,0.01), shaftwidth=0.02)
masa1x=sphere(pos=vector(x1,y1,0),radius=0.05) #bryla sztywna
masa2x=sphere(pos=vector(-x1,-y1,0),radius=0.05)
masa1y=sphere(pos=vector(x2,y2,0),radius=0.05)
masa2y=sphere(pos=vector(-x2,-y2,0),radius=0.05)
promien1=arrow(pos=masa2x.pos, axis=masa1x.pos-masa2x.pos, color= color.yellow, shaftwidth=0.005)
promien2=arrow(pos=masa2y.pos, axis=masa1y.pos-masa2y.pos, color= color.yellow, shaftwidth=0.005)
vm1x=arrow(pos=masa1x.pos, axis=vector(0,0,v1), shaftwidth=0.01) #wektory predkosci punktow
vm2x=arrow(pos=masa2x.pos, axis=vector(0,0,v2), color=color.green, shaftwidth=0.01)
vm1y=arrow(pos=masa1y.pos, axis=vector(0,0,v3), color=color.green, shaftwidth=0.01)
vm2y=arrow(pos=masa2y.pos, axis=vector(0,0,v4), color=color.green, shaftwidth=0.01)
#orbita1=ring(pos=vector(x1,0,0), axis=vector(1,0,0), radius=y1, thickness=0.01) #orbita
os=arrow(pos=vector(-2,0,0), axis=vector(4,0,0),color=vector(0.3,0.3,0.3),shaftwidth=0.005) #os obrotu
sila1=arrow(pos=masa1x.pos,axis=-vector(x1,y1,0)*Fdx, color= vector(1,1,0), shaftwidth=0.05) #wektory sil dosrodkowych punktow
sila2=arrow(pos=masa1x.pos,axis=-vector(-x1,-y1,0)*Fdx, color= vector(1,1,0), shaftwidth=0.05)
sila3=arrow(pos=masa1y.pos,axis=-vector(x2,y2,0)*Fdy, color= vector(1,1,0), shaftwidth=0.05)
sila4=arrow(pos=masa1y.pos,axis=-vector(-x2,-y2,0)*Fdy, color= vector(1,1,0), shaftwidth=0.05)
sumasilag=arrow(color= vector(0.8,0.5,0), shaftwidth=0.05) #suma sil dosrodkowych gora z Fd=mW^2ry
sumasilad=arrow(color= vector(0.8,0.5,0), shaftwidth=0.05) #suma sil dosrodkowych dol z Fd=mW^2ry
#sila1a=arrow(pos=masa1x.pos,axis=-vector(x1,y1,0)*Fdax, color= vector(1,1,0.5), shaftwidth=0.05) #wektory sil dosrodkowych punktow
#sila2a=arrow(pos=masa1x.pos,axis=-vector(x1,y1,0)*Fdax, color= vector(1,1,0.5), shaftwidth=0.05) #wektory sil dosrodkowych punktow
#sila3a=arrow(pos=masa1x.pos,axis=-vector(x1,y1,0)*Fday, color= vector(1,1,0.5), shaftwidth=0.05) #wektory sil dosrodkowych punktow
#sila4a=arrow(pos=masa1x.pos,axis=-vector(x1,y1,0)*Fday, color= vector(1,1,0.5), shaftwidth=0.05) #wektory sil dosrodkowych punktow
#sumasilga=arrow(color= vector(0.8,0.5,0), shaftwidth=0.05) #suma sil dosrodkowych dol F=am
#sumasilda=arrow(color= vector(0.8,0.5,0), shaftwidth=0.05) #suma sil dosrodkowych dol F=am
#sumaF=arrow(axis=-vector(0,Fd1+Fd2,0), color= vector(1,0.5,0), shaftwidth=0.03)
t=0
while t<20:
rate(3)
# print t,L
# print TIxx-TIxy-TIxz,-TIyx+TIyy-TIyz,-TIzx-TIzy+TIzz
# print TIxx,TIxy,TIxz," I ",TIyx,TIyy,TIyz," I ",TIzx,TIzy,TIzz
x1=x1-0.1 #nowe pozycje punktow
y1=sqrt(1-(x1*x1))
y2=y2-0.1
x2=-sqrt(1-(y2*y2))
v1=W.x*y1 # v = W x ry
v2=W.x*-y1
v3=W.x*y2
v4=W.x*-y2
ov1=1/v1 #1/v
ov2=1/v2
ov3=1/v3
ov4=1/v4
# print t,v1*ov1
r1=vector(x1,y1,0) #promienie
r2=vector(-x1,-y1,0)
r3=vector(x2,y2,0)
r4=vector(-x1,-y1,0)
# print mag(r1),mag(r2),mag(r3),mag(r4)
p1=mx*v1 #ped
p2=mx*v2
p3=my*v3
p4=my*v4
op1=1/p1 #1/p
op2=1/p2
op3=1/p3
op4=1/p4
# print "v",v1,v2,v3,v4, "p",p1,p2,p3,p4
wx=vector(y1*v1,-(x1*v1),0) # wx` = r x v12; r=1
wy=vector(y2*v3,-(x2*v3),0) # wy` = r x v34; r=1
Wk=wx+wy # omega koncowa Wk=wx`+wy`
# print t, "Ws=", W, "Wk=", Wk
a1=(v1*v1)/mag(r1) #przyspieszenia a=(v^2)/r; r=1
a2=(v2*v2)/mag(r2)
a3=(v3*v3)/mag(r3)
a4=(v4*v4)/mag(r4)
a1v=vector(x1,y1,0)*-a1 #wektory przyspieszen
a2v=vector(-x1,-y1,0)*-a2
a3v=vector(x2,y2,0)*-a3
a4v=vector(-x2,-y2,0)*-a4
# a1r=-r1*(v1*v1)
# f1am=a1*mx
# print t, f1am
# print t,a1,a2
if t<10: #suma par przyspieszen dosrodkowych gora, dol z Fd=mW^2ry
adg=a1v+a3v
add=a2v+a4v
else:
adg=a1v+a4v
add=a2v+a3v
Wax=vector(-ov1*a1v.y,ov1*a1v.x,0) # w = 1/v x a
Way=vector(-ov3*a3v.y,ov3*a3v.x,0)
Wa=Wax+Way #W=wx`+wy`
# print t, Wa
# r1=sqrt((x1*x1)+(y1*y1))
TIxx=(2*mx*((y1*y1)+(z1*z1)))+(2*my*((y2*y2)+(z2*z2))) #mx1 i mx2 --> 2*mx
TIyy=(2*mx*((x1*x1)+(z1*z1)))+(2*my*((x2*x2)+(z2*z2)))
TIzz=(2*mx*((x1*x1)+(y1*y1)))+(2*my*((x2*x2)+(y2*y2)))
TIxy=(2*mx*x1*y1)+(2*my*x2*y2)
TIxz=(2*mx*x1*z1)+(2*my*x2*z2)
TIyx=(2*mx*y1*x1)+(2*my*y2*x2)
TIyz=(2*mx*y1*z1)+(2*my*y2*z2)
TIzx=(2*mx*z1*x1)+(2*my*z2*x2)
TIzy=(2*mx*z1*y1)+(2*my*z2*y2)
L=vector((W.x*TIxx-W.y*TIxy-W.z*TIxz),(-W.x*TIyx+W.y*TIyy-W.z*TIyz),(-W.x*TIzx-W.y*TIzy+W.z*TIzz))
if y1<0: #wartosc sily dosrodkowe Fd=mW^2ry
Fdx=mx*W.x*W.x*y1
else:
Fdx=-mx*W.x*W.x*y1
if y2<0:
Fdy=my*W.x*W.x*y2
else:
Fdy=-my*W.x*W.x*y2
# print t, Fdy, x2,y2
Lpr1=vector(y1*p1,-x1*p1,0) # L = r x p
Lpr2=vector(-y1*p2,x1*p2,0)
Lpr3=vector(y2*p3,-x2*p3,0)
Lpr4=vector(-y2*p4,x2*p4,0)
Lprx=Lpr1+Lpr2
Lpry=Lpr3+Lpr4
Lpr=Lprx+Lpry #suma kretow
# print t, L-Lpr
Fd1=vector(x1,y1,0)*Fdx #wektory sil dosrodkowch z Fd=mW^2ry
Fd2=vector(-x1,-y1,0)*Fdx
Fd3=vector(x2,y2,0)*Fdy
Fd4=vector(-x2,-y2,0)*Fdy
if t<10: #suma par sil dosrodkowych gora, dol z Fd=mW^2ry
Fdg=Fd1+Fd3
Fdd=Fd2+Fd4
else:
Fdg=Fd1+Fd4
Fdd=Fd2+Fd3
Fd1a=a1v*mx #F=am
Fd2a=a2v*mx
Fd3a=a3v*my
Fd4a=a4v*my
WFpx=vector(-op1*Fd1a.y,op1*Fd1a.x,0) #w = (1/p) x F
WFpy=vector(-op3*Fd3a.y,op3*Fd3a.x,0)
WFp=WFpx+WFpy
# print t, WFp, W
if t<10: #suma par sil dosrodkowych gora, dol z F=ma
Fdag=Fd1a+Fd3a
Fdad=Fd2a+Fd4a
else:
Fdag=Fd1a+Fd4a
Fdad=Fd2a+Fd3a
print t,Fdag, Fdad
# kret.axis=vector(L.x,L.y,L.z+0.01)
kret2.axis=vector(Lpr.x,Lpr.y,Lpr.z+0.01)
# kret2x.axis=vector(Lprx.x,Lprx.y,Lprx.z+0.01)
# kret2y.axis=vector(Lpry.x,Lpry.y,Lpry.z+0.01)
masa1x.pos=vector(x1,y1,0)
masa2x.pos=vector(-x1,-y1,0)
masa1y.pos=vector(x2,y2,0)
masa2y.pos=vector(-x2,-y2,0)
promien1.pos=masa2x.pos
promien1.axis=masa1x.pos-masa2x.pos
promien2.pos=masa2y.pos
promien2.axis=masa1y.pos-masa2y.pos
vm1x.pos=masa1x.pos
vm1x.axis=vector(0,0,v1)
vm2x.pos=masa2x.pos
vm2x.axis=vector(0,0,v2)
vm1y.pos=masa1y.pos
vm1y.axis=vector(0,0,v3)
vm2y.pos=masa2y.pos
vm2y.axis=vector(0,0,v4)
# orbita1.pos=vector(x1,0,0)
# orbita1.radius=y1
# omegax.axis=wx
# omegay.axis=wy
# dv1.pos=vector(x1,y1,0)
# dv1.axis=vector(a1v.x,a1v.y,a1v.z)
# dv2.pos=vector(-x1,-y1,0)
# dv2.axis=vector(a2v.x,a2v.y,a2v.z)
# dv3.pos=vector(x2,y2,0)
# dv3.axis=vector(a3v.x,a3v.y,a3v.z)
# dv4.pos=vector(-x2,-y2,0)
# dv4.axis=vector(a4v.x,a4v.y,a4v.z)
# dvg.axis=vector(adg.x,adg.y,adg.z)
# dvd.axis=vector(add.x,add.y,add.z)
sila1.pos=vector(x1,y1,0)
# sila1.axis=vector(0,-mag(Fd1),0)
sila1.axis=vector(Fd1.x,Fd1.y,Fd1.z)
sila2.pos=vector(-x1,-y1,0)
# sila2.axis=vector(0,mag(Fd2),0)
sila2.axis=vector(Fd2.x,Fd2.y,Fd2.z)
sila3.pos=vector(x2,y2,0)
sila3.axis=vector(Fd3.x,Fd3.y,Fd3.z)
sila4.pos=vector(-x2,-y2,0)
sila4.axis=vector(Fd4.x,Fd4.y,Fd4.z)
# if t<10:
# sila3.axis=vector(0,-mag(Fd3),0)
# sila4.axis=vector(0,mag(Fd4),0)
# else:
# sila3.axis=vector(0,mag(Fd3),0)
# sila4.axis=vector(0,-mag(Fd4),0)
sumasilag.axis=vector(Fdg.x,Fdg.y,Fdg.z)
sumasilad.axis=vector(Fdd.x,Fdd.y,Fdd.z)
# sila1a.pos=vector(x1,y1,0)
# sila1a.axis=vector(Fd1a.x,Fd1a.y,Fd1a.z)
# sila2a.pos=vector(-x1,-y1,0)
# sila2a.axis=vector(Fd2a.x,Fd2a.y,Fd2a.z)
# sila3a.pos=vector(x2,y2,0)
# sila3a.axis=vector(Fd3a.x,Fd3a.y,Fd3a.z)
# sila4a.pos=vector(-x2,-y2,0)
# sila4a.axis=vector(Fd4a.x,Fd4a.y,Fd4a.z)
# sumasilga.axis=vector(Fdag.x,Fdag.y,Fdag.z)
# sumasilda.axis=vector(Fdad.x,Fdad.y,Fdad.z)
# sumaF.axis=sila1.axis+sila2.axis
# LxF=sumaF.axis.x*L.x+sumaF.axis.y*L.y+sumaF.axis.z*L.z
# print t,"L x F",LxF
t=t+1
Inne tematy w dziale Technologie

