W wątku Elektrodynamika dla bardzo opornych zadałem blogerowi SYZYF pytanie:
Funkcja tangens jest ciągła?
a on odpowiedział (05.06.2012 23:21):
Nadanie innej nazwy liczbom naturalnym nic tu nie zmieni...
Ta odpowiedź wskazuje, że funkcja tangens jest albo ciągła albo nieciągła.
W tych okolicznościach zaglądam do Wikipedii i czytam:
Funkcja rzeczywista zmiennej rzeczywistej (określona na całym zbiorze  lub jego podprzedziale, skończonym lub nie) może być postrzegana jako ciągła, jeżeli jej wykres można „narysować bez odrywania ołówka od papieru” (bez ograniczeń w czasie lub przestrzeni).
lub jego podprzedziale, skończonym lub nie) może być postrzegana jako ciągła, jeżeli jej wykres można „narysować bez odrywania ołówka od papieru” (bez ograniczeń w czasie lub przestrzeni).
Nie potrafię narysować wykresu funkcji tangens na niezawiniętej płaszczyźnie Euklidesa "bez odrywania ołówka od papieru"

bo tangensoida ma jeden koniec na dole, a drugi u góry i to ładnie widać w pobliżu takich punktów jak 90° (π/2) , a więc funkcja tangens jest nieciągła.
Wchodzę dalej do Wikipedii i czytam dalej:
"Wartość bezwzględna a. moduł – dla danej liczby rzeczywistej wartość liczbowa nieuwzględniająca znaku liczby."
Tangensoida w wartościach bezwzględnych także będzie nieciągła, bo dla takich kątów jak 90° (π/2), jest po prostu nieokreślona:
| radiany |
 |
 |
 |
 |
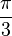 |
 |
 |
| stopnie |
 |
 |
 |
 |
 |
 |
 |
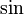 |
 |
 |
 |
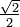 |
 |
 |
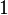 |
 |
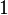 |
 |
 |
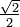 |
 |
 |
 |
 |
 |
 |
 |
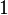 |
 |
 |
nieokreślony |
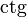 |
nieokreślony |
 |
 |
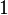 |
 |
 |
 |
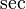 |
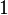 |
 |
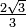 |
 |
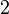 |
 |
nieokreślony |
 |
nieokreślony |
 |
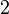 |
 |
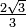 |
 |
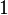 |
http://pl.wikipedia.org/wiki/Funkcje_trygonometryczne
a liczby nieokreślonej takiej jak tg(pi/2) = sin(pi/2)/cos(pi/2) = 1/0 nie rysuje się, bo takie liczby są nieznane i nie wiadomo, czy są elementami zbioru 
Z braków odpowiedzi jakie dostaję od rozmówców wyłania się taki obraz współczesnych poglądów na ten temat:
Funkcja tangens tg(x) dla x dążących do pi/2 dąży do nieskończoności →∞ lecz nie wiadomo czy ją osiąga i nie wiadomo jaką ma wartość w punkcie x=pi/2 bo taka liczba 1/0 nie jest znana.
Nie wiadomo także, czy funkcja tamgens jest nieokreślona tylko dla samego punktu x=pi/2 czy również dla otoczenia tego punktu, a więc punktów położonych bardzo blisko pi/2.
pytanie:
Czy powyższa Wielka Tajemnica Wiary Matematycznej jest TABU i czy wolno rozwiązać tę zagadkę?
 mędrzec Edward Robak* z Nowej Huty
mędrzec Edward Robak* z Nowej Huty 
image fo posta: 7.06.2012 18:23

image fo posta: 12.06.2012 12:12

Inne tematy w dziale Technologie

