nieznana tajemnica grawitacji

Jak się nie przewrócisz, to się nie nauczysz - mawiają górale, ucząc ceprów jazdy na nartach. Człowiek się przewraca, bo "Ziemia go przyciąga". To przyciąganie ma nazwę SIŁA i zależy od ilości masy przyciąganej. Można zmierzyć tę siłę za pomocą WAGI. Dawniej jednostką siły był 1 kG = kiliogram-siła.

Przyciąganie ziemskie jest przejawem prawa odkrytego i sformalizowanego przez Isaaca Newtona (1643-1727), prawa o nazwie... (?) MOŻNA PROSIĆ PODPOWIEDŹ?

Użył łacińskiego słowa gravitas (ciężar) do nazwania siły, którą obecnie znamy pod nazwą grawitacji i zdefiniował prawo powszechnego ciążenia.

Acha prawo powszechnego ciążenia

Między dowolną parą ciał posiadających masy pojawia się siła przyciągająca, która działa na linii łączącej ich środki, a jej wartość rośnie z iloczynem ich mas i maleje z kwadratem odległości.

W powyższej definicji użyto słowa: pojawia się a to słowo kłuje w oczy. W angielskiej Wikipedii jest tak:

Every point mass attracts every single other point mass by a force pointing along the line intersecting both points. The force is proportional to the product of the two masses and inversely proportional to the square of the distance between them

w tłumaczeniu Google:

Każda masa punktowa przyciąga (attracts) każdą inną masę punktową z siłą skierowaną wzdłuż linii przecięcinającej oba punkty. Siła jest proporcjonalna do iloczynu dwóch mas i odwrotnie proporcjonalna do kwadratu odległości między nimi.

Nie ma więc w oryginale pojawiania się , lecz jest przyciąganie się. Ta siła JEST zawsze, nie może więc pojawiać się (i znikać) - bo ta siła JEST a-czasowa.

Siła przyciągania pomiędzy dwoma punktami fizycznymi o niezerowej masie bezwładnej - nie zależy od UPŁYWU CZASU, lecz od objętości grawitacyjnej, która to objętość jest niezmiennikiem.

V_G = F∙ r² = G∙m₁∙m₂ =const

Można wyliczyć jednostkę objętości grawitacyjnej:

[kg∙m/s²] ∙ [m²] = [m³ / kg∙s²] ∙ [kg²] = kg ∙ m³ / s²

kg - masa bezwładna, m³ - objętość geometryczna, 1/ s² - częstotliwość kwadratowa

interpretacja:

Objętość grawitacyjna V_G rózni się od objętości geometrycznej V tym, że objętość geometryczna V m³ jest pusta, natomiast objętość grawitacyjna V_G zawiera masę kg i parametr 1/ s² będący częstotliwością kwadratową.

Herc (Hz) – jednostka miary częstotliwości w układzie SI (jednostka pochodna układu SI) i w wielu innych, np. CGS, MKS i MKSA. Definiuje się ją jako liczbę cykli na sekundę.

1 Hz = 1 / (1 s) = 1 s^-1

Nazwa jednostki pochodzi od nazwiska niemieckiego fizyka Heinricha Hertza, zajmującego się m.in. badaniem fal elektromagnetycznych.

Zachodzi podobieństwo pomiędzy częstotliwością kwadratową i różniczką częstotliwości:

(1/s)² = 1/s² podnoszenie do kwadratu

(1∙s^-1)' = -1∙s^-2 = - 1/s²różniczkowanie wg: (xⁿ)’ = n∙x^n-1

Kwadrat częstotliwości od różniczki częstotliwości różni się tylko znakiem. Różniczka jest ujemna.

Na grafach, grafikach, rysunkach, animacjach przedstawia się siłę przyciągania F jako dwie siły F₁ i F₂, ale to nie są dwie siły lecz JEDNA, która podobnie jak kij, ma zawsze dwa końce. F₁ i F₂ to dwa końce jednej siły F.

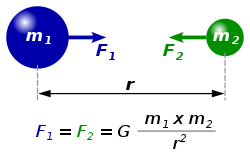
Mechanizmy prawa powszechnego ciążenia Newtona; masa punktu m₁ przyciąga masę innego punktu m₂ z siłą F₂, która jest proporcjonalna do iloczynu obu mas i odwrotnie proporcjonalna do kwadratu odległości (r) między nimi. Niezależnie od masy lub odległości, wielkość |F₁| i |F₂| będzie zawsze równa. G jest stałą grawitacyjną

Jest więc prawo powszechnego ciążenia prawem powszechnego przyciągania.

Siła przyciągająca przypomina naciągniętą sprężynę, która jednym końcem przyciąga jedno ciało, a drugim końcem przyciąga drugie ciało, tak jak ta biała spręzyna grawitacji z poprzedniej notki pt: bardzo ciekawa własność grawitacji

Prawo powszechnego ciążenia, czyli PRAWO POWSZECHNEGO PRZYCIĄGANIA - bardzo dobrze działa tam gdzie działa, natomiast tam gdzie nie działa mówi się o anomaliach (np anomalia flyby ), wymyśla się ciemną materię, a w mechanice kwantowej ignoruje się Newtona np. poprzez zasadę nieoznaczoności i jej nadinterpretacje.

historia: Robert Hooke zarzucił Newtonowi plagiat w kwestii prawa odwrotnych kwadratów, a więc o to, że końce siły F przyłożone są w środkach ciężkości przyciągających się ciał.

A jak to wynika z rachunku? Czy rzeczywiście środek ciężkości ciała (punkt wokół którego masa się kręci) jest równoważny z punktem przyłożenia siły?

Można to sprawdzić. Na początek dla ciała m₁, które jest sześcianem o jednakowej gęstości (kryształ). W idealizacji wygląda to tak.

Punkt sześcienny m₁ o boku a znajduje się w odległości r od punktu m₂ .

Siła pomiędzy tymi punktami F = G∙m₁∙m₂ / r²

A co się stanie, gdy ten sześcienny punkt przedzielimy na dwie połowy?

Ano stanie się to, że każda z połówek będzie miała swoją siłę z punktem m₂

F = V_G / r²

F_a = V_G / (2∙( r + a/4)²)

F_b = V_G / (2∙( r - a/4)²)

Te siły powinny się sumować, a więc F ma być równe F_a + F_b, bo punkt sześcienny JEST ten sam. Zmienił się tylko sposób obliczenia. Ale czy są równe?

Dla V_G = 1, a = 4, r = 100

F = 1 / 100²

F_a = 1 / (2∙101²)

F_b = 1 / (2∙99²)

F_a + F_b = 1 / (2∙ 101²) + 1 / (2∙99²) =/= 1 / 100²