Prezentacja prawa znikomego działania

Wstęp

 Prawo znikomego działania obecnie w fizyce nie jest znane. Z tego powodu nie jest ono stosowane w interpretacji wielu fizycznych zjawisk. Prawo znikomego działania przejawia się w kilku fizycznych zjawiskach. Wśród nich jest przenikanie kulistego pioruna przez okienną szybę, które inicjuje sama przyroda, oraz przejawianie się tego prawa w efekcie Boreal, który został odkryty przez prof. Louisa Rancourta, fizyka z College Boreal, w Kanadzie.*1) Ale w najbardziej efektowny sposób prawo znikomego działania prezentuje się w akceleratorach cząstek. Tam badacze fizyki cząstek rozpędzają cząstki do ogromnych prędkości i w naturalny sposób stykają się z prawem znikomego działania. Jednak obecnie fizycy obserwowane tam zjawiska interpretują w niewłaściwy sposób. Dla zrozumienia przez fizyków oraz przez wszystkich innych ludzi, czym jest prawo znikomego działania, będzie tutaj przedstawiona komputerowa wersja prezentacji prawa znikomego działania. 

Założenia do modelowania prawa znikomego działania

Do modelowania prawa znikomego działania były wykorzystane komputerowe programy: Gas2n_A.exe i pliki z rozszerzeniem .gas oraz AtomStand.exe i pliki z rozszerzeniem .ato. Do modelowania posłużyły dwie cząstki oznaczone numerami 1 i 2. Na początku cząstki 1 i 2 znajdują się względem siebie nieruchomo w pewnych położeniach. Następnie cząstka 1 zaczyna poruszać się z określoną prędkością wzdłuż osi X obok cząstki 2. Ten ruch oraz wzajemne oddziaływanie cząstek 1 i 2 przyczynia się do powstania ruchu obu cząstek wzdłuż osi Z. Wzdłuż tej osi Z cząstki poruszają się z jednakową prędkością, ale w przeciwnych kierunkach. Wielkość tej prędkości cząstek 1 i 2 wzdłuż osi Z zmienia się w zależności od początkowej prędkości cząstki 1. I właśnie zmiany prędkości cząstek 1 i 2 wzdłuż osi Z, w zależności od początkowej prędkości cząstki 1, są modelowym świadectwem przejawiania się prawa znikomego działania w zjawiskach fizycznych. 

Funkcje oddziaływania cząstek materii

Wzajemne przyspieszanie się cząstek materii ma złożoną postać. Można w nim wyróżnić składową grawitacyjną i składową strukturalną.

Grawitacyjne przyspieszenie badał Newton i wyniki swoich badań przedstawił w postaci matematycznej formuły.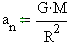

Dzisiaj wiadomo, że grawitacyjne oddziaływanie nie zmienia się dokładnie tak, jak to przedstawił Newton. Bo jeśli ono przy zmianie odległości zmieniałoby się dokładnie według prawa Newtona, to wówczas orbity planet w Układzie Słonecznym miałyby dokładny kształt elipsy. A takiego kształtu nie mają. Najbardziej wyrazistym przykładem jest zjawisko, które jest znane jako ruch peryhelium Merkurego.*2) Ruch peryhelium Merkurego jest powolny - jego wielkość jest równa 42,98 kątowych sekund na stulecie. Ale istnienie tego ruchu świadczy o tym, że faktyczna orbita tej planety ma kształt rozety. Zmienność orbity Merkurego można opisać bardziej dokładnie, jeśli w funkcji Newtona dopisać eksponencjalny czynnik. Wówczas zmienność grawitacyjnego przyśpieszenia można zapisać za pomocą funkcji w postaci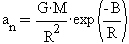. Przy analizie ruchu lepiej jest korzystać z tej funkcji, ale zapisanej jako natężenie pola, które zmienia się w zależności od odległości R. Można ją także zapisać dopisując znak "minus", który jest tutaj rekomendowany po to, aby funkcja potencjalnego pola była dodatnia. Wówczas funkcja natężenia pola wzdłuż dowolnego promienia, który wychodzi z centralnego punktu pola, ma postać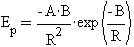, a potencjał takiego pola jest opisywany przez eksponencjalną funkcję, czyli przez funkcję E w postaci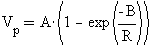. W tych wzorach A jest współczynnikiem proporcjonalności, a B jest eksponencjalnym współczynnikiem.

Przy dużych odległościach R (w skali kosmosu) zapisane w ten sposób parametry pola grawitacyjnego ciała niebieskiego i parametry według zapisu, który przedstawił Newton, różnią się od siebie w małym stopniu. Dlatego że przy wzroście odległości eksponencjalny czynnik exp(-B/R) dąży do jedynki. Ale eksponencjalny czynnik odgrywa dużą rolę przy opisie pól pojedynczych składników materii, takich jak fundamentalne cząstki, atomy, molekuły, a także przy opisie ich wzajemnych przyśpieszeń przy małych odległościach, rzędu odległości między składnikami w jądrze atomu i odległości między atomami. 

Wykresy tych funkcji są przedstawione poniżej. 

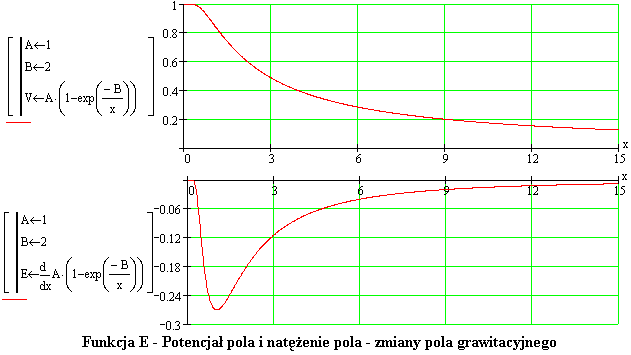
A na poniżej przedstawionych wykresach funkcji widać, że przy kosmicznych odległościach różnica oddziaływania grawitacyjnego wg wzoru Newtona i według eksponencjalnej funkcji E, czyli tego samego wzoru, ale z eksponencjalnym czynnikiem, jest niezauważalna. 

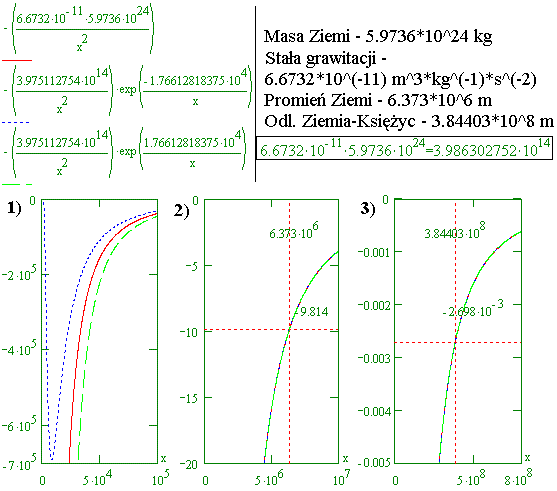
Z obliczeń wynika, że w odległości, w jakiej Księżyc znajduje się od Ziemi, przyspieszenie ziemskie wg Newtona wynosi ok. 0,002690146399 m/s^2. Natomiast gdy do wzoru Newtona dopisać eksponencjalny czynnik, wówczas wg tego eksponencjalnego wzoru przyspieszenie ziemskie w miejscu położenia Księżyca wynosi ok. 0,002690270004 m/s^2. Różnica wynosi 123,605*10^9 m/s^2 i świadczy ona o istnieniu ruchu peryhelium Księżyca. Oczywiście, świadczy także o istnieniu ruchu peryhelium Ziemi oraz o orbitach Ziemi i Księżyca w postaci rozety, a nie elipsy. 

Komputerowe modelowanie prawa znikomego działania

W komputerowym modelowaniu ruchu cząstek 1 i 2 względem siebie można wpierw wykorzystać grawitacyjną składową oddziaływania między cząstkami. Uzyskane wyniki są przedstawione poniżej w postaci kropkowego wykresu 1) E. 

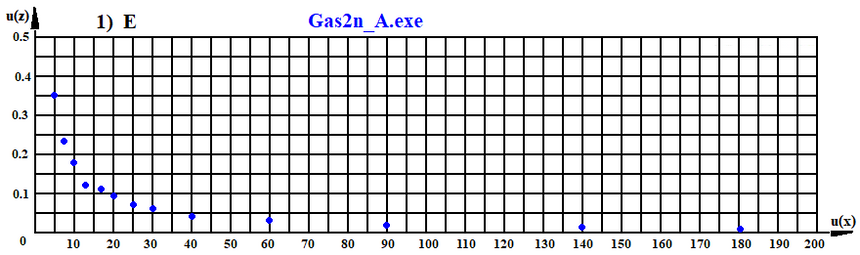
Wyniki oddziaływania przy prędkości cząstki 1 mniejszej niż 5 jednostek prędkości nie są przedstawiane, bo wówczas cząstki 1 i 2 poruszają się jako jedna całość, czyli jako stabilna struktura.

Dla jasności trzeba tu dodać, że podczas przeprowadzania tych ćwiczeń w programie Gas2n_A.gas w tablicy "Formula" aktywna była funkcja E. 

W kolejnych ćwiczeniach wykorzystano właściwości strukturalnej składowej oddziaływania między cząstkami, a konkretnie, właściwości potencjałowych (potencjalnych) powłok. W ćwiczeniach były wykorzystane dwie cząstki (z numerami 1 i 2) i każda z nich miała jedną potencjałową powłokę o promieniu 2 jednostki długości. Dwie identyczne cząstki, gdy są oddalone od siebie na odległość 2,1 j.dl., to wówczas każda z nich znajduje się w obszarze potencjałowej powłoki swojej sąsiadki. Pozostawione w spokoju tworzą stabilną strukturę, ale pozostają w nieustannym ruchu względem siebie.

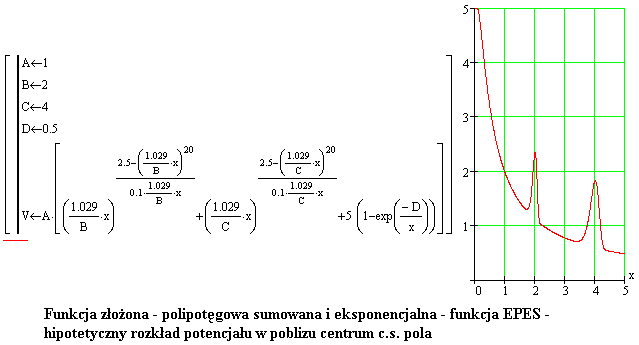
Poniżej jest przedstawiony rysunek z wykresami potencjału pola oraz natężenia pola cząstki z dwoma potencjałowymi powłokami. Powłoki mają promienie 2 i 4 j.dl. 

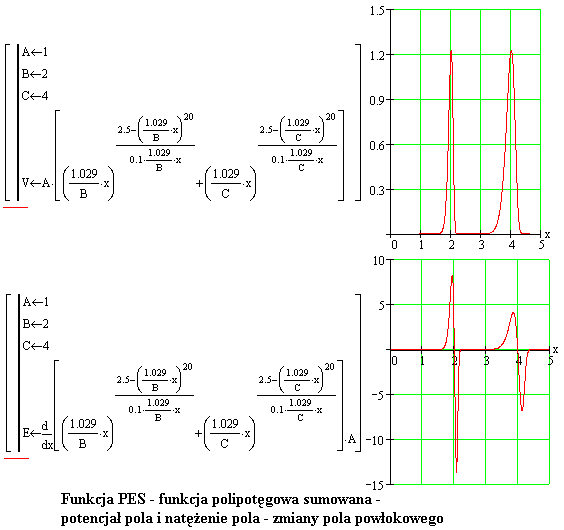
W tych odległościach od centrum cząstki znajdują się punkty z ekstremalnym potencjałem powłoki. Znajdująca się w obszarze powłoki druga podobna cząstka drga niejako między zboczami tej potencjałowej powłoki. Oczywiście, drgają obie cząstki względem siebie. Bo są to jednakowe cząstki i każda z nich znajduje się w obszarze potencjałowej powłoki swojej sąsiadki.

Przed przeprowadzeniem ćwiczeń z dwoma cząstkami, drgającymi na powłokach sąsiadki, ich ruch został wyhamowany niemal do zera. Do wyhamowania ruchu cząstek w programie Gas2n_A.exe posłużył przycisk "Cool". Po wyhamowaniu drgającego ruchu cząstki znajdowały się na osi Z w jednakowej odległości od punktu 0. Przed rozpoczęciem dalszych ćwiczeń cząstka 1 została przesunięta równolegle do osi X "w lewo" - rzędna pozostała bez zmiany, a odcięta była równa -5. Z tego położenia rozpoczynał się ruch cząstki 1 "w prawo"; w kolejnych ćwiczeniach z coraz to inną prędkością.

Wyniki modelowania ruchu cząstek 1 i 2 względem siebie przy wykorzystaniu strukturalnej składowej oddziaływania cząstek są przedstawione poniżej w postaci kropkowego wykresu 2) PES. 

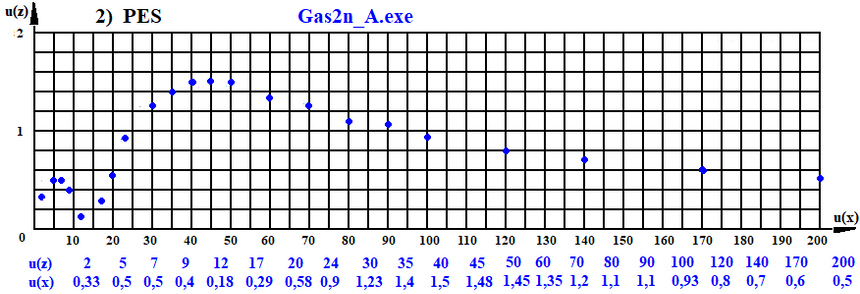
W tym przypadku przy prędkości poniżej 12 j. pr. widoczne jest pewnego rodzaju zaburzenie. To zaburzenie jest wynikiem dłuższego czasu oddziaływania ze sobą cząstek 1 i 2, czyli jest wynikiem stosunkowo małej prędkości cząstki 1. W tym czasie cząstki znajdują się w obszarze potencjałowej powłoki swojej sąsiadki i drgają względem siebie. W wyniku tego drgania końcowy wynik ich prędkości wzdłuż osi Z zmienia znak z minusa na plus lub odwrotnie. 

W obu wersjach ćwiczeń z dwoma cząstkami, czyli przy wzajemnym oddziaływaniu cząstek zgodnie z grawitacyjną funkcją E, jak i zgodnie ze strukturalną funkcją PES, przejawia się prawo znikomego działania. Istota tego prawa jest bardzo prosta - zwiększanie (w kolejnych ćwiczeniach) prędkości cząstki 1 przyczynia się do zmniejszania wzajemnego oddziaływania ze sobą cząstek 1 i 2. Ale istnieje znacząca różnica. W przypadku oddziaływania cząstek zgodnie z funkcją PES prawo znikomego działania zaczyna przejawiać się dopiero wówczas, gdy prędkość cząstek względem siebie przekracza pewną wielkość. Ale dla znaczenia prawa znikomego działania w przyrodzie ta różnica nie jest istotna. Bo oba te rodzaje oddziaływania są ze sobą nierozłącznie związane i są zakodowane w budowie cząstek materii.

Poniżej są przedstawione schematyczne wykresy matematycznych funkcji, które są związane z tymi oddziaływaniami i je opisują. 

Potencjałowe powłoki cząstek materii są podstawą budowy wszelkiego rodzaju struktur w przyrodzie. Dzięki jądrowym potencjałowym powłokom protonów i neutronów, które w najbliższej odległości otaczają centrum każdego nukleonu, powstają atomy wszystkich pierwiastków chemicznych. Dzięki molekularnym potencjałowym powłokom, które otaczają centrum każdego nukleonu i mają znacznie większe promienie niż powłoki jądrowe, powstają molekuły wszystkich związków chemicznych oraz wszelkiego rodzaju trwałe struktury materii. Dzięki oddziaływaniu potencjałowych powłok istnieje wytrzymałość materii na rozrywanie i ściskanie, sprężystość. W materii istnieją wszelkiego rodzaju opory dla rozprzestrzeniania się różnego rodzaju fal, cząstek i większych obiektów.

Właśnie te opory, w ich elementarnej postaci, są widoczne na poniższym kropkowym wykresie 3) EPES. 

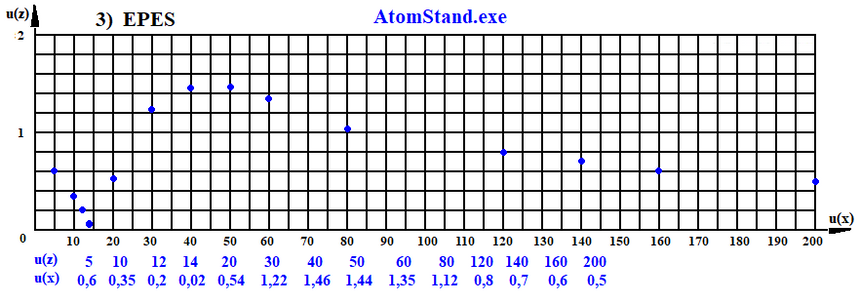
Na wykresie te opory występują (w przybliżeniu), gdy prędkość cząstki 1 wynosi od 14 j.pr. do 45 j.pr. Przy takiej prędkości ruchu cząstki 1 wzrost jej prędkości wzdłuż osi X powoduje wzrost prędkości cząstek 1 i 2 wzdłuż osi Z. Przy prędkościach cząstki 1 większych od 45 j.pr. (w przybliżeniu) występuje zmniejszanie się wzajemnego oddziaływania cząstki 1 z cząstką 2. Wyraża się to w postaci ich malejących prędkości wzdłuż osi Z. Inaczej mówiąc, zmniejszają się opory, jakie stawia cząstka 2 dla ruchu cząstki 1. 

Funkcjonowanie prawa znikomego działania

Przedstawiane tu prawo znikomego działania funkcjonuje w dwóch rodzajach zjawisk.

Jeden rodzaj zjawisk jest związany z cząstkami, które z ogromną prędkością poruszają się liniowo względem jakiegoś obiektu. Pędząca z ogromną prędkością jedna cząstka oraz cząstki materii, względem których ona się porusza, wpływają na siebie w znikomym stopniu. Taka sytuacja istnieje w dwóch znanych zjawiskach. Jednym z nich jest ruch cząstek rozpędzonych do ogromnych prędkości w akceleratorze cząstek. Tam cząstki poruszają się w próżni, ale pokonują one hamujący wpływ otaczającej materii samego akceleratora oraz materii fizycznej próżni, która nie jest próżnią absolutną.

Innym przykładem liniowego ruchu jest neutrino. Neutrina docierają do nas z ogromną prędkością z kosmosu, ale także zostają wyrzucane w przestrzeń podczas rozpadu atomów promieniotwórczych pierwiastków w obszarze Ziemi. Dzięki swojej ogromnej prędkości zgodnie z prawem znikomego działania przenikają głęboko do wnętrza Ziemi. 

Parametry cząstek, które w akceleratorach są przyspieszane do dużych prędkości, są obecnie przez fizyków teoretyków błędnie interpretowane. Ma to związek z niewłaściwym rozumieniem i interpretowaniem takich pojęć, jak energia i masa. Od prawie stu dwudziestu lat w fizyce jest stosowana błędna formuła E=m*c^2. Opierając się na niej obecnie fizycy teoretycy błędnie uważają, że zużywana energia w akceleratorach na przyspieszanie cząstek zamienia się w masę tych cząstek. Uważają oni, że właśnie to jest przyczyną coraz większych trudności w procesie przyspieszania cząstek, które poruszają się z coraz większą prędkością. A rzeczywisty stan rzeczy jest taki, że kiedy w akceleratorach coraz trudniej przyspieszać cząstkę, gdy ma ona coraz większą prędkość, to jest to wynikiem coraz mniejszych możliwości wpływania akceleratora na cząstkę. 

Drugi rodzaj zjawisk, w których przejawia się prawo znikomego działania, jest związany z drgającym ruchem cząstek materii.

Odkrycia w tej dziedzinie dokonał prof. Louis Rancourt, fizyk z College Boreal, w Kanadzie. Swoje odkrycie nazwał on efektem Boreal.

W jednym ze swoich eksperymentów prof. Rancourt wykorzystywał dwie masy - 100 g i 500 g. Mniejszą masę umieszczał na wadze skrętnej, a większą masę umieszczał nieopodal mniejszej masy. Po ustabilizowaniu położenia (zamocowanej na wadze) mniejszej masy względem większej masy badacz przepuszczał przez przestrzeń między obu masami wiązkę laserowego światła (w innym doświadczeniu była to wiązka zwykłego światła). Skutek był taki, że mniejsza masa przybliżała się do większej. 

W innym doświadczeniu badacz nie korzystał z oddziaływania większej masy na mniejszą, a miał jedynie wagę skrętną i zawieszony na niej ciężarek o masie 100 g. W tym doświadczeniu przepuszczał on wiązkę światła przez przestrzeń niedaleko od ciężarka, na przykład, od północnej strony. Ciężarek pod wpływem oddziaływania wiązki światła przesuwał się na północ, czyli przybliżał się do wiązki światła. A kiedy światło przepuszczał nieopodal ciężarka od strony południowej, to wówczas ciężarek odchylał się na południe. 

Doświadczenia były przeprowadzane w różnych warunkach, w tym także i w piwnicy. W każdym przypadku w różnych miejscach piwnicy, bądź w różnych miejscach laboratorium, ramię wagi skrętnej z zawieszoną masą ustawiało się w różnych kierunkach. O kierunku decydowało miejsce położenia najbliższych dużych mas materii - muru, oprzyrządowania itd. I w każdym doświadczeniu było tak, że wraz z załączeniem promienia światła zawieszona na ramieniu wagi skrętnej masa zbliżała się do promienia światła, a gdy tylko promień świetlny wyłączono, następował powrót ramienia z masą do pierwotnego położenia. 

Dla wyjaśnienia efektu Boreal nie jest polecana interpretacja, jaką proponuje odkrywca. Bo nawet jeśli dla wyjaśnienia fizycznego mechanizmu efektu Boreal korzystać z pojęcia różnicy ciśnień, to wcale nie oznacza, że ten mechanizm jest związany akurat z oddziaływaniem grawitacyjnym. Bo w istocie dzisiejsza teoretyczna fizyka nie zna mechanizmu działania grawitacji. Obecnie ten mechanizm - samej grawitacji, a także efektu Boreal - można logicznie wyjaśnić jedynie na podstawie idei, które są zawarte w konstruktywnej teorii pola (KTP).*3)

Więcej na temat efektu Boreal można przeczytać artykule "Efekt Boreal - Prawo znikomego działania".*1) 

W rzeczywistości, w efekcie Boreal przejawia się prawo znikomego działania, które jest związane z drgającym ruchem cząstek materii. Cząstki materii przenoszą promieniowanie świetlne. Drgając z dużą częstotliwością, poruszają się z dużą prędkością. Wskutek tego w znacznym stopniu zmniejszają wzajemne oddziaływanie z cząstkami materii z otoczenia. Dzięki temu zostaje zniszczona równowaga w oddziaływaniach między cząstkami materii. A kiedy po pojawieniu się promienia świetlnego, znajdujący się niedaleko obiekt zaczyna poruszać się, to jest to w pewnym sensie dążenie składników materii do utworzenia stanu równowagi w nowo powstałej sytuacji. 

Efekt Boreal świadczy o tym, że próżnia, czyli pozbawiona atomów przestrzeń, jest wypełniona cząstkami subtelnej materii. W tej próżni fale świetlne rozchodzą się w podobny sposób, jak fale dźwiękowe rozchodzą się np. w powietrzu. Cząstki subtelnej materii, których istnienie potwierdzają wyniki fizycznych doświadczeń prof. Louisa Rancourta, w konstruktywnej teorii pola (KTP) zostały nazwane protoelektronami. 

Zakończenie

Przedstawiona tutaj prezentacja prawa znikomego działania jest skierowanym do fizyków teoretyków wezwaniem. To wezwanie ma na celu pobudzenie fizyków teoretyków do działania w kierunku naprawy teoretycznej fizyki.

___________________________________

*1) Opis zjawiska znajduje się w artykule "Efekt Boreal - Prawo znikomego działania" na http://pinopa.narod.ru/12_C3_Effect_Boreal_pl.pdf.

*2) Istota zjawiska jest przedstawiona w artykule "Ruch peryhelium Merkurego" na http://pinopa.narod.ru/14_C3_Ruch_peryhelium.pdf.

*3) "Konstruktywna teoria pola - krótko i krok po kroku" - http://pinopa.narod.ru/KTP_pl.pdf.

Bogdan Szenkaryk "Pinopa"

Polska, Legnica, 2024.02.23.