motto:
this model of vertical accleration fits Miller data (Zal.2) as well as MAK report data, with noisy wave-like behavior omitted
you-know-who
Jak niektórym zapewne wiadomo, postanowiłem nałożyć rys.8, zaprezentowany w opracowaniu you-know-who , na mapkę satelitarną przez zaczepienie rys.8 w pancernej brzozie. Efekt, w całej okazałości i w dużej rozdzielczości, można obejrzeć na mojej galerii na picasie (LINK). Opisałem tam również moje zastrzeżenia do trajektorii wyliczonej przez you-know-who, co zaraportowałem także na jego blogu. Niestety, you-know-who nie przejął się tym zbytnio i dalej pewnie twierdzi, że jego model jest zgodny z zarejestrowanymi ścięciami drzew. OK, można i tak, jednak to nie koniec problemów.
By było wiadomo o co chodzi w dalszej części - poglądowy rysunek:

Łatwo zauważyć, że koniec lewego statecznika (jego tor to przerywana linia niebieska), który miał wykonać ścięcie topoli przy ulicy Kutuzowa, przechodzi w tym obszarze w odległości około 8 metrów od toru środka masy (czarna linia) a kąt obrotu samolotu wynosi 120-130 stopni. Obliczmy to więc:

|
obrót [stopnie]
|
10
|
20
|
30
|
40
|
50
|
60
|
70
|
80
|
90
|
100
|
110
|
120
|
130
|
140
|
150
|
|
odl.statecznik (a) [m]
|
7,89
|
8,9
|
9,63
|
10,07
|
10,2
|
10,02
|
9,54
|
8,77
|
7,73
|
6,46
|
4,99
|
3,37
|
1,65
|
-0,12
|
-1,89
|
|
odl.skrzydło (b) [m]
|
12,95
|
12,22
|
11,13
|
9,7
|
7,97
|
6
|
3,84
|
1,57
|
-0,74
|
-3,04
|
-5,24
|
-7,28
|
-9,1
|
-10,65
|
-11,87
|
Z powyższej tabelki wynika, że przy obrocie o 120-130 stopni, odległość końca lewego statecznika od środka masy powinna wynosić 3,4 - 1,7m, skąd więc 8 metrów u you-know-who?
By znaleźć odpowiedź na to pytanie trzeba zagłębić się w program ykw101-26x.pro. Winny jest ten fragment (linie 291- 309):
291: ; 18 m is the distance between the wing and tail
292: delt=18./(vv+wind_x) ; time delay between wings and tail passing an object
293: ; the tail is banked more at a given ground object
294: pt = pp +ww/180*!pi*delt +dw/180*!pi*delt^2/2. ; tail bank angle
295: deltw= -16./(75+wind_x) ; time delay between front wheel and C.M. < 0
296: pw = pp +ww/180*!pi*deltw +dw/180*!pi*deltw^2/2. ; front wheel bank
297: y_L_tail = 6.7*cos(pt)+7.6*sin(pt)
298: z_L_tail = -6.7*sin(pt)+7.6*cos(pt) -18*sin(pitch)
299: z_fw = -5*cos(pw) +15*sin(shift(pitch,-1000*deltw))
300: ztrack_fw = track_z_cm + z_fw
301: ztrack_fw = ztrack_fw(-1000*deltw:*)
302:
303: track_cm = yy +(72.-13.5) ; 72m is the rwy-birch, and ~13 the c.m.-birch dist.
304: ;the MAK centerline seems to disagree with the direction to NDB by ~10m laterally
305:
306:
307: xtrack_L_tail = xx -18. ; 18m is the impact-point-on-wing to tail distance
308: ytrack_L_tail = track_cm + y_L_tail
309: ztrack_L_tail = track_z_cm + z_L_tail
Tylko kilkanaście linii kodu, a dwa błędy! Zaznaczyłem je na czerwono.
1. "293: the tail is banked more at a given ground object"- niewątpliwie prawda, z tym, że jednocześnie współrzędna x brana do określenia trajektorii końca lewego skrzydła xtrack_L_tail jest przesunięta o -18 m (linia 307), czyli jednak należy wziąć kąt pp. Prawidłowo:
297: y_L_tail = 6.7*cos(pp)+7.6*sin(pp)
2.Samo obliczenie odległości końca lewego skrzydła od środka masy, zrzutowanej na oś OY, jest poprawne (z uwzględnieniem uwagi z p.1) , wzór:
297: y_L_tail = 6.7*cos(pt)+7.6*sin(pt)
jest równoważny stosowanemu powyżej przeze mnie. Jednak obliczenie przesunięcia jest błędne. Linie:
307: xtrack_L_tail = xx -18. ; 18m is the impact-point-on-wing to tail distance
308: ytrack_L_tail = track_cm + y_L_tail
oznaczają, że oś samolotu jest cały czas równoległa do osi OX. Tymczasem, w pierwszym przybliżeniu, można przyjąć, iż jest ona styczna do trajektorii środka masy. Co ciekawe, you-know-who stosuję tą zasadę dla obliczenia toru końca kikuta lewego skrzydła (na przykład linia 284), tu jednak zapomniał. Wobec powyższego:
307: xtrack_L_tail = xx -18.*cos(kk/180.*!pi)-y_L_tail*sin(kk/180.*!pi) ; 18m is the impact-point-on-wing to tail distance
308: ytrack_L_tail = track_cm - 18.*sin(kk/180.*!pi) +y_L_tail*cos(kk/180.*!pi)
Zachęcony tak łatwym "sukcesem" postanowiłem sprawdzić cały program you-know-who, chociaż IDL nie jest dla mnie językiem pierwszego wyboru ;) I nie zawiodłem się, bo szybko znalazłem kolejny błąd w sposobie w jaki został uwzględniony ciąg silników:
155: az = (cos(pitch(i))*cos(p)*n-1.)*9.81 +az_thr(i) ; [m/s^2]
gdzie az to przyspieszenie pionowe, a az_thr- składowa pionowa przyspieszenia od siły ciągu silników:
114: az_thr = sin(pitch)* thr/78. ; [m/s^2] vert. acc., assuming 78 ton mass
Czy wzór z linii 155 jest poprawny? Otóż nie, bo gdy samolot leci poziomo, to przyspieszenie pochodzące od siły ciągu silników jest już uwzględnione we wskazaniu akcelerometru (symbol n). We wzorze trzeba ująć tylko tą część tego przyspieszenia, której akcelerometr nie zmierzy, a dzieje się to wtedy, gdy występuje przechylenie p. Poprawny zapis to:
155:az = (cos(pitch(i))*cos(p)*n-1.)*9.81 +az_thr(i)*(1-cos(p)) ; [m/s^2]
Po wprowadzeniu do programu opisanych powyżej poprawek, wyniki zmieniają się na tyle znacznie, że teza o ich zgodności ze smoleńską rzeczywistością jest nie do utrzymania. Skupię się na dwóch uzyskanych wykresach.
Rys.2. Teren i profile lotu PLF 101
Wykres oryginalny

Wykres po poprawieniu błędów
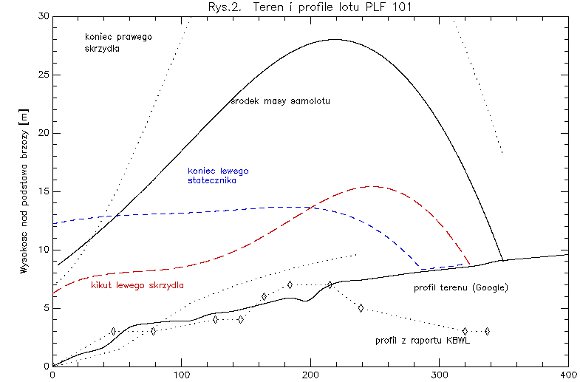
Widać, że lewy statecznik i lewe skrzydło uderzają w ziemię ponad 20 metrów wcześniej. Model jest bardzo wrażliwy na zmiany przebiegu przyspieszenia, co trzeba wziąć pod uwagę w kontekście komentarza z programu you-know-who, które uczyniłem mottem mojej notki.
Rys.8. Mapa lotu PLF101, odłamków i obiektów napotkanych w terenie
Wykres oryginalny

Wykres po poprawieniu błędów

O ile zgodność ze ścięciami drzew przy autokomisie jest lepsza, to całkiem ginie związek ze śladami na ziemi - bruzdy, które miały być ryte przez lewy statecznik i lewe skrzydło.
Wnioski ogólne
Peemka w swojej notce (http://pmk.salon24.pl/431071,analiza-symulacji-dynamicznej-prof-pawla-artymowicza ) wykazał, że model przyjęty przez you-know-who jest wątpliwy. Okazuje się również, że i w samym zapisie tego modelu są błędy, które zmieniają zasadniczo końcowe wyniki. Z drugiej strony, jestem przekonany, że gdyby you-know-who zauważył te błędy na etapie tworzenia swojego programu, to z łatwością mógłby skorygować inne parametry by osiągnąć lepszą zgodność ze smoleńską rzeczywistością. Nie jest bowiem prawdą, że program zawiera mało wprowadzanych ręcznie danych. Jego podstawą jest kilka funkcji aproksymujących przebieg parametrów lotu w zależności od czasu, nie wynikających bezpośrednio z przyjętego modelu. Jak wykazano to dla przyspieszania, model jest bardzo wrażliwy na postać tych funkcji.

