Do żelaznego repertuaru popkulturowego ujęcia mechaniki kwantowej należy łączenie zasady nieoznaczoności z możliwością wykonywania tzw. pomiarów jednoczesnych. Od razu napiszę, że w rzeczywistości oba aspekty kwantologii nie mają ze sobą wiele wspólnego. Przynajmniej bezpośrednio. Łączą je w pewnym sensie tzw. relacje komutacji, ale poniżej zobaczymy, że nie tak, jak chcieliby domorośli edukatorzy, którzy zaraz po opisaniu przygód kota podłączonego do rozpadającej się cząstki, zabierają się za zasadę Heisenberga.
Czym są wspomniane relacje komutacji? Tu trzeba dowiedzieć się, jak w danym stanie liczy się nieoznaczoność obserwabli. W miarę prosto omówione jest to w notce „O czym mówi zasada nieoznaczoności”. W notce tej piszę też o komutatorze dwóch obserwabli. Sposób komutowania – owe relacje komutacji – spotkamy właśnie w sformułowaniu zasady nieoznaczoności:
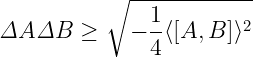
Równanie mówi o dokładności pomiarów A i B jaką można uzyskać przy zadanym stanie. Wielkość [A, B] = AB – BA, to inaczej komutator, czyli miernik nieprzemienności obu operatorów. Jeśli [A,B]=0 to mówimy, że obie obserwable komutują (są przemienne).
Pora teraz przeanalizować jakieś jednoczesne pomiary dwóch wielkości, co to albo komutują, albo nie, i zastanowić się jak się ma do nich zasada Heisenberga. Zauważmy tylko, że postulat o prawdopodobieństwie mówi jedynie, jakie są szanse uzyskania wyniku, gdy dokonujemy pojedynczego pomiaru obserwabli na stanie, więc o jednoczesności niech wypowie się praktyka.
Pęd i położenie
Konkretna, liczbowa postać prawej strony zasady nieoznaczoności zależy od stanu ψ. No bo prawa strona nierówności czyli
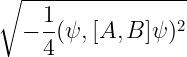
jest różna dla różnych ψ. Może być na przykład zerowa, nawet gdy [A, B]≠0. Wyjątek, ale za to dość ciekawy, stanowi przypadek, gdy komutator A i B jest równy stałej.
Tak właśnie jest dla operatorów położenia i pędu. Ich komutator jest równy [x,p]=iħ, więc zasada nieoznaczoności sprowadzi się do prostej postaci:
ΔxΔp ≥ (1/2)ħ
Zauważmy: ani położenie, ani pęd nie mogą mieć wektorów własnych. Gdyby było inaczej Δx lub Δp mogłoby być wtedy równe zero, a to przeczyłoby powyższej nierówności. Nawiasem mówiąc to bardzo ciekawe spostrzeżenie: Δx>0 oraz Δp>0 dla jakiegokolwiek stanu.
Ale wróćmy do pomiarów. Wyobraźmy sobie doświadczenie z dwiema szczelinami: źródło produkuje elektrony, które po rozdzieleniu na dwie wiązki, lądują na ekranie. Elektrony wypuszczane są jeden po drugim, żeby sobie wzajemnie „nie przeszkadzały”. Co uzyskamy ze zmierzania miejsca w którym objawił się jeden elektron? Oczywiście jedno z możliwych położeń w stanie ψ. Jeśli nawet pomiar taki spełnia formalne wymagania, to raczej nikt nie uzna osiągniętego wyniku za satysfakcjonujący. Innymi słowy nie dowiedzieliśmy się prawie nic na temat „położenie cząstki w stanie ψ”. Musimy zrobić wiele pojedynczych pomiarów na takim samym stanie, żeby móc powiedzieć cokolwiek mądrego o średnim położeniu i jego nieoznaczoności. A jak mamy dużo pomiarów położenia, to pojawią się prążki interferencyjne. Z odległości między nimi obliczymy długość padającej fali, a z niej wartość pędu. Czyli „przy okazji” pomiaru położenia zmierzyliśmy również pęd.
Jak widać ograniczenia nakładane przez zasadę nieoznaczoności nie zabraniają wykonywać jednoczesnych pomiarów. Przeciwnie: często zdarza się, że pomiar pędu odbywa się właśnie poprzez pomiar położenia prążków interferencyjnych, kątów rozproszenia padającej wiązki czy w końcu promienia krzywizny toru w polu magnetycznym. Wbrew obiegowej opinii, pomiary położenia i pędu dokonują się jednocześnie. W zasadzie to ten sam pomiar.
„Jednoczesne” pomiary
Załóżmy teraz, że mamy przypadek obserwabli komutujących, czyli że [A,B]=0. Jednym z ogólnie formułowanych sądów w kwantologii jest zdanie, że w tych właśnie przypadkach można tak sobie ułożyć pomiar, by dostać zarówno dokładną wartość A jak i B – za chwilę uściślimy to stwierdzenie, bo w ogólności nie jest to prawda. W notce „Jaki moment pędu ma orbital” możemy się przekonać, że jest to dość nietrywialna cecha układów kwantowych. Pisałem tam, że dokonując pomiaru energii układu elektronów w atomie umieszczonym w zewnętrznym polu magnetycznym, możemy obliczyć ich całkowity moment pędu i jedną z jego składowych.
Stąd właśnie wzięło się to całe opowiadanie o jednoczesności pomiarów. Ale wyjątkowość tej sytuacji nie polega na tym, że można wymyślić sobie doświadczenie, w którym jednocześnie poznamy wartości trzech obserwabli, bo tak naprawdę mając jeden atom, który wyemitował jeden foton (prawie) niczego się nie dowiemy. Wyjątek polega na tym, że możemy dostać wyniki bez dyspersji – nieco dalej wyjaśnię w czym rzecz.
Żeby móc coś powiedzieć o momencie pędu elektronów w atomie, jeden pomiar energii[1] (detekcja jednego fotonu) nie wystarczy. Potrzeba zmusić do emisji wiele atomów, żeby mieć informację o wszystkich możliwych energiach. Dopiero wtedy możemy wnioskować o całkowitym momencie pędu i wybranej składowej. Czyż nie przypomina to poprzedniego przykładu z niekomutującym położeniem i pędem?
Teraz o co chodzi z tą dyspersją: Jeśli obserwabla A ma stany własne, to nieoznaczoność pomiaru A w takim stanie – czyli inaczej dyspersja – może być dowolnie mała. Piszemy, że ΔA = 0. W tym miejscu objawia się relacja komutacji – jeśli obie obserwable A i B mają stany własne i do tego komutują, to znaczy że istnieją stany dla których równocześnie ΔA=0 i ΔB=0. Czyli możemy sobie tak ułożyć serię wielu pojedynczych pomiarów, że dostaniemy dokładne wyniki pomiarów zarówno dla A jak i B. Dla odpowiednio wybranych stanów!
Wracając do przykładu z elektronami w atomie – operatory: energii, kwadratu momentu pędu i jednej z jego składowych komutują ze sobą parami, co oznacza, że możemy zmierzyć bez dyspersji zarówno możliwe energie, jak i możliwe całkowite momenty pędu, jak i odpowiadające im możliwe składowe w wybranym kierunku.
Zauważmy jednak, że komutacja dwóch obserwabli wcale nie zapewnia istnienia stanów, w których ich dyspersja będzie zerowa! Pomimo, że położenie komutuje z energią potencjalną:
[ x, V( r ) ] = 0
nie znajdziemy stanów[2] dla których Δx=0 czy ΔV=0, czyli takich dla których da się dokładnie określić położenie i energię potencjalną.
I na koniec ciekawostka: w przypadku komutowania obserwabli, sama zasada nieoznaczoności staje się trywialna – nie niesie ze sobą żadnych dodatkowych treści. Albowiem iloczyn dwóch nieujemnych wartości zawsze musi być większy lub równy zero: ΔAΔB≥0.
* * *
Przykłady omówione w notce należą do „tradycyjnych” pomiarów kwantowych. Robimy ich całą serię i analizujemy wyniki. Ciekawym byłoby zastanowić się, jak to się ma do coraz częstszych eksperymentów przeprowadzanych na pojedynczym układzie. Nie czuję się jednak kompetentny, by zabierać tu głos.
[1] Nawiasem mówiąc: ten pojedynczy pomiar nie realizuje postulatu o prawdopodobieństwie – pisałem o tym komentując listę postulatów – trochę psuje to uroczy obrazek aksjomatyki kwantologii nierelatywistycznej.
[2] Dokładniej rzekłszy ΔV=0 jest możliwa do uzyskania, jeśli energia potencjalna będzie w pewnych obszarach stała i nośnik funkcji falowej ograniczać się będzie do jednego z takich obszarów. Jest to jednak przypadek dość patologiczny, bez przełożenia na empirię.







Komentarze
Pokaż komentarze (4)