Względem fotonu?

Kiedyś spotkałem się z pytaniem, jaka jest prędkośc fotonu względem drugiego fotonu, jeśli lecą naprzeciwko siebie, albo nawet jeden za drugim? No i odpowiedź jest o tyle prosta, co nieintuicyjna.

Zacznijmy od tego, że w STW, bo to o niej będę pisał, operuje pojęciem układu inercjalnego. Układ odniesienia, czyli zestaw czterech funkcji, który każdemu punktowi czasoprzestrzeni, przyporządkowuje cztery liczby - trzy określają położenie a jeden współrzędną czasową. Żeby przepisać coś z jednego układu do drugiego trzeba stosować tzw. przekształcenia Lorentza (lub nieco ogólniejsze Poincarego). Jeśli jeden z układów uznamy za inercjalny, to wszystkie inne inercjalne dostaniemy przez zastosowanie owych przekształceń.

Jak odpowiedzieć na pytanie jaka jest prędkość ciała A względem ciała B? Otóż znajdujemy układ współrzędnych w których B jest nieruchome i patrzymy jaka jest w nim prędkość A. No to teraz nie zostało nic innego, jak znaleźc inercjalny układ wpsółrzędnych dla fotonu. No i z tym jest kłopot.

W STW dla fotonu nie istnieje inercjalny układ odniesienia. Otóż nie ma takiego przekształcenia Lorentza, które dawałoby układ w której foton mógłby być nieruchomy. Nie do końca to zgadza się z codziennym doświadczeniem, ale można to dość prosto wykazać. Oto wzór na transformację Lorentza z jednego układu współrzędnych (x, y, z, t) do drugiego (x', y', z', t'):

x' = γ(x - vt)
y' = y
z' = z
t' = γ(t- (vx)/c²)
gdzie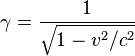

Transformacja opisuje dwa układy poruszające się względem siebie w kierunku X z prędkością v. Aż korci, żeby za v wstawić c. No i po postawieniu wyjdzie skucha. Wzór na gamma będzie miał w sobie dzielenie przez zero. Chwila zastanowienia i od razu będzie jasne, że wartość parametru v musi spełniać warunek -c < v < c.

Pamiętamy szkolne zadania ze znajdowaniem dziedziny, gdzie np. dla funkcji f(x)=1/x wykluczaliśmy x=0 z dziedziny funkcji. Tu jest cokolwiek podobnie. Transformacje mają sens tylko dla prędkości układu mniejszych od prędkości światła.

No dobra, ktoś powie, układ współrzędnych, to zestaw czterech funkcji, na przykład taki:

x' = x - ct
y' = y
z' = z
t' = t

W takim układzie foton "stoi". Tylko, że ten zestaw funkcji nie ma dobrej interpretacji fizycznej. To znaczy wyrażenie x - ct nie opisuje czegoś, co miałoby własności położenia w układzie inercjalnym.

Powyższe roważania wcale wcale nie oznaczają, że nie mogą istnieć obiekty (np. fotony), które prędkość światła mają. Mogą, tylko nie da się z nimi związać inercjalnego układu odniesienia. Co więcej, jeśli coś porusza się w jakimś układzie inercjalnym z prędkością c, to w każdym innym też ma taką prędkość. Jest to oczywiście sprzeczne z codzienną intuicją, ale zgodne z wieloma doświadczeniami. W szczególności z całą elektrodynamiką, z której owe przekształcenia Poincarego czy Loretza wynikają. Postulat o jednakowości prędkości światła we wszystkich układach wynika właśnie z równań Maxwella.

Ponieważ dla fotonu nie ma układu odniesienia, trudno mówić, że cokolwiek porusza się względem niego. To nie tylko słowa: nie można określić prędkości latarki względem fotonu, co nie jest tak bolesne, bo prędkość fotonu względem latarki jest do określenia (równa c). Bardziej ciekawe w tym kontekście jest to, że pytanie "jaka jest prędkość fotonu względem innego fotonu?" jest bezsensowne w STW. Bo mogłoby się zdawać, że jeśli dwa fotony lecą w przeciwnych kierunkach to prędkość jednego względem drugiego mogłaby być równa 2c. Albo że jak fotony lecą w tym samym kierunku, prędkość ta wynosi 0. Ale nic z tego.

Może to się wydawać dziwne, ale w ciele STW tak właśnie jest.

Powyższa notka jest tak naprawdę zestawieniem komentarzy, które popełniłem w notce blogera Ludwiczek69 pt: i co wy na to płaszczaki?