Al.K Al.K
288
BLOG

Szyfry (1). Algorytm RSA a liczby Mersenne’a

Al.K Al.K Nauka Obserwuj temat Obserwuj notkę 3
BLOG

MM&AlK

Po ponad rocznej przerwie wracam do nie dokończonego tematu liczb Mersenne’a… Najpierw parę zdań o najpopularniejszym asymetrycznym, algorytmie szyfrowania danych - o RSA, znanym od prawie pół wieku jak to zauważył @ Almanzor w komentarzach do poprzedniej notki…   

Algorytm RSA opracowany został w 1977 roku przez Rona Rivesta, Adi Shamira i Leonarda Adlemana. Asymetryczność szyfrowania polega na stosowaniu dwóch kluczy: 
•  publicznego - udostępnionemu każdemu, będącego iloczynem dwóch dużych liczb pierwszych.
• prywatnego - tajnego klucza, znanemu jedynie właścicielowi, służący do odszyfrowania informacji zaszyfrowanej kluczem publicznym.

Istotą algorytmu RSA jest matematyczny problem rozkładu wielkich liczb na czynniki pierwsze. Aby złamać szyfr RSA należy rozbić klucz publiczny na dwie liczby pierwsze będące jego dzielnikami. Znajomość tych liczb pozwala rozszyfrować każdą informację zakodowaną kluczem prywatnym i publicznym. Jako przykład trudności w rozkładaniu dużych liczb na czynniki pierwsze podawany jest, zarówno w internecie jak i pismach komputerowych, następujący przykład:

„Klucz 128 bitowy. Pierwiastek jest liczbą 64 bitową. W zakresie od 2 do 264 co druga liczba jest nieparzysta, zatem jest ich około 264 / 2 = 263. Ponieważ interesuje nas tylko górna połówka, to ilość liczb do sprawdzenia jest dwa razy mniejsza, czyli wynosi
 263/ 2 = 262.  Ile czasu zajmie naszemu superkomputerowi sprawdzenie podzielności przez około 262 liczb, jeśli w ciągu 1 sekundy wykonuje on miliard sprawdzeń? Odpowiedź brzmi: zajmie to około: 
 262/109 = 4 611 686 018 sekund = 76 861 433 minut = 1 281 023 godzin = 53 375 dni = 146 lat.”

To wszystko wiadome. Szyfrowanie algorytmem RSA jest bardzo popularne – wystarczy sprawdzić certyfikaty np. przeglądarek internetowych… Stosowany szeroko w podpisach cyfrowych itp.

… Jeżeli jest to tak pięknie, to dlaczego rząd Stanów Zjednoczonych zabronił stosowania RSA w instytucjach rządowych  i administracji?

… Wróćmy zatem do podstaw… Znalezienie dużych liczb pierwszych nie jest sporawą prostą. Dla znalezienia dużych liczb pierwszych wykorzystywany jest test pierwszości Lucasa-Lehmer’a lub test pierwszości Millera-Rabina. 
Test Lucasa-Lehmer’a oparty jest na twierdzeniu mówiącemu, że: 
„Liczba Mp = 2p – 1, gdzie p jest liczbą pierwszą > 2, wtedy i tylko wtedy jest liczbą pierwszą, gdy jest dzielnikiem (p – 1)- go wyrazu ciągu s1, s2, ... określonego przez warunki:
                                                s = 4 oraz sn + 1 = sn2 – 2 dla  n = 1, 2, ... „ 
                                                                                    W. Sierpiński, Teoria liczb, Część II, str. 381 – 385.

Pierwotne duże zainteresowanie bardzo dużymi liczbami Mersenne’a, dla celów kryptografii, związane było z ciekawą własnością tych liczb, o której już wspominałem. Liczba 2p w zapisie dwójkowym, to liczba jeden z ciągiem p zer. Liczba 2p – 1, to ciąg jedynek. Taki zapis cyfrowy pozwala bardzo szybko badać bardzo duże liczby testem Lucasa-Lehmer’a (test pierwszości). 
To z kolei pozwala znajdować bardzo duże liczby pierwsze... Szybko okazało się jednak, że liczby Mersenne’a nadają się tylko i wyłącznie do znajdowania dużych liczb pierwszych...

Odpowiadając na komentarz @ Almanzora, do ostatniej notki, podałem liczbę będącą iloczynem dwóch liczb Mersenne’a z propozycją rozkładu tej liczby na czynniki pierwsze jako pewną formę zabawy. Jest to liczba mająca 3 187 cyfr, a więc liczba ok. 10 580 bitowa. Liczba o 31 cyfrach, to liczba 100-tu bitowa, o 302 cyfrach, to liczba 1 000 bitowa, a o 3 011 cyfrach, to liczba 10 000 bitowa. Liczba 1 000 000 bitowa, to liczba o 3 010 300 cyfrach.  Duże liczby przytłaczają swą wielkością

Przeliczanie w jakim czasie liczbę rozłożymy na czynniki pierwsze, w sposób opisany powyżej, traci sens nie tylko z uwagi na wielkość liczby. Oto podana liczba N. 
5052823159421964767749871256460848515267033232493063467013144933414086718726
9939709160666271743998482919541143632501327204068954084367410501167896706056
9698967271069307414952284824132580987874922733977291469130396356960728494712
1948385749459994231238468628788878208325073672729895841047171019004484008606
7129520536838795787492514923681629940207838600012734491676534684477734809071
9504686801248412920627591150983950648462632899757972553447878997225854725128
4606999336511569109332182058239477996810425269163485188607572594870669105146
4224963505135795631744803479165020937681108672745265118160904506093449832593
6097080922190538131646200898904126689043246799652943584916432758802836022636
7447177564347307961988763808254365737543792476875046331058004081555778706087
7655240304545744043943038802414142653094061734373062391113613332644684175508
9258889862656947371989584501318021250076799023828972125614546821541563094719
3791865178856064522547357834572567214087388096946370357848848772052413814550
1301755697596905659290657154512632234924997451689599291226065231431517018004
3290851479716707011026550913624606594265443380606643880891075065156245754478
3206707685998916744294608900474082566867268228850100683968107981134943594946
0972109794914283850032067800659691530941955330583558849782413915050277407252
0551542193049429706194160320413948438974383325014872683811933597676548727438
1715425808731489866306866260604188655339241089370537240638930820828768325865
0087254051598718908213677185978151625248175253985204249616368245900479345596
9675428898153239679885345369953849577128019508454427910912040148304633309490
5755772970470723235189102672502956493623546536173679181955021760613566079820
7331189201313121393542362201105437176330230799372571183167410037472920107808
5094046658983026214987566214470175183100083743601204821109198208856593003562
7091103236387623583572495875586223071437741772704039420617628767384344800695
7479290622952901089849693738989134161563060687334929537631827643091552120272
9734357502761177408214517290701655840818406063448546683343014466223354206700
9131027277560434303869557857868971310681530596842782165742458176610636536202
5279974075091306082019993949171806808068926606990679150288458042744968179458
8692030773618190727830081964903375969730193024778210358759884412259111118808
1686533868982448414498526920678543610091192270777868228374298566075986705370
7708305029339897660935042756104663740612937813354928701813652473032341824412
0332498391670720567185985582210750484758398415766836615166347780512095371045
0226762534405610549021020828167038673836650378890998083448098644684173751684
1233239578759961551029967007552490224713881502467983735925851826538243871525
6004873156728957790190338919612587187232115937562017683067303254124256189159
2461530247924997683839639734583528086068572795984786540289252444757824978730
6423625663179829686452558447672451347815004402871592333380377465268523724598
6219028261222306941297289258136075778484560574902432094265421849709071729021
4950685589485682335504940578051305722760699504502383158868328404689271627012
1820507480967415822850161849439807516403726057268319661330170707264117700801
73964762059518528046524325121386662786300107459269285234752295584923649
Jest to jedna z mniejszych liczb, będących iloczynem liczb Mersenne’a. Czy będziemy poszukiwać czynników iloczynu setki miliardów lat, a więc dłużej niż trwa nasz wszechświat? … Jak ją rozłożyć na czynniki pierwsze?  

Piszemy najbardziej banalny programik w SageMath (jest to program dla szkół). Do programu wstawiamy rozkładaną na czynniki pierwsze liczbę N, natomiast za wartości n, m przyjmujemy liczbę mniejszą od połowy ilości bitów tej liczby, czyli mniejszą 
od 10 580/2 . Czas poszukiwań czynników będzie zależny od liczb, wstępnie przyjętych jako wartości początkowe.

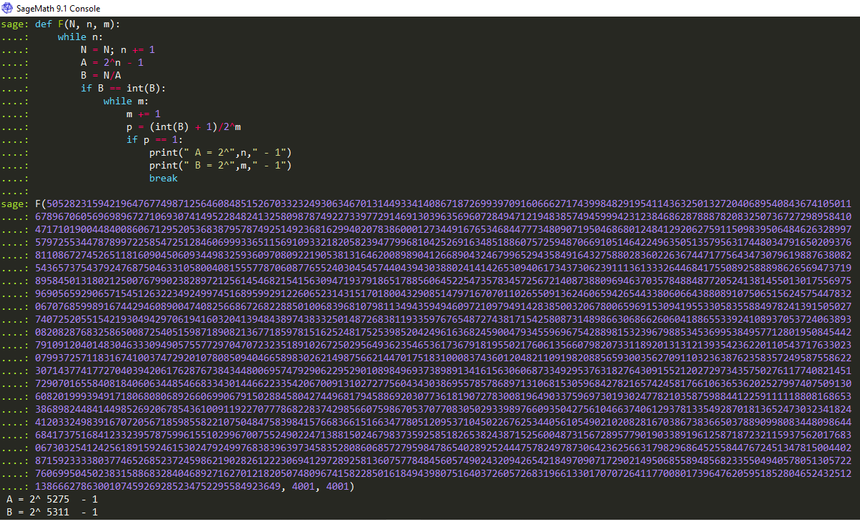
image

Po kilku sekundach, w wyniku otrzymamy:

                                             A = 25275 – 1;       B = 25311 – 1.   Zatem:    N = (25275 – 1) ( 25311 – 1).

Do programiku możemy wstawić praktycznie dowolną liczbę N, będącą iloczynem liczb Mersenne’a i taką, jaką jest w stanie przetworzyć komputer. Tylko pytanie… Jak praktycznie korzystać z klucza publicznego, który ma np. ponad 3 miliony cyfr i który można złamać po kilku minutach?

To tylko jedna z pierwszych przyczyn, która odpowiada na pytanie dlaczego rząd USA zabronił stosowania RSA… A co z liczbami pierwszymi otrzymanymi z testu Millera-Rabina? … O tym w następnej notce.

(w oparciu o ebook Zabawy z Pitagorasem, Fermatem i Goldbachem).




Al.K
O mnie Al.K

Nowości od blogera
Udostępnij Udostępnij Skomentuj3

Komentarze

Pokaż komentarze (3)

Inne tematy w dziale Technologie