MM&AlK
Szyfry (2). Algorytm RSA i test Millera – Rabina
W kryptografii, dla znajdowania dużych liczb pierwszych, stosowany jest test pierwszości Millera-Rabina opracowany w 1975 roku, oparty na twierdzeniu:
Niech p będzie nieparzystą liczbą pierwszą zapisaną jako p = 2nd + 1, gdzie d jest liczbą nieparzystą. Wtedy dla dowolnej liczby naturalnej k leżącej w przedziale <2, <i>p – 2> ciąg Millera-Rabina kd, k2d, k4d, ... , k2(n – 1)d, k2nd(mod p) kończy się liczbą 1.
Znajdowanie dużych liczb pierwszych testem Millera-Rabina, dla celów kryptografii, wymaga dużej interwencji w proces generowania list pierwszych (lub liczb o bardzo dużych dzielnikach). Generowane liczby nie są liczbami losowymi…
Wspominałem, w jednej z notek, że gdyby wygenerowane klucze publiczne N, były iloczynem liczb pierwszych postaci p1 = 2na + 1, p2 = 2mb + 1, gdzie a ≠ b to liczby nieparzyste i n < m to dla danej długości klucza N (dla danej ilości cyfr), przy dużych wartościach n byłyby bardzo podatne na złamanie.
Przykłady.
Dana jest liczba N =
626328894450604717615464548914168519278753861412012892976671107372636861835
975724346506860534214000783060863194382201867969606105289394610097572716174
840586143808233622081900985014793952563114296010624120350900438696175968878
547263268578886906953305508991705764487650717026212532625396970038374374202
501696846847649300578208569077551516574946259979152117048025885208586940669
527692698792384781518891510285322419077865242897655061861293951061253565511
530558809217624813698118932791917462396979058543927133819716012242266326098
883111703527674993873493917626410850830075177656528437701046877793640335495
992623788404358892321133575785494505249616170819422923534837965807038136689
018102360799010260342796806071610898719270196267309534055323320074794949476
210958425492693259968565323781669781955037614133976684211014101506093571267
518240899099841751224846035196643271813287987807262172550962651559999390272
512502793396365723578280162832865556503768993819924614889131603761872863162
640334817920368590259410850381500422664831840875584745344470016761614456547
525916390661412616821939620301565410199338108999904480036316183410716610061
467604560070276914006124495849134226734526653536558648198873538544127753880
701149795152973053625150075355802453684030351537009559254620901380659186875
62754703515784839169.
Liczba ma 1295 cyfr. Jest to liczba 4 300 bitowa. Aby rozłożyć liczbę na czynniki, napiszemy kolejny bardzo banalny program w programie SageMath (jak np. poniżej).
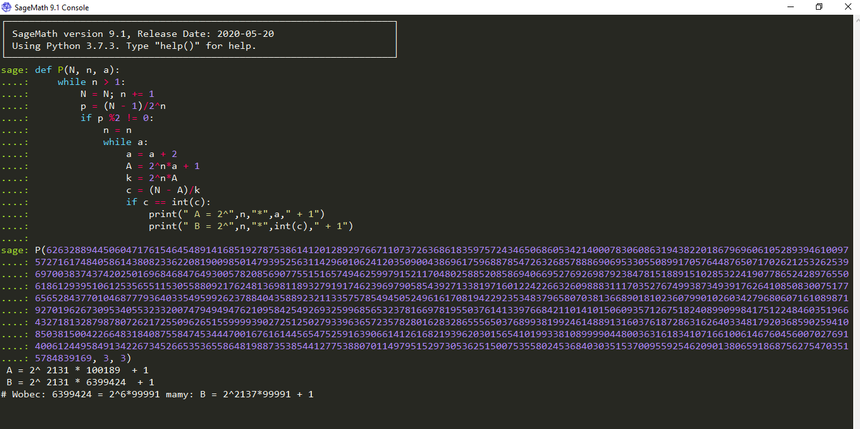
Otrzymane liczby, to:
A = 22131 × 100 189 + 1 ; B = 22131 × 6 399 424 + 1 = 22137× 99 991 + 1.
Znacznie trudniejszy jest rozkład liczby na czynniki gdy wykładniki potęg liczby 2 są równe;
p1 = 2na + 1, p2 = 2nb + 1, gdzie a ≠ b są liczbami nieparzystymi. Przykład poniżej...
Dana jest liczba N =
683005966628536109118799763155791544787432326555622389379812904983020710467
142064702610998920205751462527509240248116919704349012469771338607299769687
056545135731531057210609012366213266113565788254953140455254609018480113060
375662437460008186957442565373855863084257643646801230173744780694009895080
864542036912920756590498474698874556867194972706358494137430701760935411817
975298998121963477704563114754850302321760417684758190515808798188649092585
165251140206216440617600462318628466205277559943118773268656963071406408181
908766798061756588400980846132805144748309753764724936274071939799035138684
300175031866652019605975359760226489983621327821269952662647190165879401322
9057.
Jest to liczba mająca 679 cyfr, a wiec liczba 2 300 bitowa. Poszukując czynników liczby należy od liczby N odjąć liczbę 1 i dzielić otrzymaną liczbę przez największą potęgę liczby 2.
Jest więc: k = (N – 1)/2m, gdzie k jest liczbą nieparzystą. Dla liczby k znajdujemy m = 1115. Następnie wykorzystujemy "własny" programik, przyjmując dla wzoru nx = m – x kolejno:
x = 1, 2, 3, 4. Dla x = 1, 2, 3 nie znajdziemy rozwiązania.
Dopiero dla x = 4 mamy n = n4 = m – 4 = 1 111. Jako rozwiązanie otrzymujemy:
A = 21111 × 88129 + 1,
B = 21111 × 100151 + 1.
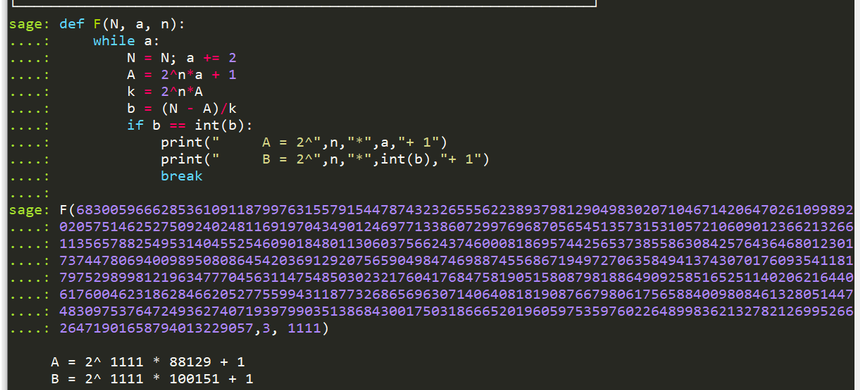
Możliwości tych banalnych programików jest ograniczona nie wielkością wykładnika potęgowego ale iloczynem liczb a, b w strukturze wewnętrznej liczby. Pamiętać należy o możliwości posiadanego sprzętu tj. o wielkości zasobów pamięci przeznaczonych dla liczb zmiennoprzecinkowych (przy Windowsie liczby mogą posiadać max 15 cyfr… Przy większych liczbach otrzymamy błędne wyniki) .
Przykłady powyższe mówią, że stopień trudności rozkładu liczby na czynniki pierwsze zależy od struktury wewnętrznej liczby a nie od jej wielkości. Liczby pierwsze p = 2na + 1 generowane testem Millera-Rabina nie mogą posiadać dużych wykładników potęgowych n, i zbyt małych liczb nieparzystych a. Generatory liczb pierwszych muszą być odpowiednio zaprogramowane (liczby pierwsze nie są liczbami losowymi) – wymagają interwencji programisty. Jeśli otworzymy certyfikaty np. przeglądarek internetowych, to możemy łatwo się przekonać, że certyfikaty są praktycznie wszystkie liczbami postaci 216a + 1…
Ustalając zasady wyznaczania liczb pierwszych mamy możliwość poznania struktury generowanego klucza publicznego… Fakt ten uzależniał administracje rządowe od urzędów certyfikujących i programistów zatrudnionych przy certyfikacji, którzy są w stanie złamać każdy klucz publiczny jaki wygenerowany został w tej firmie. To jest druga z przyczyn odpowiadająca na pytanie dlaczego rząd USA zabronił stosowania RSA w administracji rządowej. Rząd USA nie chciał być zakładnikiem korporacji informatycznych…
Najtrudniejsze do rozkładu są liczby będące iloczynami dużych liczb o małym wykładniku potęgowym, a więc liczby postaci 2a + 1, ale czy zawsze?… O trzeciej przyczynie stosowania zakazu - w kolejnej notce…
(w oparciu o ebook Zabawy z Pitagorasem, Fermatem i Goldbachem).
Inne tematy w dziale Technologie

