Statki kosmiczne Bella-Einsteina a fizyczne zbliżenie

Einstein doradza: by się nie oddalać, należy się zbliżać. Ta rada jest szczególnie ważna w obecnej chwili. Wymagają od nas zachowania stałej odległości jeden od drugiego. Jednak, zgodnie ze szczególną teorią względności Einsteina, gdy zachowujemy stałą odległość, to się oddalamy. Możemy to skompensować nieustannym zbliżaniem. Zobaczymy to na wykresie przy końcu notki: dwie linie świata zbliżają się do siebie, by zejść się asymptotycznie ze sobą i ze światłem. Zbliżają się po hiperbolach o różnych promieniach krzywizny. I to jest konieczne, bez zmiennej krzywizny więź je łącząca się zerwie. Tak wynika ze szczególnej teorii względności, również tej alternatywnej, z eterem.

A konkretnie: znany jest tzw. Paradoks Bella o dwóch statkach kosmicznych. W roku 1976 John Bell opublikował artykuł p.t. “”How to teach Special Relativity” - “Jak uczyć szczególnej teorii względności”. Artykuł ten został potem przedrukowany w książeczce p.t. “Speakable and unspeakable in quantum mechanics” wydanej przez Cambridge University Press w roku 1987. Znajduje się tam na str. 67. W chwili gdy piszę tę notkę artykul ten można sobie ściągnąć stąd.

Bell proponuje by studentom postawić następujący problem do zastanowienia się nad nim.

W układzie inercjalnym obserwatora startują dwa identyczne statki kosmiczne. W chwili startu są oddalone od siebie o pewną odległość. Startują jednocześnie i w tym samym kierunku. Mają identycznie zaprogramowane napędy, tak, że poruszają się ze stałym własnym odczuwalnym przyśpieszeniem, mającym tę samą wartość dla każdego z nich. Połączone są ze sobą nicią.

Oto ilustarcja wzięta z dyskusji na physicsforums:

Pytanie brzmi tak: co się stanie z nicią? Bell pisze, że intuicja mu mówi, że nić się po pewnym czasie zerwie, bo odległość pomiędzy statkami się będzie zwiększać w wyniku efektów wynikających z transformacji Lorentza. I to pomimo tego, że w układzie obserwatora odległość pomiędzy dwoma statkami pozostaje stała.

Tak to wygląda na wykresie ich linii świata w przestrzeni Minkowskiego:

Wzięte z witryny Johna Baez, ze strony “Bell's Spaceship Paradox”.

Od czasu publikacji w roku 1976 na temat tego paradoksu napisano dziesiątki prac proponujacych różne interpretacje i różne podejścia do tego pytania. Sam Bell w swojej oryginalnej pracy pisze, że zadawał to pytanie wielu swoim kolegom-ekspertom w CERNie i zdecydowana większość odpowiadała, że nić się nie urwie. Choć potem dawali się przekonać, że może jednak się urwie:

This old problem came up for discussion once in the CERN canteen. A distinguished experimental physicist refused to accept that the thread would break, and regarded my assertion, that indeed it would, as a personal misinterpretation of special relativity. We decided to appeal to the CERN Theory Division for arbitration, and made a (not very systematic) canvas of opinion in it. There emerged a clear consensus that the thread would not break!

Nie będę tu wchodził w detale. Żadna ze znalezionych przeze mnie publikacji mnie nie satysfakcjonuje a sam mam inne plany aniżeli rozważanie tego właśnie sztucznie wymyślonego problemu. Jednak intuicja podpowiada mi, że dyskusja w witrynie Johna Baeza jest poprawna.

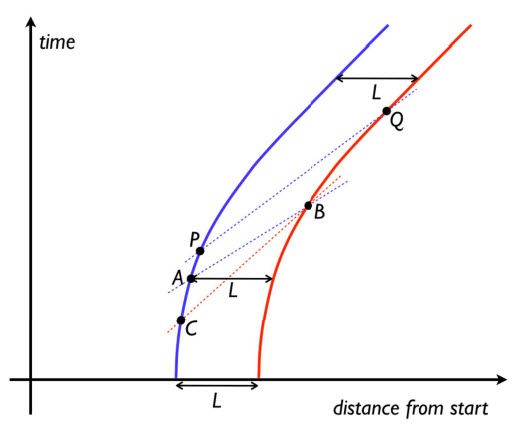
Pada tam także takie pytanie: Czy można zmienić ruch jednej z tych rakiet tak, że ta para będzie stanowić “układ odniesienia”, czyli tak by nić te statki łącząca nie zerwała się? I odpowiedź jest, że “tak”, że można. Jedna z hiperbol musi mieć odpowiednio większą krzywiznę. Towarzyszy temu taki wykres:

Widać tu dwie hiperbole zbliżające się asymptotycznie do siebie i do promienia światła. Istnieją teorie w których mamy nie tylko maksymalną prędkość, ale i maksymalne przyśpieszenie. Wtedy przy dużych dużych przyśpieszeniach szczególna teoria względności przestaje obowiązywać i te dwie hiperbole mogą się spotkać ze sobą w czasie skończonym.

A matematykę kryjącą się za takimi właśnie hiperbolami tworzącymi “układ” dyskutowałem w poprzednich notkach – patrz ostatni graf w notce z przed miesiąca p.t. Obroty i wiatr Minkowskiego