Jest sobie grupa Lorentza. To transformacje przejścia pomiędzy układami inercjalnymi. Jednak sa to transformacje globalne, i mało kto podaje jawne formuły na ich kwantową realizację, Matematyka jest tu uciążliwa. Dość skrzętnie omijana. Miast globalnych transformacji Lorentza wygodnie jest ograniczyć się do "infinetezimalnych generatorów" tych transformacji. Jeśli U(t) jest jednoparametrową grupą unitarnych transformacji, a tak symetrie są realizowane w fizyce kwantowej, to U(t)=exp(tX), gdzie X jest operatorem antyhermitowskim: X*=-X. W fizyce kwantowej używamy jednak zespolonych przestrzeni Hilberta, Tam mamy do dyspozycji urojone "i". Czemu akurat zespolonych? To wciąż wielka tajemnica. Niedawny artykuł donosi:
Imaginary numbers could be needed to describe reality, new studies find
By Ben Turner published 2 days ago
If standard quantum theory holds up, imaginary numbers are critical."
Mając do dyspozycji "i" zamieniamy X na iX. A ponieważ i*=-i, to teraz X w
U(t)=exp(iXt) (*)
jest hermitowski. A hermitowskie operatory mają rzeczywiste wartości własne interpretowane jako możliwe wyniki pomiarów, nazywa się je zwykle "obserwablami". Tak więc z każdą jednoparamtrową grupą wiążemy "obserwablę X, jak w równaniu (*). Nazywamy X generatorem naszej grupy symetrii. I tak generatory symetrii względem przesunięć identifikujemy z opratorami-obserwablami pędu Pi (i=0,1,2,3) (pomijam tu stałą Plancka potrzebną do tego by X było bezwymiarowe). Generatorami trójwymiarowych obrotów są operatory krętu, zwykle oznaczane Ji. To generatory obrotów wokół i-tej osi (i=1,2,3). Generatorami porywów są Ki. Nie mają ładnej i prostej nazwy. Grupa Poincarego, grupa niezmienniczości kwantowej cząstki swobodnej, cząstki kwantowej w czasoprzestrzeni Minkowskiego, ma więc w sumie 10 generatorów. Cztery to generatory przesunięć w przestrzeni i w czasie, trzy generatory obrotów, trzy generatory porywów. Jako operatory spełniają pewne związki komutacyjne. Są na ogół nieprzemienne, bowiem, na przykład obroty wokół różnych osi są nieprzemienne. Te związki możemy znaleźć na przykłąd w Wikipedii, z odnośnikami do podręczników. Oto te związki:
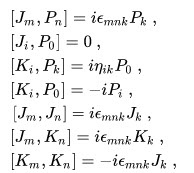
Ten tajemniczy epsilon onacza, że np [J1,J2]=i J3 itd. Cyklicznie. A te komutatory czytamy jako np. [J1,J2]=J1 J2 - J2 J1. W tej liście zabrakło tego, że pędy są wszystkie przemienne. To bardzo ważne. Bowiem przesunięcia w różnych kierunkach w przestrzeni są przemienne, a przesunięcia w przestrzeni sa przemienne z przesunięciami w casie.
To tyle w tej przedświątecznej notce. Teraz będziemy mogli wreszcie przejść do "inwariantów" od czego się ta seria zaczęła.
A z okazji Wigilii składam serdeczne życzenia wszystkim moim Czytelnikom. Przy okazji informuję, że kwantowy napęd kosmiczny (podróże w przestrzeni i w czasie) jest już w końcowej fazie jak to mówią "razrabotki". Wasz pilot od wczoraj już ma certyfikat.








Komentarze
Pokaż komentarze (22)