Notka dzisiejsza jest niejako rnaturalnym rozwinięciem notki "Foton zakręcony". Wariacją na jej temat. Dalej foton, dalej jego kwantowomechaniczny opis. Jak pisał Franz Kafka:
Wszystkie błędy ludzkie są niecierpliwością, przedwczesnym porzuceniem metodyczności, pozornym okalaniem pozornej sprawy.
"rozważania o grzechu, cierpieniu, nadziei i słusznej drodze".
Franz Kafka, Nowele i miniatury
Nie chcemy przedwcześnie porzucać nie do końca zgłębionego tematu. Nie chcemy pozornie okalać pozornej sprawy. Chcemy, jak to się mówi, byka chwytać za rogi, i nie puszczać, póki się nie podda, póki nie skapituluje. I ta notka jest początkiem serii notek, w której opowiem o tych fragmentach naszej będącej na ukończeniu pracy z AMS (aka Kleopatrą, patrz poprzednie notki "Skandal z "Fotonem"" i "Czas nadejścia w mechanice kwantowej"), które mogą byc przedstawione w sposób w miarę elementarny. Praca w fazie końcowej redakcji przed publikacją.
Sporo ta praca wymagała od nas rachunków. Pomagały nam w tym programy komputerowe Mathematica i Reduce. Kiedyś w dawnych czasach fizycy i matematycy potrafili przeprowadzać na papierze i w głowie niemal nieskończenie skomplikowane bezbłędne rachunki. Dziś te zdolności ludzkiego umysłu niemal całkowicie zanikły. Nie wyobrażam sobie dziś pracy bez wspomagania się przy rachunkach komputerem. Całą uwaga jest wtedy skoncentrowana na formułowaniu zadania w języku zrozumiałym dla maszyny. Potem już tylko naciskamy klawisz "Enter" i maszyna wypluwa wynik. Nad tym wynikiem trzeba potem jeszcze popracować by przedstawić go w zgrabnej formie. Ale nie ma już żmudnego sprawdzania cay w rachunklach czegoś nie pominęliśmy, czy nie pokręciliśmy znaków itd. Szukanie błędów w programie jest rzeczą czasem frustrującą, ale nie męczy. Jest wyzwaniem za które w końcu otrzymujemy nagrodę: prosty (często) wynik skomplikowanych obliczeń, takich, które zajęłyby nam tygodnie przy pracy głowy i rąk.
Zatem foton. Opisywany kwantowo mechanicznie. Opisujemy funkcją falową f. To f jest wektorem, ma trzy składowe. Wartości tych składowych sa liczbami zespolonymi, jak to zwykle w mechanice kwantowej. Nazywa się to "amplitudami prwdopodobieństwa", ale dla fotonu sprawy sie komplikują. Nawet jeśli są to "amplitudy prawdopodobieństwa", to nie bardzo wiadomo prawdopodobieństwa czego?. Bowiem fotony są nielokalizowalne w przestrzeni. I tego, nawiasem mówiąc, dotyczy nasza praca.
Margaret Hawton, fizyk (raczej fizyczka) opublikowała serię prac dowodząc, że foton jest lokalizowalny. Jej formalizm matematyczny jest dość skomplikowany i przegryźć się przez te prace nie było łatwo. Przegryźliśmy się z pomocą programów komputerowych i po skrupulatnej analizie znaleźliśmy błąd w rozumowaniach. To jest przedmiotem naszej pracy. Jednak zbyt to skomplikowane technicznie by to w sposób w miarę popularny opisać. Niemniej trochę da się wyjasnić w sposób przystępny nawet dla lcealisty.
Przypomnę co to jest foton. Krótko: foton to "jednocząstkowy stan kwantowego pola elektromagnetycznego", inaczej "światła". Klasycznie, niekwantowomechnicznie, pole elektromagnetyczne opisywane jest przez wektory natężenia pola elektrycznego i magnetycznego. Te spełniają równania Maxwella. Szczególnymi rozwiązaniami równań Maxwell są fale elektromagnetyczne.
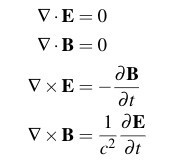
Równania Maxwell w próżni
Swiatło jednak wykazuje nie tylko własności falowe, ale także korpuskularne. By ten dualizm opisać potrzebna jest teoria kwantowa. Swiatło, to, popularnie, strumień fotonów. By opisać światlo potrzebna jest kwantowa teoria pola - elektrodynamika kwantowa.

By opisac pojedynczy foton wystarczy mechanika kwantowa, jednak relatywistyczna, zatem oparta na szczególnej teorii względności.
Dla opisu stanów kwantowych fotonu wystarczy jedna funkcja falowa f. Jednak okazuje się, że ta funkcja falowa to "trochę za dużo". Bowiem z analizy opartej o teorię grup (teorię reprezentacji grupy Poincarego) wynika, że przestrzeń takich funkcji zawiera nie tylko fotony (o spinie 1), ale także inne teoretycznie możliwe a praktycznie nieobserwowalne cząstki o masie zero i spinie 0. Ściśle mówiąc dla cząstek o masie zero mówimy nie o "spinie" a "skrętności", ale na razie nie będziemy się tym przejmować.
Stany fotonu opisywane są przez funkcje falowe f prostopadłe do wektora pędu. Dla każdego p≠0 mamy
p.f(p)=0.
Stany cząstek o spinie zero przez wektory równoległe do wektora pędu
f(p)=c(p) p,
gdzie c(p) jest funkcją skalarną o wartościach zespolonych.
Jaki jest związek funkci zespolonej f(p) z rozwiązaniami klasycznych równań Maxwella? Ten związek nie jest prosty, różni autorzy różnie to prezentują. Nie będziemyw to wchodzić. Zauważmy jednak, że by tego uniknąć, a także z tego powodu, że mechanika kwantowa fotonów jest specyficzna, trudniejsza od mechaniki kwantowej na przykład elektronów, lepiej, wygodniej, pracować w "przestrzeni pędów".
Wszystko wtedy staje się prostsze. Miast rozważać f(x), gdzie x jest punktem przestrzeni trójwymiarowej, rozważamy f(p), gdzie p jest pędem. Przejście od jednej reprezentacji do drugiej odbywa się przez (zespoloną) transformatę Fourira, znaną inżynierom i często używaną do analizy harmonicznej wszelkich drgań czy fal. Też nie będziemy w to wchodzić.
Główny problem na początek to : jak oddzielić niefizyczne stany o spinie 0 od fizycznych stanów o skrętności +1 i -1 (to fotony) kołowo spolaryzowane, prawo i lewo skrętne. Ogólnie foton jest superpozycją stanów o różnych skrętnościach.
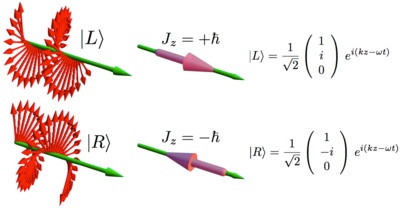
I tym się zajmiemy w następnej notce.







Komentarze
Pokaż komentarze (43)