Nemezis na horyzoncie

Czy życie na naszej planecie podlegało quasiperiodycznym masowym kataklizmom? W nauce nie ma w tej sprawie zgody. Jedni okresowość widzą i dokumentują, inni niczego nadzwyczajnego w tych samych danych nie dostrzegają. Co gorsze, nawet Ci co okresowe wyginięcia widzą, i to jasno, nie mogą dojść do porozumienia co do tego, co mogło być ich przyczyną. Wśród możliwych przyczyn wymienia się zderzenia Ziemi z bolidami, promieniowanie gamma wnikające z przejścia Układu Słonecznego przez szczególne obszary przestrzeni kosmicznej, działalność wulkaniczną, zmiany klimatyczne, naturalne cykle biologiczne, itd. itp. Dal przykładu oto grafik z publikacji usiłującej wykazać związek pomiędzy masowymi wyginięciami a oscylacjami Słońca względem płaszczyzny Galaktyki:

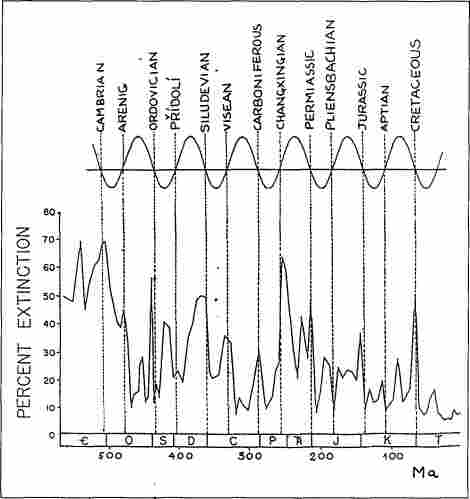
Działalność krytyków hipotez masowych wyginięć jest dość nieskomplikowana. Krytyk będzie szukał dziury w całym i zawsze ją znajdzie. Zazwyczaj taki krytyk zna się dobrze na pewnym fragmencie wiedzy i jest ignorantem w innych dziedzinach. Będzie więc ignorował fakty, których nie zna lub które mu są niewygodne. Skrytykować krytyka jest niezwykle łatwo, jeszcze łatwiej niż krytykowi skrytykować czyjeś hipotezy. Działalność krytyka najczęściej sprowadza się do argumentu typu: „Ziemia nie może być kulą, bowiem gdyby była kulą, to ludzie po drugiej stronie pospadaliby. Czyż to nie jasne?!” I laik, nie znający praw grawitacji taką krytykę przyjmie za logiczną i wielce słuszną i będzie ją z dumą powtarzał krewnym i znajomym.

Cóż, tak to już jest, są ludzie dostrzegający subtelne prawidłowości i są ludzie na nie ślepi. Są także ludzie widzący prawidłowości wszędzie, nawet tak, gdzie ich nie ma. W ten sposób życie ma wdzięk i urok. Dobrze, że spory w nauce nie rozpalają ludzi tak jak mecze piłkarskie – mielibyśmy bowiem walki kibiców na kije i kastety oraz palenie samochodów i witryn sklepowych.

Zainteresowanym sprawą wyginięć polecam przeglądowe książki A. Hallana i s-ki: „Mass Extictions and their Aftermath”, „Catastrophes and lesser calamities: the causes of mass extinctions”, „Great geological controversies”. Ale i od tych przeglądów nie należy oczekiwać zbyt wiele – każdy przegląd jest bowiem zabarwiony przekonaniami i poziomem wiedzy i rozumienia tej wiedzy przez jego autora.

W poprzednich dwóch notkach pisałem pisałem o hipotezie Nemezis – ciemnej towarzyszki Słońca. Aby móc tę hipotezę ocenić należy dokonać pewnych wyliczeń. Rachunki takie mają wartość niezależnie od tego czy hipoteza się potwierdzi czy nie. Jest to bowiem niezłe ćwiczenie z mechaniki nieba. Dziś wyliczymy, opierając się na założeniach o okresie, masie i peryhelium, parametry orbity Nemezis – wielkości obu półosi elipsy. Nie da nam to jeszcze pełnej informacji o ruchu, niemniej będzie stanowić punkt wyjściowy do dalszych obliczeń.

Nasze wyliczenia parametrów opierać się będą na dynamice Newtonowskiej – będziemy zakładać jej słuszność. Nie wiemy jak dobrze dynamika Newtona ma zastosowanie w przypadku Nemezis. Stosuje się nieźle do ruchu satelitów, komet i planet. Wiemy, że w przypadku planety Merkury mamy do czynienia że zjawiskiem bardziej złożonym – jej nietypowy ruch wyjaśnia się zwykle bliską odległością Merkurego od Słońca i mechaniką relatywistyczną. Na dużych odległościach możemy mieć także do czynienia z odchyleniami od mechaniki Newtona – znane są zjawiska uznawane przez niektórych fizyków i astronomów jako anomalne – niezwykłe kształty ramion wirujących galaktyk, anomalne zachowanie sond kosmicznych itd. W związku z tym otrzymane przez nas wyniki należy uznać za „orientacyjne”.

Do obliczenia geometrycznych parametrów orbity Nemezis zastosujemy trzecie prawo Keplera. Prawo to daje się wyprowadzić z mechaniki Newtona – my go wyprowadzać nie będziemy. Weźmiemy je z podręczników. Niestety w podręcznikach prawo to rzadko kiedy przedstawiane jest w pełnej formie. Najczęściej jest to forma zdegenerowana, dobra do rozważania ruchu księżyców wokół planet i planet wokół Słońca, ale nie nadające się do dyskusji układów podwójnych jak Słońce-Nemezis. Musiałem się dobrze naszukać w sieci zanim znalazłem trzecie prawo Keplera w jego pełnej postaci. A znalazłem w

Serwisie edukacyjnym Polskiego Towarzystwa Astronomicznego

Jest tam link do strony:

Ćwiczenia: Pomiary odległości we Wszechświecie

A strona ta jest w witrynie obserwatorium astronomicznego na Suhorze:

Obserwatorium astronomiczne na Suhorze

Obserwatorium astronomiczne na Suhorze (Suchorze) – obserwatorium zlokalizowane na szczycie Suhory (1000 m n.p.m.), na terenie Gorczańskiego Parku Narodowego. Jest najwyżej położonym obserwatorium astronomicznym w Polsce. Jest własnością i placówką badawczą Katedry Astronomii Uniwersytetu Pedagogicznego z Krakowa. Sporadycznie jest udostępniane zwiedzającym.

Obserwatorium zbudowane zostało w 1987. O wyborze lokalizacji zadecydowało położenie: dość duża odległość od najbliższej miejscowości, brak w pobliżu zakładów przemysłowych, a jednocześnie otulina leśna Parku. Ma zatem czyste i nieoświetlone niebo.

Obserwacje wykonywane są za pomocą 600 mm reflektora (teleskopu zwierciadlanego) Cassegraina firmy Carl Zeiss, Jena o efektywnej ogniskowej 7 500 mm. Obserwatorium posiada kamerę CCD SBIG ST10XME.

Od 1991 obserwatorium pracuje w systemie ogólnoświatowej sieci obserwatoriów, które w dokładnie określonej porze dokonują obserwacji tej samej gwiazdy. Są to głównie gwiazdy o dużych gęstościach, nazywane białymi karłami.

W obrotowej kopule dachu jeden płat jest rozsuwany, umożliwiając bezpośrednią obserwację nieba.

Obserwatorium położone jest w pobliżu zielonego szlaku z Koninek przez Tobołów (z wyciągiem krzesełkowym) na Turbacz. Szlak ten prowadzi przez Polanę Suhora, z której można zobaczyć obserwatorium.

Ciekawy dla nas materiał zawarty jest w ćwiczniu dla młodych astronomów:

Oszacowanie masy supermasywnej czarnej dziury Sgr A* w centrum Drogi Mlecznej

Znajdujemy tam:

Na podstawie prawa ciążenia Newtona możemy wyprowadzić wzór na uogólnione III prawo Keplera. Mając ten wzór i znając wartości okresu obiegu jak również wielkiej półosi możemy wyliczyć sumaryczną masę ciała centralnego i ciała obiegającego. Wzór ten przedstawia się w następujący sposób:

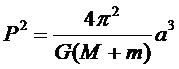
Wzór 5. Uogólnione III prawo Keplera

gdzie:
P - okres obiegu jednego ciała wokół drugiego
M - masa ciała pierwszego
m - masa ciała drugiego
a - wielka półoś orbity
G - stała grawitacji

W ćwiczeniu tym wylicza się okres przy znanych masach i znanej wielkości wielkiej półosi eleipsy. My użyjemy tej formuły dla wyliczenia wielkiej półosi elipsy. Zanim to jednak zrobimy, dostosojemy powyższą formułę do naszych potrzeb. Przy dyskusji układu podwójnego, którego jednym z elementów jest Słońce, warto posługiwać się układem jednostek, w którym odległość mierzy się w jednostkach astronomicznych, czas mierzy się w latach, masę w krotnościach masy Słońca. Wartość GM, występująca w formule nazywa się „standardowym parametrem grawitacyjnym”. Przeszukując sieć możemy znaleźć następujące informacje:

- tzw. standardowy parametr grawitacyjny ciała okrążanego (M)

The value for the Sun is called the heliocentric gravitational constant and equals 1.32712440018×10²⁰ m³s⁻².

The GM product

Main article: Standard gravitational parameter

The quantity GM — the product of the gravitational constant and the mass of a given astronomical body such as the Sun or the Earth — is known as the standard gravitational parameter and is denoted $\scriptstyle \mu\!$ . Depending on the body concerned, it may also be called the geocentric or heliocentric gravitational constant, among other names.

This quantity gives a convenient simplification of various gravity-related formulas. Also, for many celestial bodies such as the Earth and the Sun, the value of the product GM is known more accurately than each factor independently. Indeed, the limited accuracy available for G often limits the accuracy of scientific determination of such masses in the first place.

For Earth, using M_⊕ as the symbol for the mass of the Earth, we have

$\mu = GM_\oplus = ( 398 600.4418 \plusmn 0.0008 ) \ \mbox{km}^{3} \ \mbox{s}^{-2}.$

Calculations in celestial mechanics can also be carried out using the unit of solar mass rather than the standard SI unit kilogram. In this case we use the Gaussian gravitational constant which is k², where

${k = 0.01720209895 \ A^{\frac{3}{2}} \ D^{-1} \ S^{-\frac{1}{2}} } \$

and

A is the astronomical unit;

D is the mean solar day;

S is the solar mass.

^{Przyjmując, że jeden rok (sideral year) to 365.25636 dni, prowadzi to do następującej wyjątkowo prostej formuły:}

a =((1+m1)P²)^1/3

^{Uwaga: pominąłem tu czynnik 0.9999999 pojawiający się przed wyrażeniem po prawej stronie. Przyjmuję go równym 1. Fakt, że się taki czynnik, tak bliski jedności, pojawił, może sugerować, że nie jest to przypadek. Takie jednak spekulacje (że mianowicie Ziamia zajmuje tajemniczo osobliwe położenie w Układzie Słonecznym) nie będą nas interesować.}

^{Dla okresu P = 28200000 lat i masie Nemezis m1= 0.034 masy Słońca otrzymujemy orbitę o wielkiej półosi równej}

^{a = 93685.5 AU}

^{W przeliczeniu na lata świetlne (light years, l.y.) jest to}

^{a = 1.48144 l.y.}

Przypomnijmy^:

^{Najbliższa nam gwiazda poza Słońcem, to Proxima Centauri (niewidoczna gołym okiem gwiazda związana grawitacyjnie z jasną gwiazdą Alfa Centauri), odległa o 39,9 Pm (petametrów) =}^{4,22 l.y.}^{(lat świetlnych,}

^{Pozostaje nam do wyliczenia mała oś elipsy. Ale do tego potrzebna nam będzie hipoteza dotycząca peryhelionu – najbliższej odległości Nemezis od Słońca. Tym zajmiemy się w następnej notce.}