Mody normalne

W czym rozchodzą się fale? To zależy od tego co to za fale. Falują notowania giełdowe, falują ludzkie uczucia, faluje powietrze, faluje woda. Mówimy o falach wypadków drogowych i o falach przestępstw. Falują notowania polityków. Nikt z tym nie ma problemu. Uczymy się fale generować i fale tłumić. A jednak gdy przychodzi do fale elektromagnetycznych, wtedy zaczynają się dyskusje. Czy pole elektromagnetyczne potrzebuje „eteru”? Co to jest eter? Jakie ma własności? Czy wielki Albert Einstein miał rację czy nie rugując eter z fizyki?

Jest przestrzeń i mało kto w to wątpi. Są przedmioty w tej przestrzeni, przedmioty materialne, takie jak krzesła i stoły. Gdy uderzymy się o kant stołu – czujemy jego materialność dotkliwie. Ale czy tylko krzesła i stoły istnieją w przestrzeni? Co jeszcze? Długość boku stołu mogę zmierzyć metrem. Ale nie muszę mierzyć. Mam wyczucie odległości. Nawet gdy stołu w przestrzeni nie ma, mogę sobie go w niej wyobrazić i w myślach ocenić jego długość. Mogę rozejrzeć się po pokoju i ocenić odległość od od sufitu do podłogi. Ale mogę również sobie wyobrazić punkt o dwadzieścia centymetrów od sufitu i inny punkt pod nim, dwadzieścia centymetrów nad podłogą i mieć pewność, że pomiędzy tymi dwoma punktami jest określona odległość. Innymi słowy, odległość istnieje w przestrzeni. Nie potrzebujemy do tego żadnego eteru, by stwierdzić, że odległość nie jest czymś dowolnym, że podlega zbadanym prawidłowościom – na przykład prawu Pitagorasa. Wiedzieli o tym starożytni, wiedzą o tym budowniczy.

Skoro w przestrzeni może istnieć tak trudno dotykalna rzecz jak odległość, mogą w niej istnieć i inne rzeczy, równie trudno dotykalne, a jednak z określonymi prawami. Podobnie jak odległość mogą te rzeczy być mierzalne poprzez ich skutki a nie same w sobie. Czemu pole elektromagnetyczne nie miało by być jedną z takich rzeczy? Oczywiście pole elektromagnetyczne byłoby rzeczą inną od odległości, choć może nawet jakoś z nią związaną. Miast prostego prawa Pitagorasa pole elektromagnetyczne może podlegać innym, bardziej skomplikowanym prawom – na przykład równaniom Maxwella. Z równań Maxwell wynika istnienie fal elektromagnetycznych. Dzięki falom elektromagnetycznym mamy telegraf, radio, telewizję, GPS i WiFi. Przestrzeń wokół nas jest dziś wypełniona elektromagnetycznym smogiem, który z trudem i z nie do końca zbadanymi konsekwencjami znoszony jest przez nasze organizmy. Wiedza o falach zatem nie zaszkodzi, w każdym razie nie zaszkodzi bardziej niż same fale. A fale mogą być wykorzystywane zarówno dla dobra jak i na szkodę człowieka.

Cegiełką strukturalną na której wszystkie zjawiska falowe się opierają jest równanie falowe. Pisałem o num już trochę w dwóch poprzednich notkach. Nadszedł dziś czas by się temu stworzeniu przyjrzeć bliżej. Oczywiście nie mogę wchodzić w zawiłości matematyczne problemu i wyjaśniać wszystko od A do Z – od tego są podręczniki. Mogę jednak oddać smak problemu. I tak postaram się zrobić. Poruszę dziś nieco głębiej problem fal stojących i opiszę mody równania falowego lub, co na to samo wychodzi, porozmawiamy o modach drgającej struny. Bowiem wychylenia od położenia równowagi idealnej, sprężystej, naciągniętej struny spełniają równanie falowe. Przez idealną strunę rozumiem tu strunę której wychylenia spełniają właśnie równanie falowe. Takich strun w rzeczywistości nie ma. Każda rzeczywista struna, z czego by nie była zrobiona, będzie zachowywać się nico inaczej niż obiekt idealny. Ale podobnie jest z prawem Pitagorasa. Boki rzeczywistych trójkątów nigdy nie są idealnie proste ani też boki rzeczywistych ekierek nie są idealnie pod kątem prostym. Nie przeszkadza nam to jednak, a nawet gdy zaczyna przeszkadzać, znajdujemy zwykle sposoby obejścia trudności.

Przyjrzyjmy się zatem idealnej strunie i związanemu z nią równaniu falowemu. Struna zaczepiona jest na obydwu końcach, w położeniu równowagi wygląda jakoś tak:

|............................... |

Gdy jest wychylona z położenia równowagi, wtedy wygląda inaczej, np. tak

|^^^^^^^^^^^^^^|

Jedne punkty wychylone są w górę, inne w dół od położenia równowagi. (Będę tu zakładał, że struna drga tylko w jednej płaszczyźnie, góra-dół). Oznaczając przez u(x) wychylenie od położenia równowagi położenie struny w danej chwili opisane jest przez funkcję u(x).

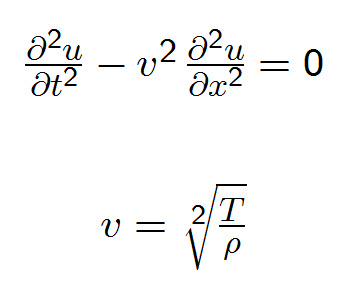
Równanie falowe

Ale z biegiem czasu położenie struny może się zmieniać. Zatem cała historia struny opisana jest funkcją u(x,t). Przypuśćmy teraz, że struna ma, w stanie równowagi napiętej, stałą długość L, że lewy koniec zaczepiony jest w punkcie o współrzędnej x=0, prawy ma x=L. Ponieważ zakładam, że lewy i prawy koniec są zaczepione na dobre, zatem nie drgają, to moge to opisać równaniami:

u(0,t)=u(L,t)=0 dla każdego t.

Uwaga: Matematycy i fizycy nazywają to warunkami brzegowymi. Ściślej, warunkami brzegowymi Dirichleta. Są także inne rodzaje warunków brzegowych, odpowiadające innym sytuacjom fizycznym – nie będziemy na razie się nimi zajmować, choć w przyszłości wrócę do tego zagadnienia.

Struna, tak zakładamy, jest idealna, zatem spełnia równanie falowe:

Matematyk powie, że jest to równanie o pochodnych cząstkowych, drugiego rzędu, liniowe i hiperboliczne. Tak powie i odeśle do odpowiedniego podręcznika. I dobrze, ale my nie chcemy być do podręcznika odsyłani, chcemy zrozumieć o co tu chodzi. Jaki z tego równania falowego i warunków brzegowych możemy odnieść pożytek? Co możemy zrozumieć? Starożytni nie znali przypuszczalnie wyższej matematyki, a jednak stworzyli całą teorię muzyki, tonów, drgań harmonicznych. My, mając do dyspozycji współczesny aparat matematyczny powinniśmy być w stanie zrozumieć to wszystko nawet głębiej, nieprawdaż? I tak jest w istocie. Współczesne programy komputerowe odtwarzające dżwięki pozwalają na dokonanie szybkiej analizy spektralnej, odszumianie, podwyższanie i obniżanie amplitudy tonów niskich i wysokich itd. A wszystko to dzięki znajomości matematyki równania falowego.

Zacznę od analizy fal stojacych. Doprowadzi nas to do pojęcia mody (innymi słowy „sposobu) drgania struny, Bowiem struna może drgać na wiele sposobów, a wśród tych nieskończenie wielu sposobów wyróznić można sposoby podstawowe, jakby atomy z których każdy inny sposób jest zbudowany. Te atomy to mody podstawowe.

Co to jest fala stojąca? Stoi – znaczy nie biegnie. Ale jak to wyrazić? Otóż matematycznie wyraża się to w ten sposób, że funkcja u(x,t) jest iloczynem dwóch funkcji, funkcji X(x) i funkcji T(t):

u(x,t)=T(t)X(x)

W każdym punkcie x amplituda zmieniają się w czasie w ten sam sposób – poprzez zależność T(t), jedynie amplituda drgania jest w różnych punktach inna.

W każdej chwili t kształt fali jest określony przez funkcję X(x), jedynie amplituda całej fali zmienia się w czasie.

Teraz przychodzi matematyczny hokus-pokus: jakie są możliwe rozwiązania równania falowego spełniające nasze warunki brzegowe a będące jednocześnie falami stojącymi? Podam odpowiedź, nie podam wyprowadzenia tej odpowiedzi. Bowiem odpowiedź jest łatwa do zrozumienia, wyprowadzenie wymaga znajomości rachunku różniczkowego i nieco teorii równań różniczkowych.

Rozwiązanie: Atomami drgań struny są drgania opisywane przez funkcje Un(x,t) dane formułą:

U_n(x,t) = cos(nΠvt/L)sin(nΠx/L)

gdzie n =0,1,2,.....

Jest więc tych atomów nieskończenie wiele, tyle ile jest liczb naturalnych. Każda inna fala stojąca jest postaci

u_n(x,t)=A_n U_n(x,t-δ_n)

gdzie A_n>0 jest amplitudą zaś delta_n – przesunięciem fazowym, czyli, innymi słowy, zmianą początku odliczania czasu.

Rozwiązania U_n(x,t) nazywamy modami normalnymi. Możemy sobie teraz te mody przedstawić.

Dla n=0 nie ma żadnych wychyleń z położenia równowagi. Struna po prostu w ogóle nie drga, u(x,t)=0 tożsamościowo, w każdym punkcie i w każdej chwili.

Dla n=1 mamy falę stojącą bez węzłów w środku struny – pierwszy stan wzbudzony:

A oto animacje tych atomów drgań kolejno dla n=1,2,3 oraz dla n=10.

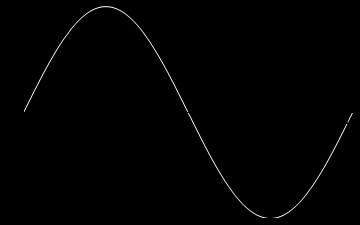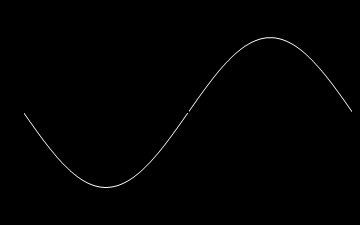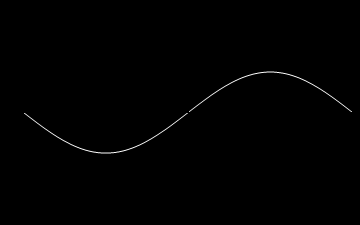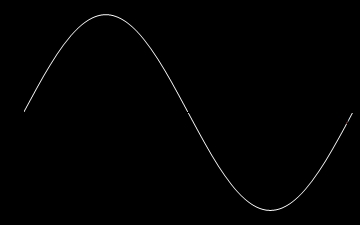
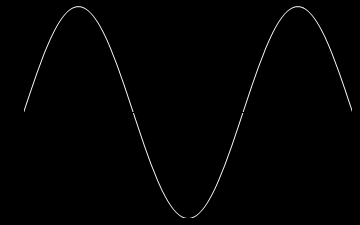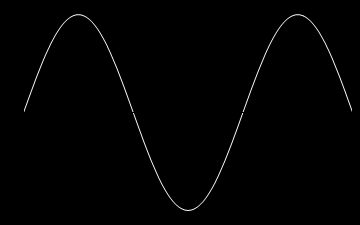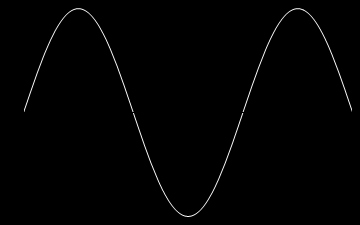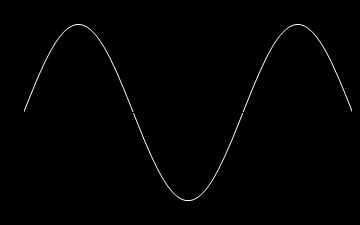
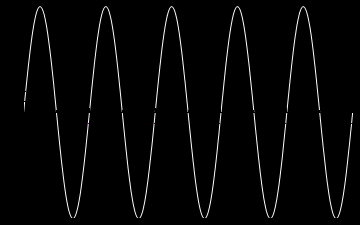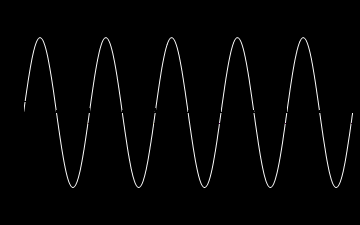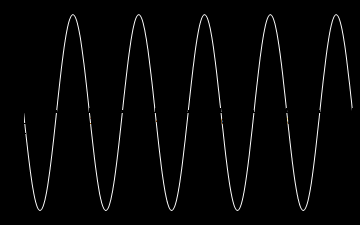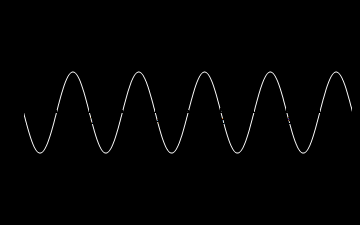
Z atomów fal możemy budować fale bardziej skomplikowane, także te biegnące. Rzecz w tym, że równanie falowe i nasze warunki brzegowe są liniowe i superpozycja fal jest dalej falą spełniającą to samo równanie i te same warunki brzegowe. Dla przykładu zbuduję falę z superpozycji atomów. Zanim jednak to zrobię jeszcze trochę o naszych atomach. Napisałem wyżej, że każda fala stojąca jest postaci:

u_n(x,t)=A_n U_n(x,t-delta_n)

Mamy to możliwe przesunięcie fazowe, które wchodzi do cosinusa. Czasem jest to wygodne a czasem nie. Znany jest wzór na cosinus różnicy katów:

cos(t-δ)=cost(t)cos(δ)+sin(t)sin(δ) = Acos(t)+Bsin(t). Wynika stąd, że możemy się pozbyć różnic fazowych jeśłi wprowadzimy drugi rodzaj atomów, mód normalnych, te drgające w fazach różniących się oΠ/2 do pierwszego. Wprowadzimy zatem atomy

V_n(x,t) = sin(npivt/L)sin(n Πx/L)

Teraz każda fala stojąca jest postaci:

u_n(x,t) = a_n cos(nΠvt/L)sin(n Πx/L)+b_n sin(nΠvt/L)sin(n Πx/L)

Nie ma tu już różnic fazowych, ale pojawiają się za to dodatkowe współczynniki b_n .

Weźmy teraz, dla przykładu, osiem atomów i następujące współczynniki a_n , b_n :dla n=1,...,8.

1, 0.607927, 0.596094

2, -0.0506606, -0.27481

3, 0.0675475, 0.180599

4, -0.0126651, -0.134778

5, 0.0243171, 0.107575

6, -0.00562895, -0.0895348

7, 0.0124067, 0.0766867

8, -0.00316629, -0.0670683

fala biegnąca

Widać na animacji jak fala biegnie po strunie. Ale końce struny są nieruchome – tak jak tego chcieliśmy. Widać, że już ośmiu atomów – zwanych czasem modami normalnymi - można zbudować prawdziwe dziwolągi!

Dla n=1 mamy modę podstawową. Jej okres drgań wynosi 2L/v. Czym dłuższa struna, tym dłuższy jest okres. Współczynnik v zależy od materiału struny i od jej napięcia. Strojąc gitarę zmieniamy właśnie v dla każdej struny. Oczywiście L dla każdej ze strun gitary jest inne. Długość strun i ich napięcia są dobierane tak, by mody podstawowe każdej ze strun harmonizowały jedna z drugą. Ale sztuka harmonii to już inna para kaloszy - nie na moje nogi.