Orbita próbnika Cassini wokół Jowisza (2004-2017)
Wiele pięknych, fundamentalnych osiągnięć fizyki i astronomii, jak i po prostu ciekawych wyników, da się udowodnić w miarę prosto (najprościej jak można, ale nie prościej, jak mawiał Albert Einstein). Dzisiaj udowodnię tak, że w problemie grawitacyjnym dwóch ciał orbity są krzywymi stożkowymi i wyprowadzę trzy empiryczne prawa Keplera opisujące ruch planet. Słynny dowód tego przeprowadził ponad 330 lat temu Izaak Newton, ale nieco inaczej, niż teraz to wyjaśniamy studentom, bo poprzez geometrię. Obecnie kładziemy większy nacisk na tzw. całki pierwsze (zasady zachowania) redukujące liczbę zmiennych. Bez zrozumienia orbit newtonowskich nie mielibyśmy czego szukać w kosmosie, nie rozumielibyśmy zachowania orbit bardziej skomplikowanych.
ZADANIE Z GWIAZDKĄ
Kopernik brawurowo rozwiązał problem miejsca Ziemi we wszechświecie, Kepler opisał doskonale orbity i kinematykę ruchu planet (zob. ten blog kierdela). Ale brakowało zrozumienia dynamiki planet, odpowiedzi na pytanie: dlaczego elipsy? Galileusz nie pomógł, nie popchnął zrozumienia dynamiki kosmosu, mimo że to on stworzył podstawy dynamiki i jego imieniem a nie Newtona powinniśmy nazywać 1sze prawo dynamiki. W roku śmierci Galileusza (wg kal. gregor. używanego wtedy w Anglii było Boże Narodzenie 1642 r.), urodził się we wsi Woolsthorpe w Anglii geniusz, który dokonał rzeczy dla innych nieosiągalnej. Nie mówię tu o tym, że rozumiał rachunek różniczkowy :-). Udowodnił matematycznie równoważność praw Keplera (pierwsze o eliptyczności orbit, drugie o stałej prędkości polowej, a trzecie o tym, że kwadrat okresu obiegu słońca proporcjonalny jest do sześcianu rozmiaru orbity) z prawem ciążenia powszechnego (siła między każdą parą ciał jest proporcjonalna do iloczynu ich mas, a odwrotnie proporcjonalna do kwadratu odległości).
NEWTON i jego ZNAJOMI
Choć historia z jabłkiem Newtona jest legendą, to na większość swych odkryć fizycznych Izaak wpadł w latach 1665-1666 w czasach gdy uniwersytet w Cambridge objęto kwarantanną ze względu na szerzącą się zarazę - wyjechał do Woolsthorpe, gdzie w ogrodzie stała słynna jabłoń. Tworzył dowody geometryczne. Ściślej, najchętniej nie dawałby żadnych dowodów, gdyż nie lubił publikować, co doprowadziło do kilku głośnych sporów o pierwszeństwo odkryć.

Do publikacji zasad dynamiki i rozwiązania matematycznego problemu dwóch grawitujących ciał w dziele Philosophiae Naturalis Principia Mathematica (1667= MDCLXXXVII) doszło w wyniku barwnej historii z udziałem fizyka Roberta Hooke'a i astronoma Edmunda Halleya. To astronom namówił do publikacji i wyłożył własne pieniądze na wydanie dzieła Newtona, gdyż ten, mimo pewnej zamożności, uznał, że jeśli publikacji nie opłaci Royal Society, to on nie poniesie kosztów i mówi się trudno...nie będzie traktatu.
Pomiędzy Hookiem a Newtonem iskrzyło. Wymieniali listy, z początku wszystko było ok. Hooke dawał Newtonowi pewne idee i motywację, które Izaak z początku doceniał. Na przykład to Hooke pierwszy wyznaczał orbity graficznie, łącząc koncepcje inercji i grawitacji, krok po kroku, podobnie jak dziś robimy to na komputerze:
 Sir Izaak użył tej konstrukcji w swym dziele, pokazując czysto geometrycznie, że z centralności siły zawsze skierowanej do źródła grawitacji S, wynika drugie prawo Keplera. Na tym rysunku (zob. też ilustracje do notki), Newton zakładając przybliżenie impulsowe, tzn. że siła przykładana jest bardzo krótko w punktach B, C, D, E, itd., stosując geometrię z 8 kl. szkoły podstawowej, mianowicie twierdzenie, że trójkąty o jednym takim samym boku i prostopadłej do niego wysokości mają te same pola, udowodnił iż pola ASB, BSC, CSD itd. są sobie równe. (Najpierw pokazał że pole ASB = BSc, a potem, że to z kolei jest również polu BSC. Punkt c osiągnięty byłby bez działania siły. Zachęcam do przekonania się patrząc na rysunek, że miał rację. Wektor cC = BV to chwilowa zmiana prędkości w punkcie B, w kierunku BS, razy krok czasowy). Na koniec Newton przeszedł do granicy nieskończenie krótkich kroków czasowych i udowodnił, że pole zakreślane przez wektor wodzący rośnie liniowo w czasie.
Sir Izaak użył tej konstrukcji w swym dziele, pokazując czysto geometrycznie, że z centralności siły zawsze skierowanej do źródła grawitacji S, wynika drugie prawo Keplera. Na tym rysunku (zob. też ilustracje do notki), Newton zakładając przybliżenie impulsowe, tzn. że siła przykładana jest bardzo krótko w punktach B, C, D, E, itd., stosując geometrię z 8 kl. szkoły podstawowej, mianowicie twierdzenie, że trójkąty o jednym takim samym boku i prostopadłej do niego wysokości mają te same pola, udowodnił iż pola ASB, BSC, CSD itd. są sobie równe. (Najpierw pokazał że pole ASB = BSc, a potem, że to z kolei jest również polu BSC. Punkt c osiągnięty byłby bez działania siły. Zachęcam do przekonania się patrząc na rysunek, że miał rację. Wektor cC = BV to chwilowa zmiana prędkości w punkcie B, w kierunku BS, razy krok czasowy). Na koniec Newton przeszedł do granicy nieskończenie krótkich kroków czasowych i udowodnił, że pole zakreślane przez wektor wodzący rośnie liniowo w czasie.
Hooke został jednak w końcu arcywrogiem Newtona (o to nie było trudno; geniusz miał trudności w kontaktach międzyludzkich i nie tolerował konkurencji, a Hooke też potrafił hejtować, nawet raz publicznie ośmieszył szkice trajektorii zrobione przez Newtona). Hooke miał doskonałe pojęcie o grawitacji powszechnej, nawet przed Newtonem opisał prawo ciążenia wraz z jego odwrotną proporcjonalnością do kwadratu odległości w małej książce, na nowo odkrytej w przepastnych archiwach zamykanej pod koniec ub. wieku biblioteki Obserwatorium Greenwich. Tam stwierdził, że ostateczny dowód, iż wykładnik jest równy dokładnie 2, to domena eksperymentu. Jak to zresztą zawsze jest w fizyce: teoria teorią, ale musi być poparta eksperymentem. Hooke był genialnym intuicjonistą i eksperymentatorem, ale nie potrafił dać matematycznego dowodu, że z praw Keplera wynika ściśle, że siła przyciągania jest odwrotnie proporcjonalna do kwadratu odległości, i odwrotnie.
O taki dowód prosili uczestnicy dyskusji odbywających się po spotkaniach Królewskiego Towarzystwa Naukowego w londyńskiej kawiarni naukowcy: Halley, architekt i astronom Christopher Wren i inni. Halley wyznaczył nawet nagrodę pieniężną w 1684 r. Hooke powiedział, że tak, potrafi to udowodnić i pokaże dowód następnym razem. Nie pokazał. Halley pojechał wtedy do Cambridge do Newtona, porozmawiać o dowodzie. Newton powiedział, że tak, udowodnił to cztery lata wcześniej, nie mógł jednak w bałaganie odnaleźć notatek i obiecał je przesłać później (a więc znów "następnym razem"). Halley czekał i czekał, aż zwątpił i w Newtona. Ku radości astronoma, fizyk w końcu jednak dotrzymał słowa. Po kilkunastu miesiącach obsesyjnej pracy, kiedy Newton często zapominał o posiłkach, manuskrypt był gotów. "Zasady Matematyczne Filozofii Przyrody" są uznane obecnie za najważniejszą książkę o fizyce w całych jej dziejach.
ORBITY DWÓCH CIAŁ - DZISIAJ
Jak większość twierdzeń matematyczno-fizycznych, jest wiele dowodów na związek grawitacji Hooka... tj. Newtona, z orbitami opisanymi tak dobrze przez Keplera. Obecnie dajemy studentom wyższych lat studiów następujący dowód, w istocie cały wykład, sam w sobie pokazujący też piękno prostych działów matematyki, takich jak analiza wektorowa. Nie jest to dowód ani czysto geometryczny jak w Principiach, ani nie wymaga znajomości rachunku całkowego (głównie takie ujęcie stosowano w pedagogice kiedyś). Jest ścisły, prosty, nowoczesny. Oparty jest o poszukiwanie całek pierwszych równania, wielkości stałych w czasie, każda z których eliminuje jedną zmienną w równaniu. To udaje się w przypadku tzw. całkowalnych hamiltonowskich układów dynamicznych, jakim jest niewielki układ dwóch ciał poruszających się bez oporu, w próżni. Wymagane wiadomości wstępne to wzór na siłę grawitacji i umiejętność liczenia pochodnych. Ten odcinek bloga nie ma ani jednego odsyłacza, gdyż wszystkie potrzebne zasady zachowania i wszystkie wyniki wyprowadzamy tu na kilku stronach.
Czy 2 = 1 ?
Sformułujmy i zredukujmy najpierw problem 2 ciał do problemu 1 ciała. Jak to możliwe? Położenie i prędkość (czy pęd) każdego ciała opisuje 6 zmiennych, 3 składowe położenia i 3 prędkości. Jednak łatwo wyczuć, że połowa wszystkich zmiennych (6) tak naprawdę opisuje jednostajny i prostoliniowy ruch środka masy układu dwóch ciał, zgodnie z zasadą inercji Galileusza (nasze dwa ciała nie są poddane żadnym siłom zewnętrznym). Pozostałe zmienne będą opisywać ruch jednego ciała względem drugiego, czyli orbitę względną. Ponieważ na forum niełatwo jest odtworzyć symbole wprowadzone przez Newtona takie jak kropki nad zmiennymi (w tym wektorami), oznaczające pochodną po czasie czyli szybkość zmian w czasie, to posłużę się bazgrołami odręcznymi, gdzieniegdzie opisanymi na cześć Sir Izaaka po angielsku.
Opowieść rozpoczynają wektorowe równania ruchu dwóch ciał, opisywanych indeksami 1 i 2. Wektory oznaczam pogrubieniem. Wolno myśleć o ciele 2 jako mniej masywnym, ale nie jest to konieczne. Po lewej mamy siły jako iloczyny mas i wektorów przyspieszenia, czyli drugich pochodnych położeń r1,2 , natomiast po prawej stronie wyrażenia na siły przyciągania, podające nie tylko wartość siły (Gm1m2/r2), ale także jej zwrot wzdłuż odpowiedniego wektora jednostkowego r/r. Siła grawitacji działa wzdłuż wektora r =r2 - r1. Niech was nie myli sześcian odległości we wzorach, to naprawdę kwadrat, ale dorzucono tam jeszcze jedną potęgę, dzielnik z wersora r/r (niepogrubione r = |r|).
Najpierw dodajemy dwa równania wektorowe ruchu stronami. Prawe strony sumują się do zera, ponieważ suma sił działających na dwa ciała jest zerowa (siły i przyspieszenia ciał są równe co do wartości i przeciwnie skierowane, zgodnie zresztą z 3. zasadą dynamiki Newtona). Lewe strony, zsumowane, dają sumę pierwszych pochodnych czasowych pędów. Innymi słowy, całkowity pęd nie zmienia się w czasie (zasada zachowania pędu). Definiując kombinację wektorów wodzących dwóch ciał ważoną ich masami jako wektor środka masy układu: rCM = (m1 r1 + m2 r2)/(m1 + m2), widzimy, że środek masy porusza się jednostajnie, bez przyspieszenia. (Bez utraty ogólności możemy więc umówić się, że jesteśmy w układzie inercjalnym środka masy, gdzie rCM = 0, jeśli tego nie zrobimy to mała różnica, ale będziemy musieli pamiętać o dodaniu jednostajnego ruchu środka masy do rozwiązania).

Odejmując stronami równania wektorowe ruchu dwóch ciał podzielone przez masy tych ciał, otrzymujemy równanie orbity względnej (ostatnie w powyższym arkuszu, a w zielonej ramce poniżej). To nasze zasadnicze równanie do rozwiązania. Jak widać, równie dobrze mogłoby opisywać ruch jednej cząstki próbnej w ustalonym polu siły grawitacji, pochodzącej od ciała, którego masa jest arytmetyczną sumą mas dwóch rozpatrywanych ciał (M = m1+m2). Dokonaliśmy redukcji zagadnienia 2 ciał do zagadnienia 1 ciała. Jeśli bowiem rozwiążemy równanie na r(t), czyli na ruch ciała 2 względem ciała 1, to będziemy mogli bardzo prosto odtworzyć rozwiązania na ruch ciała 1 i 2 w układzie inercjalnym, przeskalowując rozwiązanie r(t), jak widać u góry następnej strony notatek.
Idźmy dalej. Weźmy teraz iloczyn wektorowy r i obu stron równania ruchu względnego. Iloczyn wektorowy znika, jeśli mnożone wektory są współliniowe, co jest prawdą po prawej stronie naszego równania w zielonej ramce. Dlatego i lewa strona, iloczyn wektorowy wektora r i jego drugiej pochodnej (przyspieszenia) jest zerem. Ale ta lewa strona to nic innego jak pochodna czasowa momentu pędu! A ściślej, właściwego momentu pędu (ang. specific angular momentum), czyli momentu pędu pozbawionego stałej będącej masą. W fizyce pełnym momentem pędu nazywamy masę razy iloczyn wektorowy położenia i prędkości, czyli inaczej iloczyn wektorowy położenia i pędu. W astrofizyce bardzo często mamy do czynienia z badaniem ruchu ciała próbnego o tak małej masie, że nie warto wszędzie wpisywać tej masy, bo i tak się w końcu skróci. Lepiej mówić trochę nonszalancko o pędzie i momencie pędu, podczas gdy zapisujemy w istocie te wielkości podzielone przez masę ciała próbnego. Trajektoria w układzie słonecznym satelity o masie 1 tony i mikrosatelity o masie 1 kg nie różnią się praktycznie, po co nam zatem pisać we wszystkich równaniach te mało ważne masy. Otrzymaliśmy zasadę zachowania momentu pędu L. (będę pisał tu L zamiast l, bo l trudno w ogóle w tekście drukowanym odróżnić od jedynki; odręczne małe "L" jest dużo łatwiej rozpoznać).
L = r x v = const.
Z niej wynika i drugie prawo Keplera i to, że orbita w zagadnieniu dwóch ciał jest dwuwymiarowa, płaska:

W powyższym, A(t) oznacza pole zakreślane przez wektor r orbitującego ciała. Podana jest interpretacja geometryczna zasady zachowania momentu pędu: to prawo stałej prędkości polowej Keplera (drugie prawo Keplera). Planeta lub kometa poruszająca się koło Słońca, np. po elipsie, omiata wektorem r(t) równe pola w równych odstępach czasu, wszystko jedno czy jest daleko czy blisko gwiazdy.
Wektor r można opisać w biegunowym układzie współrzędnych: długość wektora to r(t), a kąt w stosunku do osi układu to θ(t), podobnie wektor prędkości można rozłożyć na składowe radialną i poprzeczną. Fajne jest to, że całe zagadnienie redukujemy nie tylko z 6 do 3 zmiennych, ale dalej aż do poszukiwania tylko 1 zmiennej. Oto dlaczego. Płaszczyzna ruchu musi być niezmienna, ciała nie mogą jej opuścić, ponieważ (stały) wektor L jest zawsze prostopadły do wektora r. Iloczyn skalarny r i L równy jest zeru, gdyż L = r x v jest prostopadły do r, a iloczyn skalarny wektorów prostopadłych znika. Czyli płaszczyzna ruchu jest prostopadła do L. Zamiast trzech zmiennych przestrzennych, np.x(t), y(t), i z(t), pozostają już do wyznaczenia tylko dwie (r, θ). Przy tym prędkość poprzeczna vθ(t) = r(t) dθ/dt pomnożona przez r(t) daje L = |L|, wielkość stałą. Stąd, gdy już wyznaczymy osobno rozwiązanie na r(t), będziemy mogli powrócić do θ(t), i znaleźć tę funkcję całkując równanie różniczkowe dθ/dt = L/r2(t) po czasie: θ(t) = L ∫ r-2(t) dt. Zadanie sprowadza się więc do rozwiązania zagadnienia jednowymiarowego, radialnego.
Idźmy dalej, jesteśmy bowiem o krok od udowodnienia zasady zachowania energii. Ruch radialny opisać można dokonując operacji iloczynu skalarnego z wektorem prędkości, po obu stronach równania ruchu względnego (tego w zielonej ramce):

Lewa strona otrzymanego równania (skalarnego) to po prostu pochodna po czasie energii kinetycznej na jednostkę masy (v2/2), jak widać powyżej. Prawa strona to -1 razy pochodna czasowa potencjału (-GM/r), co sprawdzamy różniczkując funkcję (-1/r): d(-1/r)/dt = (1/r2) dr/dt, gdzie dr/dt = d (x2 + y2 + z2)1/2/dt = [x dx/dt + y dy/dt + z dz/dt]/r. Oznaczając gwiazdką iloczyn skalarny: -d(-GM/r)/dt = -(GM/r3) r * v = prawa strona równania, co chcieliśmy pokazać. Energia całkowita E = suma energii kinetycznej i potencjalnej, jest stała. (W odręcznym tekście to samo zostało udowodnione inaczej, wprowadzając pojęcie potencjału siły i pochodnej adwektywnej, tak aby nawiązać do innych działów fizyki - nie jest to konieczne).
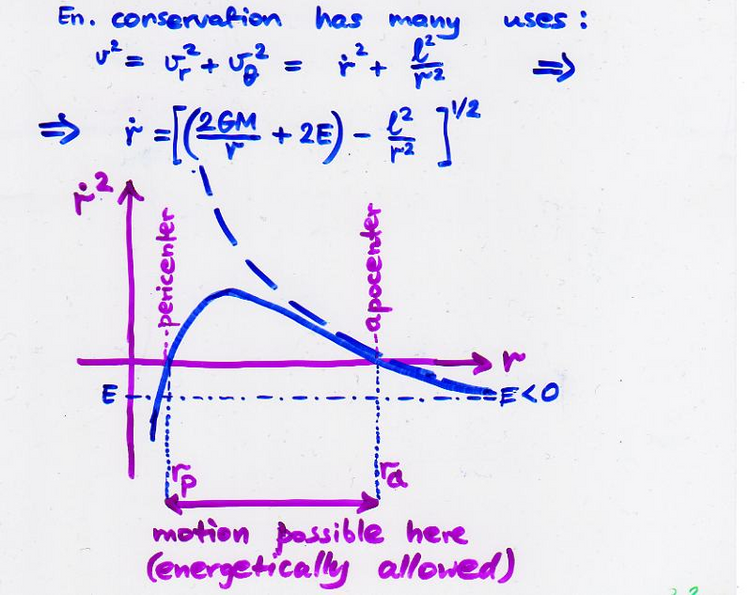
To wykorzystać możemy do udowodnienia, że w ruchu o niezerowym L i ujemnej energii całkowitej E<0, gdzie dwa ciała są związane permanentny w układ podwójny, niezdolne uciec do nieskończoności, istnieje nie tylko maksymalna ich odległość zwana odległością apocentrum (aphelium, apogeum, ..) ale także minimalna, prycentrum (peryhelion, perygeum, ...). Te odległości, rp,a, łatwo obliczyć z zasady zachowania energii.
Zasadę zachowania energii możemy też użyć do wyznaczenia nieznanej prędkości radialnej dr/dt, jak widać eksplicite na powyższym rysunku. Dla ustalonych, stałych L i E, prędkość radialna jest znaną funkcją promienia r, jest to więc skomplikowane równanie różniczkowe na r(t) w postaci dr/dt = f(r), które rozwiązać można będąc bardzo sprawnym w całkowaniu, najpierw rozdzielając zmienne i całkując: ∫ dr/f(r) = ∫ dt = t + const., a następnie (co nie jest trywialne!) z zależności t = t(r) wyłuskując szukaną zależność r(t). Na końcu, jak mówiliśmy, przecałkować trzeba jeszcze funkcję r-2(t) po czasie by dostać θ(t). Hmm..
Jest szybsza i jak mi się wydaje dużo bardziej elegancka droga, by udowodnić że orbity są krzywymi stożkowymi: elipsą, parabolą lub hiperbolą.

 Pierre-Simon, Marquis de Laplace (1749-1827)
Pierre-Simon, Marquis de Laplace (1749-1827)
Przyjrzyjmy się co tu się dzieje w powyższych bazgrołach. Wyrażenie definiujące wektor momentu pędu przemnożyliśmy obustronnie przez wektor przyspieszenia. Lewa strona to pochodna po czasie v x L. Prawą stronę też chcielibyśmy przekształcić do postaci pochodnej czasowej czegoś. Wówczas, jak w przy wyprowadzaniu zasad zachowania momentu pędu i energii pewne "coś" będzie stałe w czasie, tu oczywiście będzie to wektor L-R-L. Okazuje się że prawa strona to w zasadzie pochodna czasowa wersora r/r, stąd dwuskładnikowa postać wektora e, z udziałem tego wersora.
Trajektorie
Następnie badamy własności wektora e. Pierwszą jest prostopadłość do L. Iloczyn skalarny e i L jest równy zeru, czyli r i e leżą zawsze w tej samej płaszczyźnie prostopadłej do stałego momentu pędu: w płaszczyźnie orbity. Oznaczmy kąt pomiędzy nimi jako θ. Nazywamy go w astronomii anomalią prawdziwą. Drugą ciekawą własnością jest wartość iloczynu skalarnego e i r, to znaczy: e r cos(θ). Po nieskomplikowanych obliczeniach, wartość ta okazuje się być równa L2/GM - r, skąd otrzymujemy równanie
r (1 + e cosθ ) = L2/(GM) = const.
I tak właśnie, proszę Państwa, udowodniliśmy uogólnione pierwsze prawo Keplera, które zwykle spotykamy w formie, gdzie stałą L zastępujemy nową stałą a, defniując ją jako L2 /(GM) =: a (1-e2)
r = a (1-e2) / (1 + e cosθ).
Jest to matematyczne równanie elipsy w układzie biegunowym. (Nasze pierwsze równanie opisuje także inne krzywe: parabole, hiperbole). Stała a jest półosią dłuższą elipsy (połówką dłuższej osi), zaś e to mimośród (u nas to po prostu e=|e|, długość wektora Laplace'a). Kątowi θ=0, odpowiada punkt najbliższy, perycentrum trajektorii. Wektor Laplace'a skierowany jest od ciała centralnego do perycentrum.
To bardzo wygodne. W zagadnieniu 2 ciał, e jest wektorem stałym, ale pod wpływem zaburzeń od ciał trzecich będzie gdzieś wędrował i zmienial długość, orbita może zmieniać i rozmiar i stopień spłaszczenia. Śledząc ewolucję kierunku e, poznamy ruch precesyjny orbity w przestrzeni, a zmiany długości e poinformują o zmianach kształtu elipsy. Na ogół takie zmiany są bardzo powolne. Ani kształt ani płożenie orbity nie są zauważalnie inne po jednym okresie orbitalnym. Możemy opisać faktyczne tory ruchu w układach planetarnych jako wolno ewoluujące elipsy. Elipsę chwilowo opisującą ruch ciała nazywamy oskulującą. Oprócz zasadniczych dla astrofizyki elementów: a, e, i (nachylenie płaszczyzny orbity do jakiejś ustalonej płaszczyzny układu współrzędnych), są też dwa inne. Jeden (ω) to długość perycentrum, drugi to długość węzła wstępującego orbity (Ω). Te kąty ("długości" jak "długość geograficzna") są potrzebne by zorientować odpowiednio orbitę w jakimś układzie współrzędnych. Ostatnim z 6 elementów orbitalnych jest czas dowolnego przejścia przez perycentrum.
Poniższa tabela przedstawia znaną dobrze interpretację krytycznych wartości e=0 i e=1, dających podział na tory kołowe, eliptyczne, paraboliczne i hiperboliczne, i odpowiadające im znaki energii E. Wyprowadzony jest też ważny związek energii E i największej średnicy orbity 2a: E = -GM/(2a). Energia orbity nie zależy od mimośrodu e, zależy tylko od półosi wielkiej. Inaczej jest z momentem pędu: L2 = GMa(1-e2). Ten zależy i od a i od e. Wśród orbit ustalonym momencie pędu orbita kołowa (e=0) ma najmniejszą półoś a. I tak dalej... Wsród ilustracji umieściłem szkic czterech orbit o tej samej osi wielkiej, mają więc tę samą orbitalną energię mechaniczną, ale różny moment pędu, im mniejszy tym bardziej wydłużona elipsa.

Do udowodnienia pozostało trzecie prawo Keplera:
Dowód dla orbit eliptycznych, w tym kołowych, opiera się na drugim prawie Keplera. Okres orbitalny nazwiemy P. Mamy z drugiego prawa dA/dt = const., gdzie dA = pole pow. zakreślane w czasie dt. W ciągu czasu P zakreślana jest cała elipsa:
Prędkość polowa * P = Pole elipsy = π a b
a = półoś wielka elipsy, b = półoś mniejsza elipsy; w elipsie mamy też jak mówiliśmy już: (b/a)2 = 1–e2 .
Zatem P = 2π a b / L, albo biorąc pod uwagę L = [GMa(1-e2)]1/2, inaczej:
P = 2π (GM)-1/2 a3/2 (3cie uogólnione prawo Keplera)
Średnią prędkość kątową ciała na orbicie eliptycznej (tzw. ruch średni) wyznaczmy dzieląc kąt pełny przez okres orbitalny: n = 2π/P = (GM/a3)1/2.
To wszystko! Piękne z pożytecznym.... Wyprowadzone relacje mają bardzo wiele zastosowań w astronautyce, astronomii i astrofizyce. Trzecie prawo Keplera mówi np. jak długo czerwony samochód Tesla3 pana Muska musi lecieć na Marsa. Co ważniejsze, uogólnienie do powyższej postaci, w której masa M nie jest koniecznie masą Słońca, w połączeniu z obserwacjami okresów orbitalnych i rozmiarów orbit, pozwoliło 'zważyć' gwiazdy, galaktyki i bardziej egzotyczne obiekty kosmiczne. Okresy obiegu gwiazd w samym centrum naszej Galaktyki dały masę czarnej dziury tam leżącej (ponad 3 miliony mas słonecznych).
Nie wspomniałem tylko o tym, jak wyznaczmy efemerydy, chwilowe położenia i prędkości ciała na orbicie, w zadanym momencie czasu, ze znanych elementów orbity. Trzeba w tym celu ułożyć i rozwiązać (jest ponad sto opublikowanych sposobów rozwiązywania) tzw. równanie Keplera. Nie ma prostych rozwiązań analitycznych w funkcjach elementarnych. Myśląc o nim, matematycy rozwinęli kiedyś parę nowych działów matematyki.
















Komentarze
Pokaż komentarze (59)