Administratorów proszę o zakwalifikowanie notki do działu "Katastrofa Smoleńska", gdyż dotyczy to dyskusji tam prowadzonej.
Spróbujmy wykonać eksperyment, który wykaże jakie jest to nieszczęsne przeciążenie przy schodzeniu ze schodów. Nagrałem taki oto filmik:
Na tym filmie zbiegałem (ale nie z maksymalną prędkością - taki truchcik powiedzmy) na gołych stopach ze schodów. Film nagrany jest w 50 fps, a więc jedna klatka to 0,02 sekundy.
Najpierw policzmy prędkość stopy. Na filmiku potrzeba 4 klatek aby stopa dotknęła ziemi. Weźmy nawet 5, bo może kawałek z tych 20 cm jest poza kadrem. Prędkość stopy przy lekkim zbieganiu ze schodów (20 cm w 5 klatek tj. 0,1 sekundy):
v=s/t=2 m/s
Teraz policzmy przyspieszenie działające na przednią część stopy. Według mnie wyhamowanie tej prędkości odbywa się na przestrzeni maksimum jednej klatki (być może i mniej ale za wolną mam kamerę). W związku z tym przyspieszenie działające na przednią część stopy (2 m/s w czasie 0,02 sekundy)
a=v/t=100 m/s^2 ~ 10g (i to jest dolne oszacowanie)
Takiego przeciążenia doznaje przód stopy.
Spróbujmy teraz oszacować przeciążenia, które można by zmierzyć na pięcie. Jak widać część prędkości wyhamowuje ona wraz z przednią częścią stopy ale trochę jej zostaje - potrzebuje jeszcze 4 klatek na dotknięcie ziemi na zmierzonym dystansie ok. 10 cm. Czyli jej średnia prędkość, po dotknięciu stopą ziemi (10 cm w 0,08 sekundy)
v=s/t=1,25 m/s
Wyraźnie widać, że nie jest to prędkość stała - pięta zwalnia. Dlatego szacunkowo w górnej części może mieć ok 1,5 m/s a w dolnej ok 1 m/s.
Ponieważ oba procesy znów dzieją się za szybko, przyjmując minimalny mierzalny interwał czasowy t=0,02s wychodziłoby hamowanie w górnej części
a=25 m/s^2 ~ 2,5g
I w dolnej:
a=50 m/s^2 ~5g
Mierząc więc na pięcie (albo na kostce etc.) spodziewałbym się dwóch peaków -ok. 2,5g i ok 5g a pomiędzy nimi względnie stałego przyspieszenia. Przyspieszenie to też można oszacować (4 klaty i utrata ok. 0,5 m/s z prędkości)
a=2s/t^2=16 m/s^2 ~1,5g
Spodziewałbym się więc mniej więcej takiego pomiaru przyspieszeń:
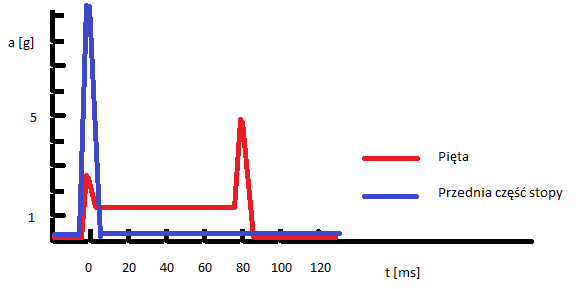
Wykres jest bardzo schematyczny. W rzeczywistości pola pod krzywymi powinny być takie same.
Oczywiście to co się dzieje wyżej, będzie coraz lepiej amortyzowane. Na piszczelu będzie mniej a w środku ciężkości jeszcze mniej i powinno to zmierzać tam do określonych wartości reakcji podłoża.
Należy też pamiętać, że to są szacowane przyspieszenia, a nie przeciążenia. Aby uzyskać te drugie trzeba jeszcze dodać ziemskie 1g. Oczywiście nie wykluczam też, że w tym rozumowaniu tkwi jakiś błąd, choć wydaje mi się, że to dość elementarne rachunki.








Komentarze
Pokaż komentarze (189)