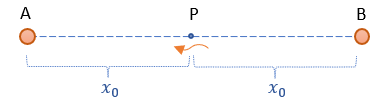
U podstaw Teorii Względności leży elementarne pytanie odnoszące się do poniższego rysunku:
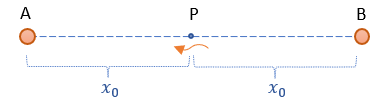
Co się dzieje z punktem przestrzeni P jeśli obiekty A i B oddalają się od siebie z prędkością v? Możemy przyjąć dla naszych dydaktycznych celów, że w całym wszechświecie są tylko te dwa obiekty i przestrzeń. Kto umie odpowiedzieć na zadane pytanie?
Punkt przestrzeni nie ma masy, to tylko fizyczne miejsce w tejże przestrzeni. Żeby nie był on taki całkiem abstrakcyjny, niech to będzie miejsce w którym akurat znajduje się foton lecący w kierunku obiektu A.
Okazuje się, że odpowiedzi dostarczył Lorentz za pomocą swojej Transformacji. A mówiąc precyzyjnie założył (przecież tego punktu nie widać), że punkt P jest nieruchomy względem każdego obiektu A i B. Problem oczywiście w tym, że te obiekty się oddalają i tu z pomocą przychodzi układ odniesienia. Punkt P jest nieruchomy względem każdego obiektu ale tylko w jego własnym układzie odniesienia.
Lubię jak najprostsze modele (ale nie prostsze, jak mówił Einstein:-) i można tę przestrzeń Lorentza (Hendrika, nie George’a) porównać do dwóch patyczków przyczepionych odpowiednio do obiektów.

Po oddaleniu się obiektów A i B, punkt P niezmiennie zajmuje początkowe miejsce na patyczku, czyli w swoim układzie odniesienia. Widzimy to na kolejnym rysunku, gdzie obiekty oddaliły się o odległość Δx, a foton w tym czasie zdążył już dolecieć do obiektu A.
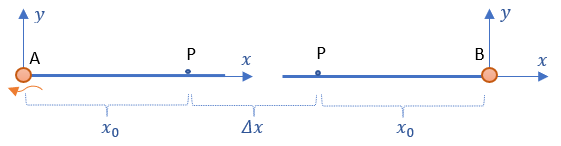
No i teraz chodzi o to, żeby znaleźć jakąś formułę matematyczną, która taki model ruchu pozwoli opisać w jednakowy sposób dla każdego układu odniesienia.
Na pierwszy rzut oka to „kwadratura koła”, bo co powiemy o prędkościach wyliczonych w każdym układzie?
W układzie A prędkość oddalania się obiektów v możemy wyliczyć z następującego wzoru.
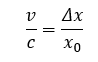
Ale już w układzie B ta sama prędkość ma inną wartość.
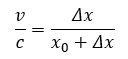
A przecież nie może być tak, że prędkość oddalania się A od B jest inna, niż prędkość oddalania się B od A. Prędkość ma być niezmiennikiem w tym przekształceniu. Czy coś można tu zrobić, żeby zapewnić zgodność obu równań? Jaki sposób znalazł na to sam Lorentz?
Skoro nie możemy zmienić prędkości, to musimy skorygować odległość – nie ma innej możliwości, żeby powyższe rachunki się zgodziły.
Rozpiszmy zatem Δx jako Δx =xB - xA. Gdzie xA=x0 jest drogą fotonu w układzie A. Natomiast xB jest drogą fotonu w układzie B.
Na czym będzie polegała korekta? Wszelkie odległości mierzone w układzie własnym zostawimy niezmienne, ale każdą odległość w „obcym” układzie przeskalujemy dzieląc przez jakiś współczynnik γ. A zatem prędkość w układzie A przybierze poniższą postać.
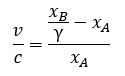
Natomiast prędkość w układzie B po rozpisaniu będzie miała analogiczny kształt.
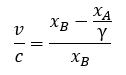
No to wyliczmy γ, czyli wartość tej korekty niezbędnej do uzyskania zgodnych wyników. Przekształcając powyższe wzory otrzymamy:
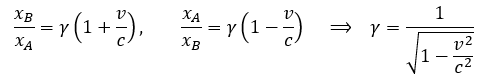
Archimedes pewnie krzyknąłby Eureka. Może to samo zrobił Lorentz podstawiając otrzymany współczynnik do obu równań i uzyskując swoją słynną transformację.
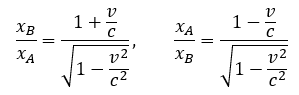
Zauważmy, że drugi wzór jest po prostu przekształceniem pierwszego. A zatem otrzymaliśmy jedną wspólną formułę ruchu dla obu układów. A skoro jest to ten sam wzór, to zajmijmy się pierwszym. Kolejne przekształcenia pozwalają zapisać wyprowadzoną właśnie Transformację Lorentza w powszechnie znanej postaci.
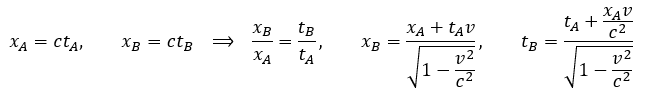
Mam nadzieję, że za pomocą przedstawionego wyprowadzenia udało się pokazać Transformację Lorentza „od kuchni”. Jak widać nie ma tu magii, a dokonana korekta w swoisty sposób zaginająca geometrię wynika po prostu z niezbędnej konieczności dostosowania obliczeń do przyjętych założeń.
„Do przyjętych założeń” – słowo klucz. Przypomnijmy w takim razie te założenia. Przyjęliśmy, że punkt przestrzeni jest nieruchomy względem każdego układu odniesienia. Nasuwa się pytanie, czy otrzymalibyśmy inne wzory opisujące naszą rzeczywistość, gdybyśmy na początku przyjęli inne założenia. Spójrzmy na początkowy rysunek raz jeszcze.
Czy widzimy jakiś inny możliwy sposób zachowania się punktu P, niż jednoczesna obecność na dwóch „patyczkach” rozsuwanych razem z obiektami A i B?
Sprawdźmy najprostszy pomysł, który się narzuca. Załóżmy, że punkt P podczas oddalania obiektów A i B pozostaje w swoim centralnym położeniu między nimi. Wtedy sytuacja po dotarciu fotonu do obiektu A będzie przedstawiała się tak:
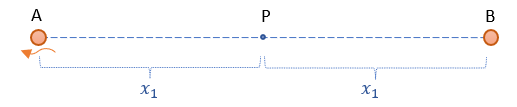
Wygląda sympatycznie, mamy jedno ściśle określone położenie punktu P i nie musimy naginać przestrzeni, żeby opisać zjawisko. Jak wspominałem lubię odwoływać się do najprostszych modeli i można powiedzieć, że teraz nasz punkt P zamiast na dwóch patyczkach, porusza się na gumce rozciągniętej miedzy obiektami A i B. (Czyli uzyskujemy jedną przestrzeń zgodną z tą w kosmologii i już niepotrzebne byłyby dwie: wynikające z ruchu obiektów i ekspansji wszechświata.) A jakie otrzymamy w tym przypadku równania ruchu?
Okazuje się (wyprowadzenie tutaj), że wcześniejsze wzory transformacyjne przybierają teraz następującą postać:
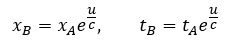
W efekcie niniejszych zależności nie mamy ograniczeń na maksymalną prędkość, bo u może być tu dowolnie większe od c i wreszcie prędkości dodają się z zwykły sposób u1+u1=2u1.
Ale czy te formuły mogą być użyte zamiast wszechstronnie sprawdzonych zależności relatywistycznych?
No przecież to są te same wzory. Zauważmy, że podczas dokonywania omawianych korekt w Transformacji Lorentza zmieniła się także definicja prędkości, którą można wyrazić następującym wzorem (wyprowadzenie tutaj i tutaj):
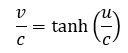
Po podstawieniu tak wyrażonej prędkości do wzorów Lorentza otrzymujemy:
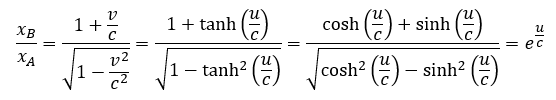
Jak widać, do celow rachunkowych te wzory mogą być stosowane równoważnie. (Każda konwencja jest dobra jeśli potrafimy zapewnić spójność obliczeniową i będziemy konsekwentnie się do niej stosować.) Różnica jest w wyobrażeniu mechanizmu zjawiska i jego istoty oraz zapewne postrzeganiu naszych ograniczeń choćby w kontekście maksymalnej prędkości w przyrodzie.








Komentarze
Pokaż komentarze (5)