Ostatnio znów zachwycają mnie torusy. Chciałam przedstawić Wam urodę modelu torusa.
Na początek 1. torus - biała dędka:

Dętka - komora z elastycznego materiału (najczęściej z gumy), wypełniona gazem (najczęściej powietrzem) tłoczonym poprzez wentyl. Jej zadaniem jest utrzymywanie ciśnienia gazu wypełniającego przedmiot ją zawierający, a przez to zapewnienie mu pożądanych właściwości użytkowych - przede wszystkim sprężystości. Co może niektórym wydawać się dziwne, dętki z czarnej gumy były produkowane bez póżniejszych matematycznie skomplikowanych konstrukcji, takich jak ta:
2. Torus z trzema współrzędnymi

A ten 3. torus już jest nawet animowany czyli jego elementy znajdują się w ruchu:

Tu podobny, też ruchome są jego części. Ten to ma nawet właściwości "hipnotyzujące", czyż nie?

Ciekawe, czy istnieje mozliwość powstania osobliwości w samym centrum takiego torusa?
Ten następny to torus wrzecionowy. Część ścianki została usunięta, by możliwe było zajrzenie do jego wnętrza.
4. We wnętrzu tego torusa znajduje się wrzeciono.

Lużne skojarzenie:
Metryka Kerra– ścisłe, stacjonarne i osiowosymetryczne rozwiązanie równania Einsteina ogólnej teorii względności w próżni opisujące geometrię czasoprzestrzeni wokół obracającego się ważkiego ciała. Zostało ono znalezione w 1963 przez Roya P.Kerra, nowozelandzkiego matematyka[1].
Zgodnie z tą metryką obracające się ważkie ciało powinno wykazywać efekt Lensa-Thirringa przewidujący, że materia w pobliżu masywnego wirującego obiektu musi się również obracać. Obrót taki nie jest spowodowany przez jakąkolwiek działającą na takie ciała siłą, lecz krzywizną czasoprzestrzeni. Metryka Kerra jest uogólnieniem metryki Schwarzschilda, opisującej geometrię czasoprzestrzeni wokół doskonale sferycznego, nieruchomego i obojętnego elektrycznie ciała. Innym tego typu rozwiązaniem jest odkryta w latach 1916–1918 metryka Reissnera-Nordströma. Metryka ta opisuje geometrię czasoprzestrzeni wokół nieruchomego, sferycznego ale naładowanego elektrycznie ciała. W 1965 zostało odkryte najogólniejsze spośród tych trzech rozwiązań. Jest to metryka Kerra-Newmana, opisująca geometrię czasoprzestrzeni wokół obracającego się, naładowanego elektrycznie ciała. Relacje między tymi czterema metrykami są przedstawione w poniższej tabelce. ( Z wikipedii)
5. A tu pajęczyna fragmentu spłaszczonego torusa:

6. I ten sam fragment w innej postaci graficznej:

Te pasy kolorowe kojarzą mi się z liniami sił w polu elektromagnetycznym.
7. Tutaj jeszcze inny torus "tęczowy":
8. I jego fragment:

9. I pod innym kątem:
A tu animacja:www.google.com/imgres
10. I jeszcze jeden taki torusik, co to do galaktyki podobny:

11. I torus niebiański:

A słowo torus z łaciny pochodzi i podobno znaczyło: poduszka. Wyobrażacie sobie torusową podusię?
12. I jeszcze taka grafika torusowa (projekt w sam raz na koszulki lub pidżamki):

Miłych snów.
p.s. Grafiki nie są mojego autorstwa. Znalazłam je szperając w internecie.
p.s.2) Moim zdaniem eliptyczny kształt galaktyk wynika z obrazu spłaszczonego i nachylonego pod pewnym kątem względem nas (obserwatorów) torusa.. I być może odkrywam największe "oczywistości". Ale przyznaję, że to bardzo miłe móc samej (samemu) takich odkryć dokonywać.
Dodatek.
Doczekałam się (wymarzyłam) pięknej animacji, którą znalazłam w angielskiej wersji Wikipedii. Cudeńko. Torus przekształca się w PODWÓJNĄ SFERĘ...
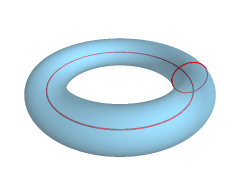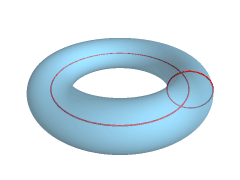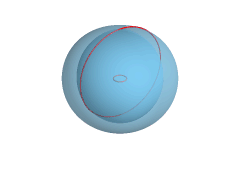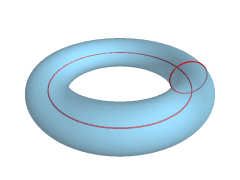
I druga animacja - sprowadzenie torusa do płaszczyzny 2D:

zródło:
http://harmonicresolution.com/Toroidal%20Space.htm

" Rzeczywistość składa się z nieskończonego strumienia interpretacji postrzegania, które my, jednostki posiadające specyficzne członkostwo nauczyliśmy się odczuwać jako oczywiste. (...) Nasz odbiór rzeczywistości jest przez nas uznawany za tak niepodważalny, że podstawowe założenie magii traktujące go jedynie jako jeden z wielu opisów, niełatwo przyjąć poważnie."
" Don Juan - człowiek wiedzy i nauczyciel Carlosa Castanedy. -------------------------------------------------
dodatek z dnia 13.09.09
"Każdy człowiek tworzy swoją osobistą historię ze swojej własnej i jedynej w swoim rodzaju perspektywy. Po co w takim razie narzucać innym swoją wersję, jeśli będzie ona dla nich nieprawdziwa? Kiedy to zrozumiesz, nie będziesz odczuwać potrzeby obrony tego, w co wierzysz. Nie jest ważne to, aby mieć rację i dowieść innym, że są w błędzie. Postrzegaj każdego człowieka jako ARTYSTĘ, kogoś, kto ma ci do opowiedzenia jakąś historię. Wiedz, że to, w co wierzą inni, jest po prostu ich punktem widzenia, i że nie ma to z Tobą nic wspólnego." Don Miguel Ruiz
-------------------------------------------------
--------------------------------------------------
Moje notki "unifikacyjne":
1. Geometria kwantowa 1
2. Geometria kwantowa 2
3. Geometria Kwantowa 3 -wstęp do kwantowej grawitacji
4. Geometria kwantowa 4
5. Torusy
6. Prędkość grawitacyjna a stała Plancka
7. Kwanty światła i eter - część I.
8. Kwanty światła i eter - część II.
pozostałe notki w polecane strony
Nowości od blogera
Inne tematy w dziale Technologie

