"Moment pędu definiuje się jako pseudo wektor będący wynikiem iloczynu wektorowego wektora położenia i pędu"
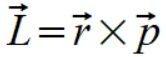(1)
Taką suchą definicje można znaleźć w wielu źródłach ale coś mi w niej zawsze brakowało. Czym właściwie jest ten wektor i co on odwzorowuje w rzeczywistości? Jest to twór czysto abstrakcyjny, czy może jest ukryte coś więcej? Jaki układ odniesienia stosować? Oczywiście z czasem używania tego wektora niejako intuicyjnie można dojść do wniosku, że najlepszym układem odniesienia jest układ z początkiem w środku ciężkości, ale dlaczego akurat ten układ odniesienia jest najlepszy? Czym różni się wektor położenia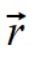 
względem środka ciężkości od wektora położenia 
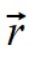względem innego punktu? Długo szukałem tej odpowiedzi w literaturze, w internecie czy pytając po prostu Fizyków ale bez powodzenia. Nie dość że nikt nie posiadał takiej wiedzy to jeszcze nikt nie był zainteresowany poszukaniem odpowiedzi. Być może ktoś już kiedyś to pokazywał ale wiedza ta została uznana za nieprzydatną i po prostu się jej nie używa.
Popatrzmy jak działa wektor momentu pędu na wirujących dwóch masach m1=m2 =1, pamiętając o prawie zachowania momentu pędu czyli niezmienności tego wektora w czasie
(2)
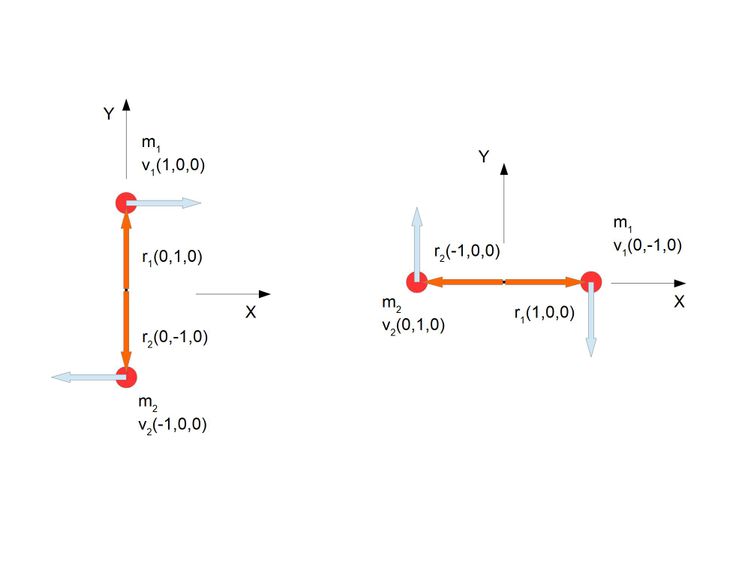
Wektor momentu pędu dla układów złożonych jest to suma wektorów pędu jego elementów
(3)
Czyli w naszym układzie odniesienia z początkiem w środku ciężkości mamy
L= m1 (r1 x v1) + m2 (r2 x v2)
W chwili początkowej (pierwszej) mamy Lp=(0,0,-2) , w chwili końcowej (drugiej) mamy Lk=(0,0,-2). Jak widać wynik zgodny z oczekiwaniem (2) moment pędu jest stały w czasie.
Sprawdzamy więc inny układ odniesienia przesunięty o 1 na osi X, czyli odejmujemy 1 do każdego wektora położenia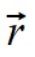 
na współrzędnej x, wektory prędkości nie ulegają zmianie. Mamy w pierwszej chwili r1(-1,1,0); r2(-1,-1,0) i w drugiej końcowej chwili r1(-2,0,0); r2(0,0,0)
Jak się okazuje w pierwszej chwili mamy Lp1=r1xp1=(0,0,-1) i Lp2=r2xp2=(0,0,-1). Oraz w chwili drugiej Lk1=r1xp1=(0,0,-2) i Lk2=r2xp2=(0,0,0). Sprawdziłem dla różnych układów odniesienia i jak się okazuje dla obliczeń momentu pędu dla całego układu jest nieistotne jaki układ odniesienia przyjmiemy (nieruchomy względem środka ciężkości) wynik pozostaje niezmienny.
Czy więc dobór układu odniesienia nie ma tu znaczenia? Sytuacja się zmienia kiedy chcemy analizować nie całość a część układu. Przyjęcie innego układu odniesienia dla obliczenia momentu pędu dla pojedynczych elementów, najczęściej daje różne wartości momentu pędu i może też skutkować tym że moment pędu tego elementu nie jest stały w czasie. W naszym przykładzie w pierwszym przykładzie widać że przesunięcie układu odniesienia nic nie zmienia, czyli jak widać istnieje możliwość znalezienia różnych układów odniesienia które dają poprawny wynik. W drugim przykładzie licząc pojedyncze elementy widać już różnice, momenty pędu pojedynczych elementów zmieniły się względem pierwotnego układu odniesienia, ale tez wektory te nie są stałe w czasie dla tych elementów, mimo że rotują wokół siebie w sposób stabilny i nie ma tu żadnej transformacji energii czyli wykonywania Pracy.
Rozpatrując moment pędu pojedynczego elementu względem środka ciężkość jest on stały w czasie.
I teraz podstawowe pytanie, i co to zmienia? Przy liczeniu całego układu nic, jednak kiedy analizujemy momentów pędów poszczególnych elementów najlepiej jest to robić względem środka ciężkości, gdyż w moim odczuciu które dopiero trzeba udowodnić taki moment pędu jest najbliższy prawdy, a przyjęcie innego układu odniesienia może (nie musi) dać nam abstrakcyjne odwzorowanie rzeczywistości.
Niby nic wiele ale postawienie takiej tezy znacząco zawęża pole moich poszukiwań. Odrzućmy na chwilę tezę że nie istnieje uprzywilejowany układ odniesienia i wróćmy do źródeł mechaniki klasycznej, że jednak istnieje jeden prawdziwy układ odniesienia tak zwany eter. Teoretyzujemy, możemy wszystko. Poruszając się na przykład na karuzeli jak poniżej, mimo że koło porusza się ze stałą prędkością względem swojego środka, to siedzący na niej ludzie odczuwają przeciążenia zgodnie z układem odniesienia ziemi. Mimo że koło się kręci a ramie chusta, są momenty kiedy osoba na niej siedząca przez chwile jest nieruchoma względem ziemi i nie czuć wtedy przeciążeń, wiem sprawdziłem na własnej skórze, jak ktoś nie wierzy niech sam spróbuje.
Tak samo patrząc na gwiazdy, musimy mieć świadomość że względem nas zataczają one okręgi o promieniach miliardów lat świetlnych zaledwie w 24 godziny. Jeżeli nasz układ odniesienia miał by być równie dobry jak każdy inny, to musiały by na te gwiazdy działać niewyobrażalnie wielkie siły dośrodkowe (oraz ogromne przeciążenia) aby je na tych orbitach utrzymać. Dlatego też teza że dobór układu odniesienia nie ma znaczenia może i jest poprawna matematycznie, to jednak w rzeczywistości eksperymenty pokazują że na przykład pasażer karuzeli odczuwa działanie sił względem ziemskiego układu odniesienia, który jest tym można powiedzieć prawdziwym (inercjalnym), a nie sił względem na przykład środka tego koła na podstawie którego wyliczone siły są tworami abstrakcyjnymi.
Nie chce tu wchodzić w dyskusje czy eter istnieje czy też nie, bo nie taki jest cel tego wywodu, a chciałem jedynie zauważyć że mechanice klasycznej jak i w eksperymencie, jednak wciąż bardzo ważne jest dobranie właściwego układu odniesienia.
Wracając do tematu, skoro założyłem tezę że układ odniesienia jednak jest ważny, to czym jest wektor momentu pędu i dlaczego powinniśmy go liczyć od środka ciężkości. Wektor położenia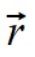 
jest dla mnie wektorem względnym, w ruchu obrotowym realne dla mnie jest prędkość punktów v i siły dośrodkowe F które utrzymują punkty w ruchu obrotowym. Jak więc wektor siły ma się do wektora położenia? Oczywiście siła to przyspieszenie razy masa F=am, a że rozpatrujemy sytuacje gdzie masa jest stała, to interesuje nas przyspieszenie dośrodkowe i ma ono następującą relacje do wektora położenia względem środka ciężkości.
(4)
czyli
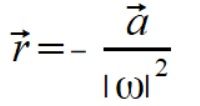(5)
Używając wzoru na wektor momentu pędu (1) za wektor położenia wstawiamy wektor przyspieszenia dośrodkowego (5)
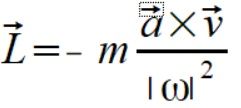(6)
prędkość kątowa to
(7)
Chcemy wiedzieć czym jest wektor momentu pędu i nieistotny jest dla nas obecnie orientacja wektora w przestrzeni, dlatego przechodzimy z zapisu wektorowego na proporcjonalny pamiętając że
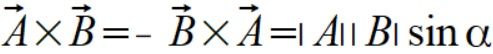(8)
gdzie alfa jest kątem między wektorami.
Zauważmy że w naszym przypadku kąt między wektorami a i v równa się α, a ponieważ wektor położenia r jest skierowany w przeciwnym kierunku (obrócony o 180 stopni), to kąt między r i v to α+Π. Czyli sinα a i v to -sinα r i v.
wstawiając więc wzór na prędkość kątową (7) do wzoru na moment pędu (6) i zmieniając zapis z wektorowego na proporcjonalny (8) mamy
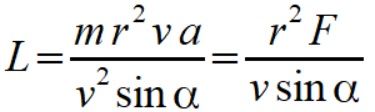(9)
v sinus kąta między r i v, to składowa wektora prędkości prostopadła do wektora położenia, czyli składowe prędkości liniowej równoległe do wektora położenia nie wpływają na wektor momentu pędu.
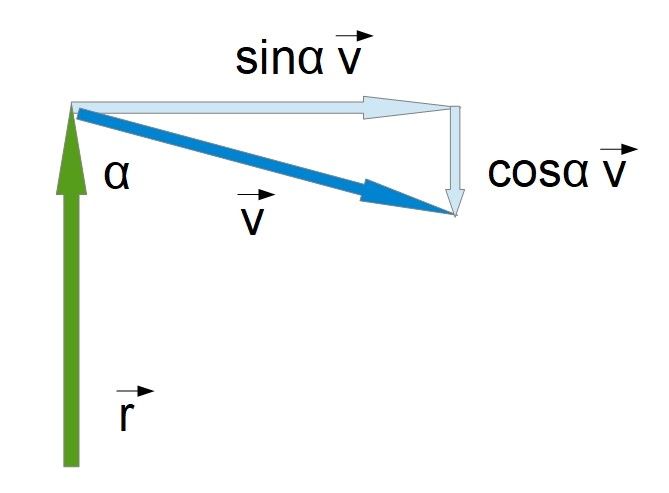
Zapytacie po co taki niewygodny wzór na kręt (9) skoro mamy jego bardzo prostą postać (1). Dla mnie (9) dużo więcej mi wyjaśnia czym jest wektor L. W (1) mamy wektor położenia 
który jest względny w (9) mamy siłę która jest siłą dośrodkową (wynika to z (5)) co wskazuje nam że właściwym układem odniesienia jest środek masy, gdyż w tym układzie siły dośrodkowe mają najprostszą postać, a doskonałość natury można poznać po jej prostocie. Po za tym we wzorze tym mam to czego szukałem, zależność wektora momentu pędu od prędkości punktu i siły więzów i jak się okazało ważny jest jeszcze kwadrat odległości od środka ciężkości.
Dodatkowo kiedy przyjmiemy się wzorowi (9) wiedząc że r jest wektorem położenia i F to siła centralna, od razu przychodzi skojarzenie ze wzorem na energie potencjalną
(10)
oraz wzór na prędkość polową
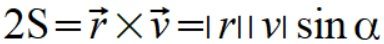(11)
czyli nasz wzór proponuje zapisać używając (10) i (11)
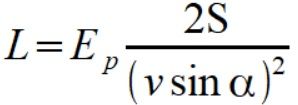(12)
Kręt jest to energia potencjalna wynikająca z siły więzów (nie koniecznie to samo co energia potencjalna siły grawitacji) oraz podwojona prędkość polowa przez kwadrat składowej prostopadłej do wektora położenia wektora prędkości kątowej.
Czy te moje kombinacje na coś się przydadzą? Zobaczymy. Wydaje mi się że teraz mamy nowe spojrzenie czym jest wektor momentu pędu i łatwiej nam będzie zrozumieć mechanizm działania prawa zachowania momentu pędu i uzupełnić mój dowód.
https://www.salon24.pl/u/przestrz/833687,wyprowadzenie-rownania-momentu-sily-wewnetrznych
