Chyba ciężko będzie znaleźć osobę, która poznawszy pojęcie pochodnej cząstkowej nie potwierdzi znanej prawdy, że:
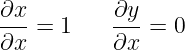
Czując co się święci, ktoś podejrzliwy od razu zauważy: „Ale nie napisałeś czym są x i y”. OK. No to spróbuję napisać. Mamy kawałek płaszczyzny – inaczej: dziedzina funkcji, które będziemy różniczkować będzie dwuwymiarowa. Na tym kawałku płaszczyzny korzystamy z dwóch zmiennych: x i y.
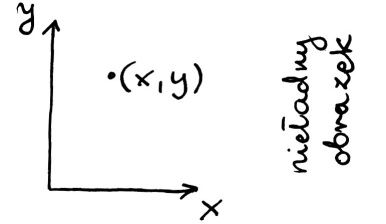
Teraz nie powinno być wątpliwości, że naprawdę:
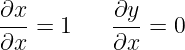
Zresztą tak właśnie chce definicja, zacytowana obrazkowo w poprzedniej notce.
No to teraz nie zmienię nic w powyższym przykładzie, a jedynie dla zgrywy, x nazwę sobie p, a y – V. W końcu to jedynie zmiana nazwy i nie powinna mieć wpływu na zachowanie modelu. Wtedy powyższa formuła przepisze się następująco:
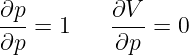
Ci, co liznęli nieco termodynamiki chyba nie zgodzą się, że te równania są zawsze prawdziwe. Bo poprzez p oznaczamy zwykle ciśnienie, a V to objętość. Drugie równanie oznaczałoby wtedy, że przy zmianie ciśnienia objętość nigdy się nie zmienia.
„No zaraz, zaraz” ktoś zakrzyknie: „Przecież x i y to zmienne na płaszczyźnie, a p i V to wielkości fizyczne – to zupełnie inna para kaloszy!” No właśnie nie. To taka sama para kaloszy.
Gaz doskonały
Może tego nie widać od razu, ale model gazu doskonałego (przy stałej liczbie moli n) spełnia warunki, jakie wypisałem na początku. Każdy stan można opisać za pomocą trzech liczb: p, V, T. Tyle, że nie są one niezależne, bo przecież według równania Clapeyrona:
pV/T = nR
Tak więc budując przestrzeń stanów takiego gazu, dostajemy dwuwymiarowy zbiór, czyli ni mniej ni więcej – kawałek płaszczyzny. Do jego pełnego opisania wystarczą dwie zmienne. Jak widać model jest równoważny temu, w którym stosowaliśmy x i y.
Najczęściej używa się p i V, ale nic nie stoi na przeszkodzie, by wybrać p i T, albo V i T. Zresztą jak wyliczymy sobie entropię S, będzie ona równie dobrą zmienną jak trzy poprzednie:
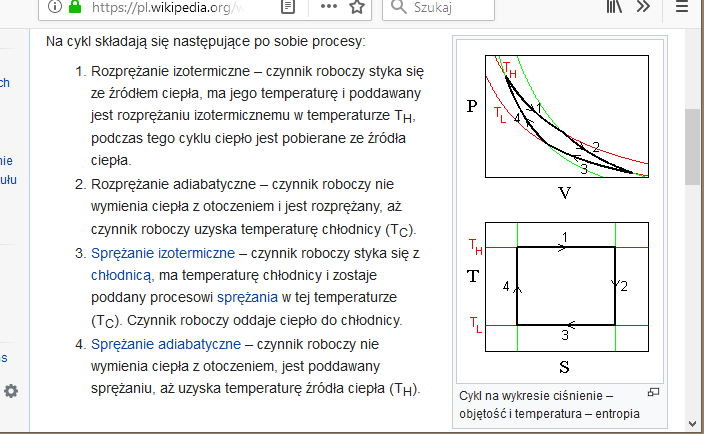
Ten sam cykl Carnota na dwóch obrazkach,
w dwóch różnych układach współrzędnych
Zanim wrócimy do matematyki, zastanówmy się, nad fizycznym sensem wzorów:
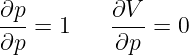
Wyrażenie różnicowe ΔV/Δp informuje nas o tym, jak zmienia się objętość (V) przy okazji zmian ciśnienia (p). Czyli będzie ono równe zero, gdy objętość się nie zmieni. Z lekcji fizyki powinniśmy pamiętać, że istnieje również taka możliwość. Nazywa się to, że mamy do czynienia z przemianą izochoryczną – objętość gazu pozostaje stała – i wtedy ΔV=0. W każdej innej przemianie tak nie będzie. Skoro tak, to może nie da się zdefiniować pochodnej cząstkowej dla funkcji których dziedziną jest kawałek płaszczyzny będącej zbiorem stanów gazu doskonałego?
Da się. Przesuwając uzasadnienia definicyjne do następnej notki, skupię się na praktycznej części liczenia pochodnych cząstkowych. Otóż do określenia jak działają pochodne, musimy na początku wybrać zestaw funkcji tworzących układ współrzędnych.
Wybierzmy przykładowo zestaw {p, V}. Całkiem zaawansowani matematycy powiedzą, że z atlasu wybierają mapę {p, V}, ale dla nas starczy informacja, że będziemy stosować pochodne cząstkowe dla tego, konkretnego układu współrzędnych {p, V}. W praktyce oznacza to, że jeśli będziemy różniczkować po p, to traktujemy V jak stałą – czyli w jakimś sensie uogólniamy cytowaną w poprzedniej notce procedurę, poza współrzędne kartezjańskie. Analogicznie dla różniczkowania po V, p zachowuje się jak stała. Żeby pokazać, która wielkość „jest stała” wymyślono następujący zapis:
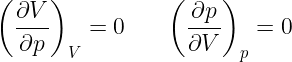
W ramach treningu zróżniczkujmy T. Z równania Clapeyrona dostaniemy T:
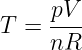
I zakładając, że wybranym układem współrzędnych jest {p, V}, wyliczam:
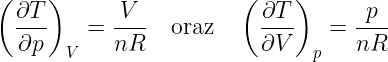
Gdybym jednak wybrał układ {p, T}, wtedy
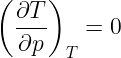
Jako zadanie ZTS można policzyć sobie inne pochodne cząstkowe w innych układach współrzędnych.
Zmienna?
W notce bardzo niechlujnie szafowałem pojęciem „zmienna”. Przepraszam i się poprawiam: – zastosowane symbole: p, V, T, x i y są funkcjami, jedynie dla niepoznaki nazwanymi „zmiennymi”. Nie będę na razie tego uzasadniał, ale jeśli gdzieś spotkasz wyrażenie tego typu:
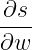
to wiedz drogi czytelniku, że wielkości s i w muszą być funkcjami. Czyli we wzorze:
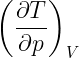
symbole T i p (zresztą V również) oznaczają funkcje. Piszę o tym, bo pozostając przy sformułowaniu „zmienna” wyszłoby, że liczymy pochodną zmiennej, co nie brzmi dobrze, bo przecież różniczkujemy zwykle funkcje. Może zresztą „pochodna zmiennej” da się jakoś uzasadnić, ale jakoś mi to nie pasuje językowo.
(dopisane po dyskusji z Bjabem) Czyli x i y z nieładnego obrazka z początku notki, to dwie funkcje, których dziedziną jest kawałek R2:
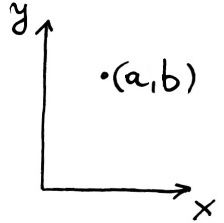
x: (a,b) ↦ a
y: (a,b) ↦ b
Podsumowanie
Wracając do początkowych formuł:
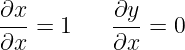
Będą one prawdziwe – to znaczy ta druga formuła, bo pierwsza jest prawdziwa „zawsze” – jeśli wybierzemy układ współrzędnych {x, y}. Dla innego układu
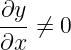
Innymi słowy, pochodna (∂/∂x) zależy nie tylko od x, ale również wyboru funkcji „towarzyszącej”.
Znaczenie funkcji „towarzyszących” stanie się (mam nadzieję) jasne, gdy w następnym odcinku skupię się na interpretacji geometrycznej pochodnej cząstkowej.







Komentarze
Pokaż komentarze (21)