Wektor Riemanna-Silbersteina z przedziałkiem z boku przestaje straszyć

Kto ciekaw jak to jest z duchami-przyczepkami, może poczytać sczegółowy opis takiego jednego przypadku:

"SPIRIT RELEASEMENT THERAPY"
Dr. Alan Sanderson MBBS (London) MRCP DPM MRCPsych

Gladys zmarła przepełniona zlością i przyczepiła się od samego poczatku przy narodzinach Klary. I rujnowała Klarze życie (Klara i tak miała problemy z rodzicami) . W końcu udało sie terapeucie przekonać Gladys by złość zostawiła w ciele i odeszła jako czysty duch ku światłu w pokoju.

Duch wektora Riemanna-Sielbersteina jest podobnie złośliwy. Riemann miał być teologiem, nawet teologię studiował. Jednak wybrał matematykę i słusznie uczynił. Był introwertykiem, a matematyka to dla takich świetna terapia. Nie wiem na ile się zasłużył w kreacji wektora Riemanna-Sielbersteina (RS). Tak czy siak dziś wektor RS straszy i wypada z nim poważnie porozmawiać. Przekonać go by poszedł sobie do światła.

A w czym problem? Otóż chciałoby się ze stanami kwantowymi fotonu powiązać jakoś pola elektryczne i magnetyczne. No chciałoby się i tyle. I w tym celu niektórzy fizycy przywołują duchy, takie jak ten wektor RS. Nie to, że nie dałoby sie i bez duchów. Dałoby się. O tym w kolejnych notkach. Ale z duchem ciekawiej. A w dodatku  jeśli duch nosi takie piękne imię: Riemann-Sielberstein. Taki duch musi rodzić respekt i podziw. I budzi. Czy zasłużony? To inna sprawa. Jak problem można rozwiązać i bez ducha - o tym kiedy indziej. Dziś kontynuujemy notkę poprzednią "Duch Riemanna-Silbersteina czeka na uwolnienie". Duch RS wywołał słuszny niepokój Bjaba nie dając spać po nocy. Przywołajmy go zatem teraz do spokoju.

Czemu duch RS straszy? Bo musi. Nie może nie straszyć. Taka jest już jego natura. Póki się tu pęta - będzie straszył. Mówi o tym twierdzenie Brouwera (nasz Borsuk też się tym parał): na dwuwymiarowej sferze nie da się wprowadzić gładkiego nigdzie nie znikającego pola wektorowego. Nie da się zaczesać włochatej piłki bez pozostawienia wiru choć w jednym punkcie. Na sferze trójwymiarowej by się dało. Ale na dwuwymiarowej - się po prostu nie da. Tak mówi Pani Profesor Topologia, a z nią żartów nie ma.

Wektor Riemanna-Sielbersteina wymaga zaczesania sfery. Sfery zaczesać się nia da bez osobliwości. Zatem i wektor RS będzie miał osobliwości. Nie ma rady - upiór będzie straszył. Idzie o to by się go nie lękać.

Teraz detale, które uspokoją nie mogącego spać Bjaba. Przyjrzyjmy się wzorowi (3.3), który tak niepokoił Bjaba:

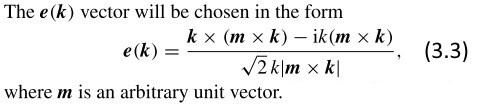
Pyta fryzjer klienta: "Gdzie przedziałek? Po lewej, po prawej, czy może pośrodku?"
"O nie!" Woła klient. Tylko nie pośrodku!

Nasz klient nasz Pan. Wybór wektora m to wybór przedziałka. Nie chcemy by przedziałek wypadł tam, gdzie go nie chcemy. Nie chcemy go dziś na osi z. Prosimy fryzjera, by pojawił się na osi x, ta nam dziś nie przeszkadza. W porządku, mówi fryzjer, zatem wybieram za m wektor m=(1,0,0). Może być? Oczywiście, że może  I już mamy formułę:

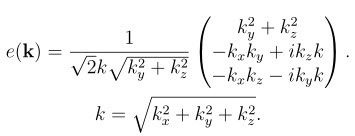
Teraz przypuśćmy, że  k jest na osi z, zatem k=(0,0,k_z), wtedy natychmiast otrzymujemy stąd

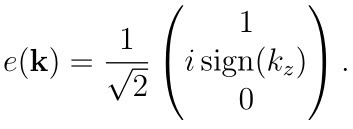
Wyjaśniliśmy zatem kolumienkę o której szła dyskusja pod poprzednią notką. Jak stąd dostać zależność od położeń i pędów? O tym w kolejnej notce.

Są dwa główne grzechy ludzkie, z których wypływają wszystkie inne: niecierpliwość i zaniedbanie. Z niecierpliwości ludzie są wyrzucani z raju, z powodu nieostrożności tam nie wracają. A może jest tylko jeden wielki grzech: niecierpliwość. Z niecierpliwości wypędzani, z niecierpliwości nie wracają.

Franz Kafka