Elipsoidalne fikania

Niniejsza notka jest kontynuacją notki Bąk nad Sekwaną Dalej analizujemy zmianę w czasie wektora prędkości kątowej swobodnej bryły sztywnej. Podpieramy się przy tym obrazkiem z wykładu Lesiaka:

By było konkretnie bierzemy bąk asymetryczny z I_X = 3, I_Y = 2, I_Z = 1. Trajektorie wektora ω biegną na przecięciu dwóch elipsoid: elipsoidy stałej wartości krętu J² i stałej wartości energii. Jak te trajektorie wyglądają?

Przypomnijmy z poprzedniej notki, że dla elipsoidy stałego krętu długości półosi wynoszą:

a = √(J²) /I_X, b = √(J²) /I_Y, c = √(J²) /I_Z

Zaś dla elipsoidy stałęj energii kinetycznej

a = √(2T/I_X) , b = √(2T/I_Y) , c = √(2T/I_Z).

Gdy J² jest dane, energia kinetyczne nie może być zbyt mała. Inaczej elipsoidy się nie przetną, ruch będzie niemożliwy. Najmniejsza wartość energii kinetycznej jest wtedy, kiedy najkrótsza półoś elipsoidy energii jest równa najkrótszej półosi elipsoidy krętu:

√(J²) /I_X = √(2T/I_X)

czyli 2T_min = J²/I_X

Największa możliwa energia to taka, gdy najdłuższa półoś elipsoidy energii równa jest najdłuższej półosi elipsoidy krętu:

2T_max = J²/I_Z

Pomiędzy tymi skrajnymi wartościami energii kinetycznej leży wartość specjalna:

2T_spec = J²/I_Y

By być konkretnym, weźmiemy J² = 10. Wtedy, zakładając I_X = 3, I_Y = 2, I_Z = 1, mamy

2T_min = 10/3 = 3.333.., 2T_max = 10/1 = 10, 2T_spec = 10/2 = 5

Czas na rysunki i na omówienie tego co się dzieje. Przy maksymalnej energii kinetycznej nasz asymetryczny bąk obraca się względem najdłuższej osi (o najmniejszym momencie bezwładności). Dwie elipsoidy stykają się jedynie w dwu punktach. Wektor prędkości kątowej jest stały. Niby mówi się o tym, że jest to sytuacja stabilna, ale bąk gdy tylko będzie miał okazję to się swojej energii kinetycznej pozbędzie. Oto obrazek dla 2T=10-0.2, czyli gdy się pozbył 0.1 energii kinetycznej:

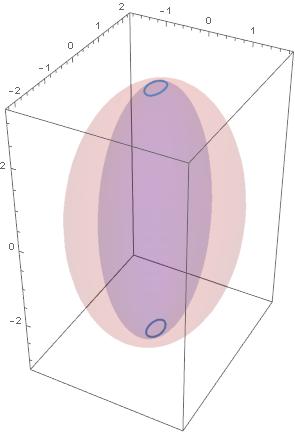
Ta niebieskawa elipsoida, to elipsoida stałego krętu, ta czerwonawa, tu pękata, to stałej energii. Widać, że oś obrotu podlega małej precesji, albo wokół jednego bieguna na długiej osi, albo wokół drugiego – to te dwa kółka. Z obrazka nie wiemy jak długo taka precesja trwa.

Druga skrajność to stabilny obrót wokół najkrótszej osi. W jedną lub w drugą stronę. Energia kinetyczna jest wtedy najmniejsza, już mniejsza, przy danej wartości krętu, być nie może. Zanim jednak stanie się najmniejszą, przedtem jest stadium precesji wokół najkrótszej osi, jak na obrazku poniżej dla 2T = 3.333+0.1

 

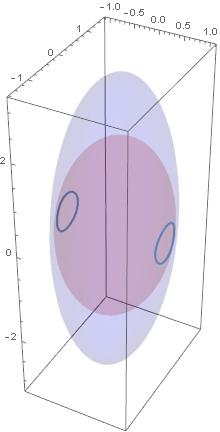
A co pomiędzy tymi skrajnościami? Pośrodku między tymi skrajnościami jest obrót wokół środkowej osi. Dla 2T_spec = 5 dwie elipsoidy, elipsoida krętu i elipsoida energii przecinają się wzdłuż dwóch elips:

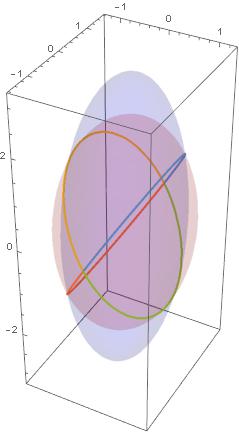
Oś obrotu wędruje od jednego bieguna do drugiego bieguna, po połowie elipsy. Z obrazka tego nie widać, Mogłoby wyglądać, że oś obrotu wędruje po elipsie. Jednak czas przejścia od jednego bieguna do drugiego okazuje się być nieskończonym. Czyli w skończonym czasie do bieguna nie dojdzie. Całe życie bąka to jeden długi fik, bez końca. Na obrazku mamy więc cztery fiki.

Dobrze jest zobaczyć co się dzieje w przypadku gdy energia kinetyczna jest trochę większa lub trochę mniejsza od tej pośrodkowej. Dla trochę większej mamy:

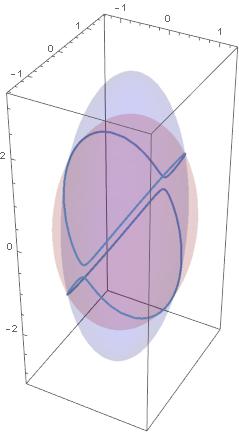
Taki fik od prawie jednego bieguna środkowej osi do prawie drugiego bieguna tej osi, i tak w kółko – fikanie bez końca.

Podobnie dla trochę mniejszej od pośrodkowej

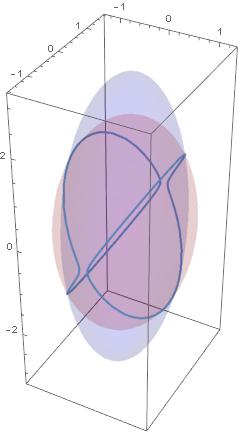
Też fikanie bez końca, tyle, że inna trajektoria. Jak długo trwa taki jeden fik – tego z obrazka nie widać, trzeba na to innych metod.

Tymi innymi metodami zajmiemy się w dalszym ciągu. Zauważmy jednak, że latającego bąka możemy zobaczyć na filmie Prawdziwy Geniusz:

Choć na tym filmie żyroskopy występują co najwyżej w układach naprowadzających lasery.