Grupirowka Antoniego Macierewicza szuka od 10 lat bezskutecznie, w celach czysto politycznych, mechanizmu "zamachu"/"wybuchu" smoleńskiego. Poszukiwania te, którym towarzyszy nieporadność opozycji, ucieczka od tematu w środowisku naukowo-technicznym i lotniczym, oraz znudzenie laików, ciągle trwają i ciągle odgrywają swą niechlubną rolę. Od strony merytorycznej skazane są na infamię i śmiech naukowców. Nie może być inaczej, bo prawdziwi naukowcy którzy zajęli się analizą wypadku, potwierdzili brak przesłanek do teorii alternatywnych, a oficjalne śledztwa mówią niezmiennie, że tupolew PLF 101 nie eksplodował a uległ CFIT-owi. To wiedzą liczni specjaliści zaangażowani w dochodzenia. Nie tylko polscy i rosyjscy, ale ostatnio także zachodni (o ukrywaniu faktu zamówienia, a od 9 miesięcy także treści ekspertyz przez Macierewicza pisałem tutaj). Hipoteza wybuchowego wystrzelenia drzwi jest dla mnie o tyle ciekawa, że jest samosprzeczna nie z jednego, a bardzo wielu powodów. Opiszę fizyczne podstawy fiaska projektu KC PiS i pomocników, takich jak dr Wiesław Binienda i dr Gerardo Olivares, z mało znanych uniwersytetów stanowych w USA. Od ponad dwóch lat próbują wesprzeć błędnie robionymi obliczeniami niefizyczny scenariusz wystrzelenia drzwi 2L tupolewa przez rzekomą eksplozję wewnątrz kadłuba samolotu. Obliczeniami, których nota bene nie opublikowali i nie opublikują, gdyż prawo do tego wg kontraktu zarezerwował wiceprezes partii politycznej.
Rozdział podzielony jest na dwie części. W cz. 1 wyjaśnię dlaczego sam pomysł symulacji "wstrzelenia" drzwi 2L w ziemię na wrakowisku, w miejscu skąd wydobyte zostały spod ziemi drzwi, jest bezsensowny. Zrobię krótki wykład teorii i inżynierii wbijania przedmiotów w ziemię, cytując własne obliczenia łączące dwie rozłączne co do prędkości procesu domeny: inżynierii wbijania pali w ziemię, oraz wbijania w grunt pocisków na poligonach i w laboratoriach.
W cz. 2. zastosuję zasady fizyki wbijania przedmiotów w ziemię do danych eksperymentalnych z poligonu Tonopah w Nevadzie oraz do katastrofy smoleńskiej. Wyjaśnię, dlaczego proponowany przez PiS scenariusz wymagałby wielu wyjętych z kapelusza kryjącego pustą głowę parametrów, m.in. naddźwiękowej prędkości drzwi 2L.
67.1. ZAŁOŻENIA HIPOTEZY WYBUCHOWEJ O DRZWIACH 2L SĄ BŁĘDNE
Konsultanci i członkowie tzw. podkomisji Macierewicza, m.in. były adiunkt Nowaczyk, stwierdzili, że w fala uderzeniowa hipotetycznego wybuchu bomby termobarycznej w kadłubie tupolewa nr. 101 (nie mylić z izobaryczno-termokurczliwą, nakreśloną tutaj 9 lat temu) potrafi nadać drugim lewym drzwiom prędkość 140 m/s (ponad 500 km/h). To pomyłka o więcej niż jeden rząd wielkości, typowa dla karykaturalnie pozorowanych badań naukowych tego grona. Bomba termobaryczna wypełnia mieszanką paliwowo-powietrzną kadłub, po odpaleniu ładunku inicjującego, po czym następuje zapłon mieszanki (ew. przejście od konflagracji do detonacji). Zawartość energetyczna paliwa powoduje dobrze znany fakt, że produkty spalania mieszanki rozlatują się na wszystkie strony z prędkością rzędu 103 m/s, w postaci fali uderzeniowej. Zapisy licznych rejestratorów lotu i dowody procesowe naturalnie zaprzeczają takiej możliwości, ale czy jest zgodna z fizyką i znanymi faktami?
Ponieważ drzwi w celach bezpieczeństwa hermetyzacji kabiny są po zamknięciu wpasowane we framudze tak, że nie mogą z niej zostać wyważone, to hipotetyczny wybuch najpierw porwałby na kawałki i odrzucił większość cienkiego i lekkiego poszycia TU-154M, a nie stosunkowo ciężki zespół framugi i drzwi. Zatem proponowanie, jak to robi podkomisja, że samolot leciał i nagle tylko drzwi 2L wyskoczyły z niego z prędkością 500 km/h, jest śmieszne. Dokładnie tak jednak wyglądają ich prezentacje filmowe i opowieści, które można znaleźć w ciemnych zakamarkach sieci.
Następny niefizyczny aspekt hipotezy to hamowanie prędkości postępowej drzwi w powietrzu. Twierdzi się, aby miało to jakiś związek z realnym położeniem drzwi po katastrofie, iż spadały z wielką prędkością pionową (130-140 m/s) a zaledwie 10-30 m/s w poziomie, zamiast 75 m/s (prędkość pozioma PLF 101). To wymagałoby podobnie (nonsensownie) wielkiej siły oporu powietrza, co w innej podobnej hipotezie Biniendy o locie końcówki skrzydła urwanej na brzozie Bodina na odległość nie więcej niż 12 m. I tu, w przypadku obiektu 2L, wiele lat po kompromitacji "12m", Binienda i Olivares nie potrafili nauczyć się aerodynamiki na tyle, by nie mylić się 10 do 25 razy (pisał o tym niedawno pan Jaworski).
No i w końcu, jaką prędkość uzyskałyby drzwi 2L gdyby nie były mocno zamocowane we framudze? Załóżmy dość karkołomnie, że na na pokład prezydenckiego samolotu wniesiono ~10 kg paliwa w bombie. Pęd całkowity materiału tej dużej bomby po zdetonowaniu w 20-metrowej sekcji kadłuba, ~104 kg m/s, zadziałałby na powierzchnię kadłuba rzędu 200 m2, z której tylko 1%, tj. 2 m2, przypadają na drzwi 2L. Wielowarstwowe drzwi wraz z pokryciami i zamkami mają masę ~100 kg. Otrzymując ~1% * 104 (kg m/s) poleciałyby z prędkością początkową ~1 m/s. Naturalnie, operowałem tu tylko okrągłymi rzędami wielkości i nie uwzględniałem niejednorodnego rozłożenia pędu na wnętrzu kadłuba. Biorąc na to poprawkę przyjąć można, że fala uderzeniowa nie może rozpędzić drzwi 2L do prędkości ponad 101 m/s. Nawet gdyby eksplozja była w stu procentach skierowana tylko na nieszczęsne drzwi, mógłby być problem z osiągnięciem v=500 km/h. Zatem hipoteza o prędkości powyżej 102 m/s jest całkowicie sprzeczna z działaniem fali uderzeniowej postulowanego wybuchu, c.b.d.o.
Dodać można, że drzwi 2L znaleziono zaryte na metr pod powierzchnię ziemi już za pierwszymi śladami spadku odwróconego samolotu na ziemie. Samolot najpierw spadł na ziemię, a potem drzwi 2L zostały w ziemię wciśnięte. Porównajmy to z często słyszanym kłamstwem, że TU-154 miał znajdować się nad tym punktem na wysokości rzędu 15 m!
W końcu, przypomnę zasadniczy fakt, że ok. 100 ekspertów zaprzysiężonych i pracujących pod sankcjami prawnymi dla prokuratur i agencji RP, FR i USA, nie znalazło we wraku ani zapisach rejestratorów najmniejszych śladów eksplozji, która miała rzekomo rozsadzić tupolewa.
67.2. WSTRZELIWANIE OBIEKTÓW W KOMPUTEROWE MODELE GRUNTU
Zarówno wojskowi, jak i inżynierowie i geotechnicy zajmujący się konstrukcjami na palach wbitych w ziemię, znają tajniki oporu jaki stawia ona przy probie wrzucenia lub wbicia pod powierzchnię czegokolwiek. To, co wiedzą i publikują w podręcznikach i artykułach naukowychc cytowanych poniżej, jest sprzeczne z tym, jak dr G. Olivares z uniwersytetu stanowego w Wichita, Kansas, i jego dwaj młodzi pomocnicy, wykonywali zlecenie W. Biniendy i A. Macierewicza. Były to obliczenia numeryczne metodą FEM (program LS-Dyna) tego, jak drzwi 2L zanurzają się w ziemi będąc odpowiednio, precyzyjnie, ustawione boczną krawędzią, a nie na ukos lub 'na płask' (nie wiadomo dlaczego! to jeszcze jedna tajemnicza historia). Jak wspomniałem na wstępie, w cz. 2 tego rozdziału opiszę jak błędne były ilościowo wyniki otrzymane przez nich. Ale jako tło do obliczeń, podzielę się już tu uwagą nt. przyczyn ich niepowodzenia. Istnieje obecnie zgubna tendencja, by biec od razu do komputera, załadować kupiony program, którego działania się nie rozumie (jak pokażę, tak właśnie było), i... uwierzyć wyniki. Nie trzeba wg niektorych rozumieć fizyki procesu, wystarczy przeczytać, co powiedział program. Podkreślam: podkomisarze Macierewicza nie pierwszy raz wpadli w tę pułapkę. Tak jak wówczas, gdy LS-Dyna/Ansys bezsensownie powiedział im, że siła oporu powietrza na końcówkę skrzydła jest 20-25 razy większą, niż możliwa fizycznie dla modelowanego obiektu. W grupirowce to norma. Raz rzekomy projektant Boeinga Wacław "Caracal" Berczyński przyznał mi, że nie zna aerodynamiki.
LS-Dyna nie ma *standardowych* metod by właściwie oddać fizykę procesu wbijania balistycznego w ziemię, z prędkością setek km/h. Ma wielką interakcyjną listę fenomenologicznych modeli materiałowych, z której jako model gruntu konsultanci Macierewicza wybrali ten, który w opisie miał ang. słowo kluczowe soil. Podejrzewam, że słaba znajomość tematu nie pozwolila im z pierwszych latach badań zauważyć, iż takie modele materiałów jak nr. 78, 147, 173, jak i najpopularniejszy 193 oparty o model Druckera-Pragera, nie są właściwe dla badanego problemu, gdyż to modele elasto-plastyczne. Można je stosować do procesów quasi-statycznych, jak np. obciążenie gruntu przez fundament, lub kopanie ogródka łopatą. Lecz nie do zagadnienia wbijania pali pod most lub zgłębienia rakiety w grunt z prędkością 500 km/h. Tam absolutnie konieczne jest uwzględnienie faktu, że grunt nie tylko natychmiast wychodzi daleko poza zakres stosowalności teorii deformacji elastycznych i uplastycznia się (często podlega tzw. fluidyzacji), ale zasadnicze stają się: (a) przyspieszenia inercjalne materiału penetrowanego proporcjonalne do kwadratu prędkości wbijania (naprężenia dynamiczne), jak i (b) przyspieszenia proporcjonalne do pierwszej potęgi prędkości (lepkość wg. prawa Stokesa; terminy te omówię szerzej w dalszej części rozdziału). Tam zatem trzeba by użyć modelu wisko-plastycznego, od słowa ang. viscosity = lepkość, reprezentującego zjawiska zależne od prędkości. LS-Dyna, jedyne narzędzie które służyło podkomisji, nie ma modeli wisko-plastycznych materiału "soil", a tym bardziej modelu z sensownie dobranymi parametrami. Są takie modele tylko dla metali formowanych z dużą prędkością. Modele elasto-plastyczne LS-Dyna, poprzez brak jakiejkolwiek zależności naprężeń hamujących od prędkości, mogą dać grube niedoszacowanie sił oporu i dwu-trzykrotne przeszacowanie głębokości zagłębienia obiektu.
To, że w niedawno anonsowanych obliczeniach grupy z Uniw. Wichita nie ma zależności siły hamowania od prędkości, udało się niedawno ustalić klatka po klatce na jednym z filmów propagandowych Macierewicza panu Michałowi Jaworskiemu. Odsyłam do jego bloga, gdzie podzielił się swymi ważnymi obserwacjami. Przyspieszenie na filmie jest z dużą dokładnością stałe i równe ok. -1000g. To zgodne jest z podaną powyżej interpretacją błędów w pracy Olivaresa. Prędkość początkowa przy uwzględnieniu aerodynamicznego musiała wynosić około 600 km/h (wybuch nie potrafiłby dać drzwiom 2L odpowiedniego pędu. por. 67.1). Obserwacje Jaworskiego wspierają tezę o fiasku obliczeń, która powstała dwa lata temu. Na podstawie wyznaczonych przez Olivaresa, niemożliwych fizycznie, głębokości wbicia drzwi 2L, teza o błędnych symulacjach została zreferowana przeze mnie w dokumencie, przedstawionym na konferencji zespołu sejmowego M. Kierwińskiego.
67. 3. TEORIA I EKSPERYMENTY WSTRZELIWANIA OBIEKTÓW W GRUNT
Od filmów z działu fantasy przejdźmy teraz do tego, jak jest naprawdę. Zajmiemy się mniej szczegółową niż LS-Dyna 3D, lecz za to poprawną fizycznie wersją obliczeń zagłębiania drzwi 2L w grunt smoleński. (Bedą to obliczenia jednowymiarowe zakładające niedeformowalność drzwi, co jest dobrym przybliżeniem stanu powypadkowego; jeśli ktoś chce popróbować obliczeń sam/sama, wystarczy więc skrypt w Pytonie lub arkusz Excel'a). W 1793 r. Laplace rzekł, że nie ma nic praktyczniejszego niż dobra teoria. Zacznijmy więc od ogólnego rozwiązania następującego problemu.
Problem
W ośrodek o gęstości ρ wbija się pionowo, z dużą prędkością początkową v0 , niedeformowalny obiekt o masie M i polu podstawy A. Fazę elastyczną deformacji gruntu pomijamy, rozważamy tylko deformacje plastyczną i opory ścinania (shear stress), które generują siłę oporu ruchu, zależną od głębokości ciała pod ziemią s(t) oraz jego chwilowej prędkości v(t).
Podać zależność głębokości końcowej obiektu od prędkości zderzenia, S(v0).
Założyć, że naprężenie końcówkowe (zmienne w czasie, działające prostopadle do podstawy obiektu o polu A), oznaczane jako σ, zależy od chwilowych wartości s i v poprzez iloczyn funkcji g() i f()
σ = σ0 g(s) f(v).
Funkcje g i f są bezwymiarowe, a σ0 to wartość naprężenia statycznego tuż pod powierzchnią ziemi. Innymi słowy, g(0) = f(0) = 1.
Uwaga: Nie wprowadzamy tu osobno oznaczeń na efekty naprężeń kompresji i ścinania, zapisujemy dla uproszczenia sumę wszystkich realnych sił oporu, zarówno z powierzchni frontowej jak i ze ścian bocznych obiektu, jako naprężenie σ działające na bok o polu A. Naprężenie σ ma jednostkę Pa = N/m2, tak jak ciśnienie. Siła oporu równa jest A σ(s,v).
Rozwiązanie ogólne problemu
Zgodnie z równaniami kinematyki i dynamiki Newtona,
ds = v dt, (1)
M dv/dt = - σ A (2)
Aby uniknąć zbędnych obliczeń nie wymaganych zadaniem (nikt nie pyta nas bowiem o ustalenie zależności s(t), tylko S=s(v) w momencie końcowym, gdy v=0), wyeliminujemy z dynamiki (równ. 2) dt przy użyciu równania kinematyki (równ. 1), otrzymując po separacji zmiennych
v/f(v) dv = - σ0 (A/M) g(s) ds (3)
Całkując obie strony tego równania, dostajemy rozwiązanie ogólne
F(v) := ∫v0 v/f(v) dv = σ0(A/M) ∫s0 g(s) ds (4)
Oznaczyłem tu przez F wartość całki po prędkości; F ma wymiar kwadratu prędkości. Jeśli zależności g(s) i f(v) nie są zbyt skomplikowane i potrafimy wykonać obie całki analitycznie, to równ. (4) daje analityczną zależność s od v, w tym też szukaną informację o funkcji S(v0). Można też rozwiązać łatwo równ. (4) na komputerze.
Rozwiązania szczególne
Wielomianowe zależności oporu od prędkości i głębokości dają ciekawe zastosowania tego równania. Przyjmijmy
g(s) = 1 + s/h, (5)
gdzie h=const. jest stałą opisującą szybkość wzrostu oporu wraz z głębokością (na przestrzeni h naprężenie oporu rośnie o σ0), oraz
f(v) = 1 + J v + c v2, (6)
gdzie podążając za pracą Smitha (1960) współczynnik przy pierwszej potędze prędkości oznaczamy jako J (jedn. s/m), choć moglibyśmy równie dobrze użyć stałej v1 i zapisać Jv jako v/v1. Do fizycznej interpretacji równania (6) powrócimy.
Podstawiając (5) do (4), dostajemy
F(v) = ∫v0 v/f(v) dv = σ0(A/M) [s + s2/(2h)], (7)
To równanie kwadratowe na s jest łatwo rozwiązać, otrzymując ogólne rozwiązanie na s(v) w skrótowej postaci
s(v) = h { -1 + [1 + 2F(v)/(σ0hA/M)]1/2 } . (8a)
s(v) = F(v)/(σ0A/M), jeśli h -> ∞ (siły nie zależą od s) (8b)
Trudniejsze jest znalezienie F(v) poprzez całkowanie lewej str. równ. (4) w ogólnym przypadku (6). Całka ta faktycznie istnieje w postaci analitycznej i używałem takiego rozwiązania znalezionego w słynnej 'Tabeli całek, szeregów i iloczynów' Gradshteyn i Ryzhik (1970). Tu pozwolę sobie ominąć skomplikowaną, choć używającą tylko funkcji elementarnych i trygonometrycznych, postać F(v). Ciekawiej będzie zapoznać się z rozwiązaniami różnych przypadków szczególnych. [Możesz też czytelniku pominąć formuły analityczne, i otrzymać wyniki wprost z numerycznego całkowania a definicji funkcji F(v).]
Stała siła oporu
Najprostszy wybór współczynników to J = c = 0, oraz h -> ∞. Odpowiada stałej sile oporu równej σ0A. Wtedy f(v) = 1, F(v) = ∫v0 v dv = v2/2, a równ. (8b) daje w granicy h -> ∞
s(v) = (Mv2/2) (σ0A)-1 . (9)
Fizyczna interpretacja (9) jest taka, że jeśli siła oporu jest stała, to końcowe zagłębienie w ośrodek stawiający opór σ0A jest równe początkowej energii ciała Mv2/2 podzielonej przez σ0A, gdyż energia = siła * przesunięcie. Siła oporu staje się stała przy powolnej deformacji ośrodka, po przekroczeniu granicy między elastycznością (grunt deformowany sprężyście) a plastycznością. Zgodnie z treścią zadania, pomijamy opis fazy elastycznego przyrostu siły do wartości σ0A. (W analizie kwS nie ma to znaczenia). W historii stały opór plastyczny spotykany jest pod nazwą oporu Robinsa-Eulera (por. rozdz. 4 książki Iskandera i in., 2015).
Siła oporu ~ v
Jednak w przypadku kolizji z granularnym materiałem piaszczystej gleby siła oporu wcale nie jest stała. Dla niezbyt dużych prędkości wbijania słupów w ziemię, Hussein i in (1992) przeprowadzili serię 15 eksperymentów wbijania przez spadek masywnego młota ze zmiennej wysokości. Wyznaczono maksymalną siłę oporu, osobno stacjonarnego i dynamicznego, z następującym wynikiem: część dynamiczna, zależna od prędkości, była niezerowa i proporcjonalna do prędkości obiektu, fdyn(v0) ~ v0. To zaprzecza niezależności f od v, a wskazuje na zależność liniową.
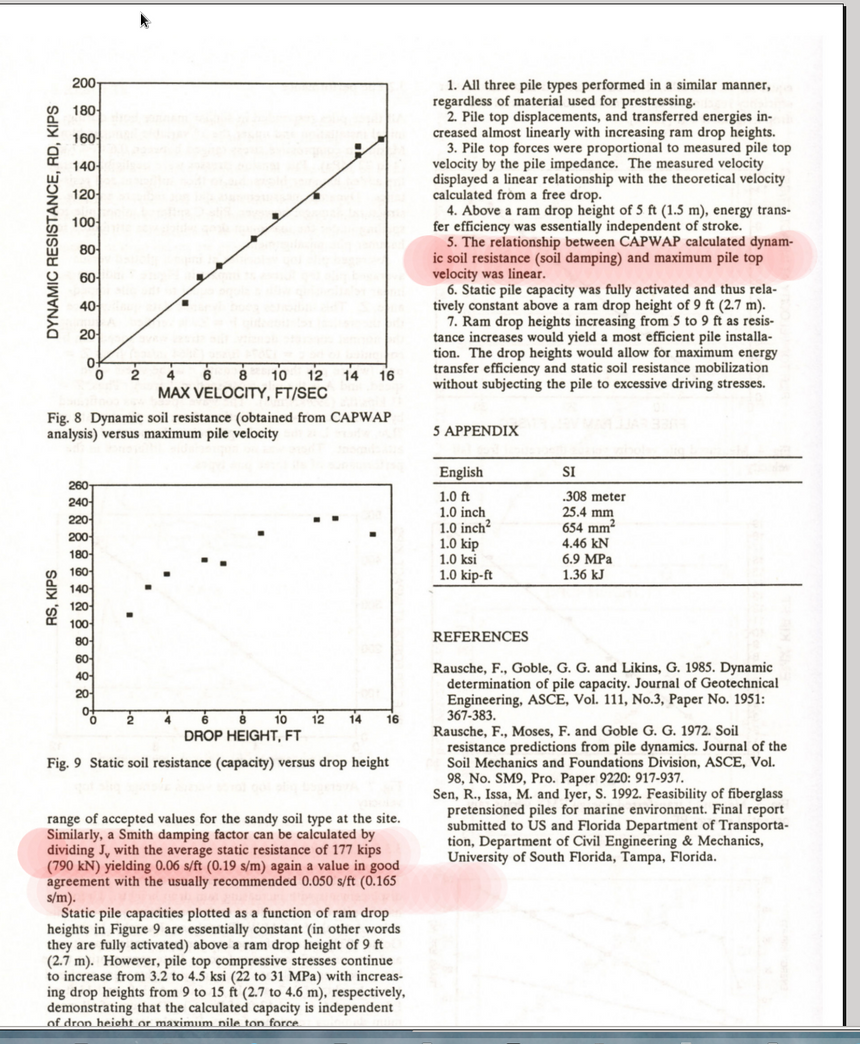
Podsumowania podobnych prac, zgodne z praktyką geotechniczną, są zawarte w książkach o konstrukcjach opartych na palach, takich jak "Piling Engineering" Fleminga i in. (3cie wydanie, 2009). Oto odpowiedni fragment

Od strony fizycznej, takiego rodzaju opór znany jest jako lepkość Stokesa i stosuje się w dynamice ośrodków ciągłych przy umiarkowanych wartościach liczby Reynoldsa. W naszym przypadku takie wartości biorą się z umiarkowanych prędkości wbijanych pali. Gdy c = 0 i występuje w (6) jedynie opór stały i zależny liniowo od prędkości, wówczas
F(v) = ∫v0 v [1 + Jv]-1 dv = [J v - ln (1 + J v)] J-2
Zaniedbując zależność oporu od głębokości, mamy wtedy z równania (7)
s(v) = J-2M/(Aσ0) [J v - ln (1 + J v)] (10)
Logarytm zmienia się wolno wraz z v, zatem nieraz zależność ta przypomina nieco funkcję liniową: s = [M/(J Aσ0)] v - const.
Siła oporu ~ v2
W równaniu (6) mamy składnik proporcjonalny do v2. Ponieważ const*v2/(const*v) rośnie liniowo wraz z wartością v, opór gruntu w przypadku dużych prędkości wbijanych przedmiotów jest zdominowany przez ten ostatni człon. Przy wbijaniu pali w ziemię nie osiąga się prędkości penetracji równej kilkuset km/h, dlatego efekt członu kwadratowego jest tam niezauważalny, odwrotnie niż na poligonach, podczas pomiarów penetracji gruntu przez pociski.
Jaka jest podstawa fizyczna tej części siły oporu dynamicznego, która rośnie z kwadratem prędkości? I. Newton przeanalizował ruch ciał w ośrodku o stałej gęstości ρ, i uznał, że w przedziale czasu dt ciało musi przyspieszyć do prędkości około v początkowo nieruchomy ośrodek o masie równej mniej więcej masie ośrodka w cylindrze o polu podstawy A (gdzie A to nasz przekrój podstawy drzwi) i wysokości v dt. Siła to zmiana pędu podzielona przez dt, a pęd to masa cylindra razy v. Daje to słynne wyrażenie, które stosuje się też do oporu czołowego w aerodynamice:
F_oporu = Cd A ρ v2/2. (11)
Zauważmy, że ρ v2/2 w fizyce cieczy i plastycznych ciał stałych to ciśnienie dynamiczne. Współczynnik oporu Cd jest stały, w przypadku gdy stosunek prędkości ruchu do lepkości kinematycznej ośrodka jest duży. Stała c w równaniu (6) jest równa
c = Cd ρ/(2σ0). (12)
W fizyce i inżynierii nazywamy taką zależność efektem oporu inercjalnego, gdyż wywołany jest inercją ośrodka poruszanego przez obiekt. Gdy występuje stały opór deformacji plastycznej Aσ0 i opór inercjalny, mamy f(v) = 1 + c v2, zaś rozwiązanie naszego problemu głębokości końcowej zagłębienia ma prostą postać (por. (7), (8b)):
F(v) = ∫v0 v [1 + c v2]-1 dv = (1/2c) ln (1 + c v2), (13)
s(v) = M/(2cAσ0) ln (1 + c v2), czyli (14a)
s(v) = M/(CdρA) ln (1 + c v2). (14b)
Rozwiązania tego rodzaju po praz pierwszy opisał Poncelet (1839). A jak wygląda opór inercjalny w praktyce eksperymentalnej?
Na przykład: jak grunt lub piasek hamuje wpadający niemiecki pocisk? To pytanie postawili sobie, a może raczej postawił rząd Francji inżynierom z miasta Metz niedaleko granicy z Saarlandią. W XIX w. potrzeba była bardzo praktyczna -- związana z przygotowaniami odpowiedniej grubości wałów ziemnych i bunkrów do kolejnych wojen z sąsiadem. Wyniki eksperymentalne potwierdzające sensowność i praktyczną przydatność modelu z oporem typu: Aσ0 + Cd A ρ v2/2, łącznie z rozwiązaniem danym równ. (14b) opisano w encyklopedii amerykańskiej (Johnson's Universal Cyclopedia, 1875 i 1884).
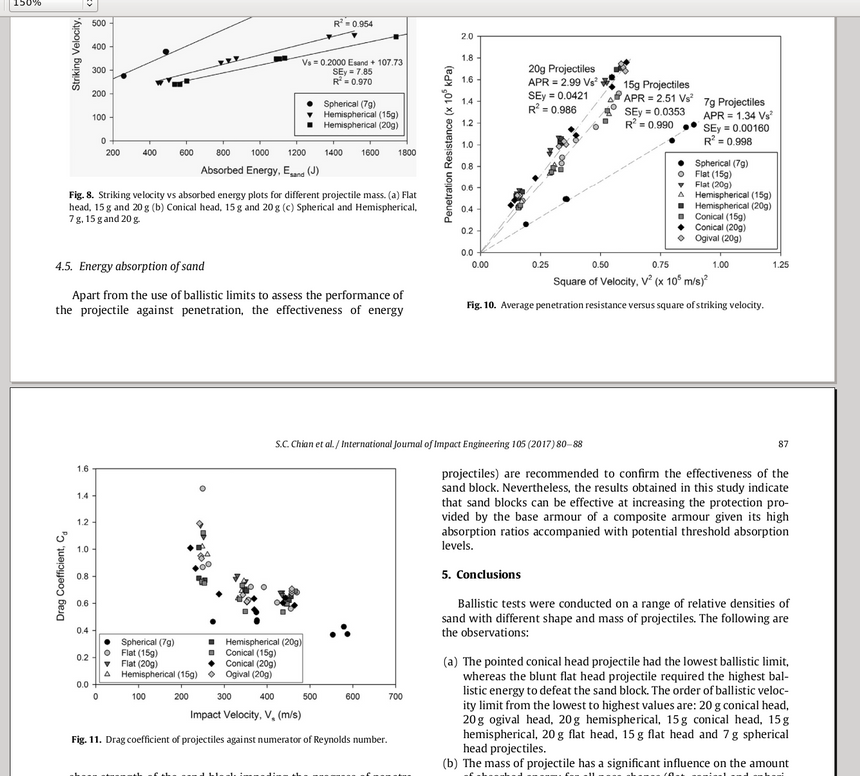
Świeższe dane podaje artykuł "Penetracja pocisków w piasek" Chian, Tan i Sarma (2017), z którego fragment zamieszczam poniżej. Na wykresie 10, średnia siła oporu przy wbijaniu jest skorelowana liniowo (dla kilku różnych typów i kształtów pocisków, co było przedmiotem badań) z kwadratem prędkości pocisku. Na rys. 11 wyliczone z naszego wzoru (11) współczynniki oporu Cd mają oczekiwaną wartość rzędu jedności (od 0.4 do 1.2, z jednym rzadkim wyjątkiem: Cd=1.5).
Ważna jest też zalinkowana w bibliografii praca Omidvara, Malloche, Blessa i Iskandera (2015) w Międzynar. Żurnalu Inżynierii Zderzeń. Traktuje o fenomenologii szybkiej penetracji granularnej ziemi przez pociski. Zakres prędkości wynosił 70 do 300 m/s. Zbadano wiele rodzajów piasków i okruchów kwarcowych o różnych gęstościach (1300 do 1850 kg/m3), średnicach ziaren i wilgotnościach. Wyniki można podsumować tak: mimo, iż zauważa się różnice pomiędzy historiami spowolnienia obiektów wpadających do różnych mediów granularnych, to model inercjalny (~v2) daje poprawną interpretację eksperymentów. Wyznaczone współczynniki Cd równały się jednak 2...6. To bardzo duży zakres i duże wartości Cd; może liczba Reynoldsa kilkucentymetrowych cylindrów stanowiących pociski była na tyle mała, że występowała też składowa lepkości Stokesa (~v) która wzmacniała opór, lecz nie była modelowana, co efektywnie zawyżało Cd. Po wpadnięciu w piaszczystą glebę, pociski zaopatrzone w mierniki naprężeń poddane są wielkiemu pikowi siły oporu dynamicznego, a dopiero po znacznym wyhamowaniu opór dynamiczny zanika i przechodzi w niemal stały opór plastyczny Aσ0, dający stałe przyspieszenie (A/M)σ0. Przykład analizy kilku rodzajów luźnego (panele c,e) i gęstego piasku (panele d,f) podaje rysunek:
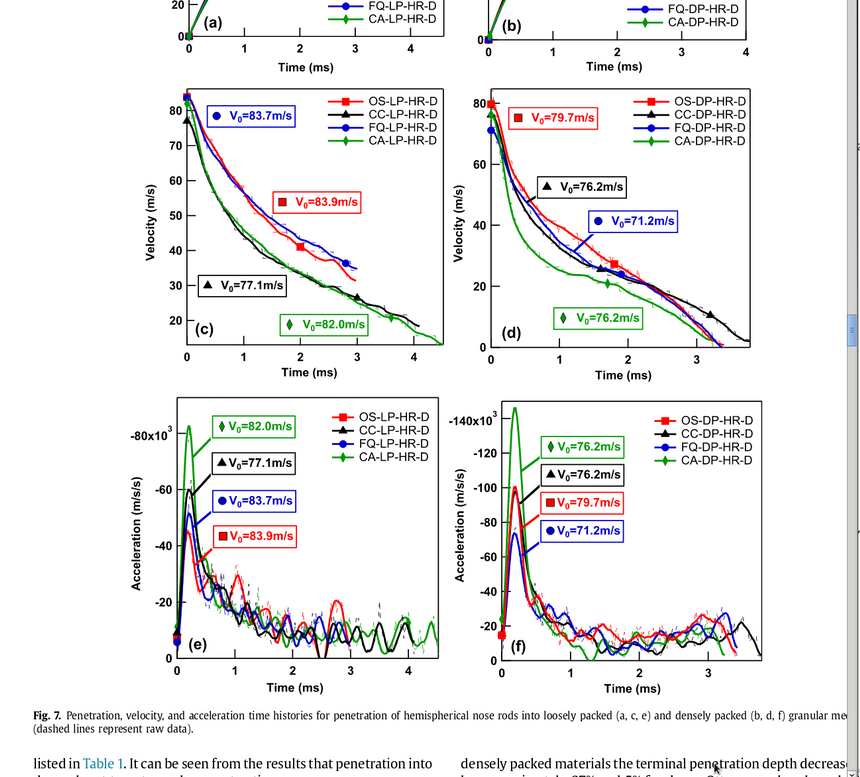
Jak widać na wykresie przyspieszeń w funkcji czasu, maksymalne przyspieszenia dynamiczne (inercjalne) próbników sięgały w niektórych eksperymentach wartości 100e3 do 140e3 m/s2 ~ 10000 g do 14000 g, podczas gdy po spadku prędkości do około 30 m/s działał już tylko opór deformacji plastycznej dający przyspieszenie ~ 104 m/s2 ~ 1000 g. Pominięcie przyspieszenia dynamicznego byłoby więc grubym błędem w modelowaniu sił oporu. A ewentualne pominięcie zależności od głębokości?
Niekiedy opór plastyczny wolno rósł o 50-100% na końcowym etapie procesu, w miarę zanurzania się pocisku/próbnika na większą głębokość s. Autorzy udowodnili, że ten efekt to wynik zależności σ od s, porównując historie zderzeń o dużej prędkości i pomiarów quasi-statycznych, w których wciskano próbniki w materiał z bliską zeru prędkością na głębokość s. W obu przypadkach zauważono mniej więcej liniowy, powolny wzrost oporu statycznego z głębokością, co poprawnie oddaje nasza funkcja g(s) w równaniu (5). Wiele innych przykładów szczegółowych pomiarów, jak i teorii szybkiego wbijania w ziemię zawiera książka Iskandera i in. (2015).
67.4. PODSUMOWANIE CZ. 1
Doszliśmy do dobrego momentu, by podsumować na podstawie omówionej literatury przedmiotu wymagane minimum powagi przy modelowaniu wbijania przedmiotów z dużą prędkością w ziemię:
- Nie warto zagłębiać się w detaliczne modelowanie cyfrowe, jeśli nie jest się pewnym lub nie rozumie fizyki procesu. W szczególności, trzeba wiedzieć jakie są ograniczenia stosowalności modeli gleby (soil) w elastoplastycznych modelach materiałowych gruntu w programie LS-Dyna
- Modele analityczne parametryzujące zjawiska fizyczne są do dzisiaj preferowane w inżynieryjnej analizie eksperymentów dotyczących wbijania przedmiotów w gęste ośrodki
- Siły oporu zależą wielomianowo od zerowej, pierwszej i drugiej potęgi prędkości chwilowej. W zależności od prędkości wbijania, trzeba uwzględniać różne z tych 3 składowych naprężeń. Przy postulowanej prędkości 100-150 m/s, należy zawsze uwzględniać dwie, albo wszystkie trzy składowe, odpowiadające kolejno: naprężeniom deformacji plastycznych, deformacji ścinających typu lepkości Stokesa, oraz efektów inercyjnych (naprężeń dynamicznych kwadratowych w prędkości) opisanych po raz pierwszy przez I. Newtona. Deformacje elastyczne mają zaniedbywalny wpływ na wbijanie.
- Dla lepszej wierności modelu, należy uwzględnić zmianę quasi-statycznego naprężenia plastycznego z głębokością pod ziemią i porównać wyniki z przypadkiem stałej siły oporu plastycznego.
- Parametry swobodne modelu należy ustalić dopasowując je do danych z realnych eksperymentów, prowadzonych we właściwym zakresie prędkości, w tym przypadku od dziesiątek do setek metrów na sekundę.
Te wymagania jakościowe zaniedbano przy próbach wsparcia projektu politycznego Antoniego Macierewicza w podkomisji i na uniwersytecie stanowym w Wichita, Kansas. I to mimo, iż wielokrotnie rozmawiałem z wykonawcami tej pracy zleconej przez Biniendę i Macierewicza. Na ich zaproszenie odwiedziłem laboratorium NIAR po to, by przekazać moje uwagi o projekcie; przekonywałem tam m.in. o konieczności właściwego modelowania gruntu Gerardo Olivaresa.
O kalibracji parametrów modelu analitycznego, poprawnych wynikach, i ich ilościowym porównaniu z nieudanymi symulacjami LS-Dyna traktować będzie druga część tego rozdziału.
(c) P. Artymowicz, 7 wrz. 2020 r.
67.5. BIBLIOGRAFIA
S. Chian, B. Tan, A. Sarma, "Projectile penetration into sand: Relative density of sand and projectile nose shape and mass", Intern. Journal of Impact Engineering 105 (2017) 80-88.
K. Fleming, A. Weltman, M. Randolph, K. Elson, "Piling Engineering, 3rd edition", Taylor & Francis (2009), str. 338
M. Hussein. F. Rausche, G. Likins, "Dynamics of pile driving as a function of ram drop height", in Application of Stress-Wave Theory to Piles (1992, Balkema, Rotterdam)
M. Iskander, S. Bless, M. Omidvar, "Rapid penetration into granula media: Visualizing the fundamental physics of rapid earth penetration", Elsevier (2015)
LS-Dyna "Material selector for LS-DYNA Last updated to dev User's Manual on April 9th 2019" http://www.lstc.com/dynamat/
E. Smith, "Pile driving analysis by the wave equation", ASCE J. Soil Mech. and Found. Div., 86(SM4): 35–61. (1960)
J. Poncelet, "Introduction Ii la Mecanique Industrielle",. Meline, Cans et compagnie, Brussels, (1839)













Komentarze
Pokaż komentarze (61)