Nieudana pętla mjr. Krakowiana - niebezpieczeństwo pętli niekołowych

PĘTLA KOŁOWA

W poprzednim blogu: https://www.salon24.pl/u/fizyka-smolenska/1460796,nieudana-petla-macieja-krakowiana-rekonstrukcja-fizyczna, przedstawiłem analizę pętli kołowych takich, jak ta poniżej (q=0). 

Rys. 1. Pętla kołowa F-16 ze stałym ciągiem. Link do rys. 1

Samolot wchodzi do pętli z lewej strony na wysokości 30 m nad ziemią. Ma na dole pętli prędkość 344 kt (177 m/s, albo 637 km/h). Natychmiast pilot jest poddany obciążeniu (niektórzy mówią przeciążeniu) 5.66 g. Przypominam, że piloci wojskowi trenują wytrzymałość na przeciążenia do 9 g. 

Wszystkie późniejsze dane są podane na rysunku co sekundę lotu. Czarne liczby to czynnik obciążenia w jednostach g. Pomarańczowe liczby to prędkość przeciągnięcia w węzłach. Musi być zawsze mniejsza niż niebieska liczba nad nią, pokazująca chwilową prędkość samolotu względem powietrza, w tych samych jednostkach. Jak łatwo zauważyć, kołowa pętla w F-16 nie niesie żadnego niebezpieczenstwa przeciągnięcia. Jeśli jednak ciąg jest duży i stały, jak w tym przykładzie (9.5 ~ 10 ton siły), to po przeleceniu górki pętli z dodatnim obciążeniem 1.37 g, samolot rozpędza się i dla utrzymania kołowej trajektorii na części opadającej trajektorii wynagane jest większe przeciążenie. W 4-tym kwadrancie pętli dochodzi do największego n = 7.28, gdy kąt pozycyjny samolotu wynosi 344^o a prędkość 400 kt. Przeciążenie od tego punktu nieznacznie maleje do końca pętli, która trwa 27.5 s ~ 28 s. Promień pętli, 686 m jest stały, dając średnicę 4500 ft. Gdyby pętla była prawie kołowa, nie byłoby zatem problemu. 

Major Krakowian nie zamierzał jednak utrzymać idealnie kołowego kształtu pętli!   

TEORIA  PĘTLI NIEKOŁOWEJ 

W Radomiu pętla była zdeformowanym okręgiem, wypłaszczonym na górze/dole i na mniej więcej pionowych częściach trajektorii. Zaś pomiędzy tymi odcinkami, na czterech 'rogach', trajektoria była bardziej zagięta, niż kołowa.

Przyjmę następujący model matematyczny kształtu pętli. Niech r(φ) będzie zmienną wraz z kątem pozycyjnym φ = 0...2π odległością punktu na krzywej od środka pętli (ten punkt  zilustruję czerwonym krzyżykiem). Pozostawiamy początkowy promień  r(0) = R₀ = 2250 ft niezmieniony. Wprowadzamy bezwymiarowy parametr niekołowości 0 < q < 0.2 (zero daje okrąg, 0.2 to już zaokrąglony kwadrat, nie okrąg): 

 r(φ) =  R₀ (1 + q  sin² 2φ)                                                                                                                          (1) 

Teoria ruchu z małym parametrem q, ze stałym lub zmiennym ciągięm i omówionym w poprzednim odcinku bloga oporem aerodynamicznym zleżnym liniowo od przeciążenia a kwadratowo od prędkości, jest dość prosta. Choć trajektoria r(φ) jest podana jako funkcja kąta pozycyjnego φ,  to ułożymy równanie na zmienność prędkości w czasie (zmienna t). W odróżnieniu od przypadku kołowego, odległość ds przebywana przez samolot w czasie dt odpowiadającym przyrostowi kąta dφ nie jest równa R₀ dφ, zależy teraz też od φ, gdyż trajektoria nie jest na ogół prostopadła do promienia wkazującego położenie samolotu. Wiedza o ds będzie nam potrzebna. Powiązać ds z dφ można przy pomocy twierdzenia Pitagorasa i równania (1), 

ds/dφ = [r² + (dr/dφ)²]^1/2  = R₀ [(1 + q sin² 2φ)²  + (2 q  sin 4φ)²]^1/2                                                  (2)

Zmienia się w czasie ruchu nie tylko prędkość v = ds/dt = (ds/dφ) (dφ/dt), ale także krzywizna trajektorii. A przyspieszenie odśrodkowe to kwadrat prędkości podzielny przez właśnie promień krzywizny. Wyrażenie na chwilowy promień krzywizny r_c  jest odwrotnością matematycznie zdefiniowanej krzywizny κ (zob. ten artykuł, tylko popraw parę pomyłek, np. w formule na κ potęga równa jest 3/2, a nie 1/2, co ujawnia analiza wymiarowa). 

r_c  = (ds/dφ)³  / [2 (dr/dφ)²  – r (d²r/dφ²)  +r²]                                                                                       (3)

gdzie z równania (1) mamy

dr/dφ = 2 q R₀ sin 4φ, 

d²r/dφ² = 8 q R₀ cos 4φ. 

Czynnik obciążenia n, potrzebny do wyliczenia chwilowej wartości oporu czołowego, wynosi 

n = v²/r_c + cos φ. 

Przeciążenia zależą silnie od promienia r_c, którego wartość nawet przy niewielkim parametrze niekołowości q ~ 0.075 jest zaskakująco różna od R₀. W modelach zaprezentowanych niżej, w trakcie pętli promień krzywizny może być (na przemian cztery razy) równy 2.4 R₀, a wkrótce potem 0.64 R₀. Prędkość v nie zmienia się szybko, więc mamy silne, lokalne zmiany przeciążenia wywołane niekołowością. 

Zasadnicze, zwyczajne równanie różniczkowe, które całkujemy numerycznie dwukrotnie po czasie by otrzymać v(t), a stąd φ(t) i r(t), sumuje wkłady od ciągu T, grawitacji ziemskiej g, i oporu powietrza, i mówi jakie jest chwilowe przyspieszenie samolotu o masie M=15000 kg wzdłuż trajektori ruchu: 

dv/dt =  T/M – g sin φ   –  [(4+n)/5] (D₀ /M) (v/v₀)²                                                                                    (4)

gdzie D₀ = C_d0 A ρ_air v₀² /2  ma omówione już w pierwszym blogu znaczenie, tyle że zmieniam tu odrobinę wartość gęstości powietrza na ρ=1.22 kg/m³ dla uwzględnienia ciepłego dnia w Radomiu.

WYNIKI:  MODELE ZE STAŁYM CIĄGIEM i parametrem kształtu pętli q  =  0.06 oraz  0.075

Okazuje się, że nawet niewielka wartość parametru q = 0.06 zapewnia dobrze widoczną na rysunku 2 niekołowość pętli. 

Rys. 2.   Model ruchu F-16 w niekołowej pętli. Na czerwono zaznaczono powierzchnię ziemi. Zielony okrąg podany jest dla porównania. Czynnik przeciążenia n podany jest dużymi czarnymi liczbami w punktach trajektorii oddalonych o 1 sekundę. (Link do oryginału)  

W ruchu po pokazanej krzywej, przeciągnięcia nie zagrażają: por. niebieskie i pomarańczowe liczby węzłów odpowiednio: v i v_S. Tam, gdzie spada prędkość, spada też z pierwiastkiem kwadratowym  n^1/2 prędkość przeciągnięcia v_S.  Ta górce pętli jest ciągle dodatnie obciążenie, ale tym razem małe: w minimum  to 0.28 g. 

Na wypłaszczonych odcinkach trajektorii niedaleko φ = 0, 90, 180, 270 stopni, przeciążenia są mniejsze od widzianych w pętli kołowej (q=0). Odwrotnie przy φ ~ 45, 135, 225 i 315 stopni. Najgroźniejsze jest to naturalnie przy tym ostatnim kącie, gdzie samolot pikuje jeszcze w dół, choć już w pozycji normalnej, nie odwróconej. Tam obciążenie pilota jest przez krótki czas (1s) pozakrytyczne, a system fly-by-wire F-16 prawdopodobnie ingerowałby i nie dopuścił do n > 9, czyli ponad 9 g. Efektem akcji ogranicznika systemu sterowania byłaby inna niż planowana, niezamknięta trajektoria, być może przecinająca ziemię, ale w tym konkretnym przypadku małej niekołowości trzebaby to sprawdzić..

Zobaczmy  trajektorię z parametrem q=0.075, wyraźniej niekołową. Przypomina ona wg mnie lepiej pętlę radomską. 

Rys. 3. Niekołowa pętla zbliżona do widzianej w Radomiu 28.08.2025. (Link.) Parametr niekołowości  q=0.075. Symbole jak na rys.2. Pętla wykonywana w F-16 przy takich założeniach (stały ciąg, bardzo niski start nad ziemią, niekołowość) nie może zakończyć się szczęśliwie. Przez krytyczne 1.4s na wys. poniżej ~300 m nad ziemią, przeciążenie przekracza maksymalne dozwolone dla samolotu F-16 bez dodatkowych baków konformalnych 9 g (samolt w Radomiu takie baki miał, co nie pomaga w akrobacji lotniczej). Do tego dochodzi niebezpieczeństwo utraty przytomności pilota. Wynikiem próby wykonania takiej pętli jest nieuchronny CFIT. 

Czas trwania nadkrytycznych przeciążeń (ponad 9 g) wydłużył się w por. z rys. 2 z 1s do 1.4 sekundy, a wartość maksymalna wyniosła 10 g (pomiędzy punktami n = 9.41 i 9.68). Jak mówiłem, do tego automatyka raczej nie dopuści i rezultatem będzie mniej ciasna końcówka pętli zakończona CFIT-em. Ta konkretna pętla jest więc zabójcza, głównie dlatego, że zaczęta jest na zbyt niskiej wysokości. Widzimy tu dlaczego nie należy próbować, startując nisko nad ziemią, utrzymywać dużego ciągu silników. 

DODANY  NA  SZCZYCIE  PĘTLI  ODCINEK LOTU  POZIOMEGO 

Wydaje się, że mjr Krakowiak dodał do pętli krótki odcinek lotu poziomego na szczycie. Zobaczmy jak przy założeniu lotu przez Δt = 2s zmienia się dynamika lotu, przy uwzględnieniu że musimy skrócić czas pętli sensu stricto z 28s do do 26s.

W  modelu biorę pod uwagę zmianę prędkości samolotu na dodanym odcinku. Zakładam, że wpółczynnik oporu powietrza w locie odwróconym F-16 (n=–1) jest ten sam, co w locie normalnym (n=1). To pozwala samolotowi rozpędzić się o najwyżej o kilka  m/s, co nie stanowi jakościowej zmiany. Ważniejsze że pętla bez płaskiego odcinka trwa 26s a nie 28s.

Z wymaganego krótszego czasu pętli wynika, że pilot mógł planować następującą pętlę z dodaną płaską górką:

wysokość pętli 2R₀ ~  4000 ft,   prędkość początkowa  v₀ = 310 kt .

Te okrągłe, łatwe do zapamiętania liczby, miałyby przy treningu wielki sens. Taką pętlę rzeczywiście samolot mógłby wykonać na stałym ciągu 93.2 kN (9.5 tony) w czasie 26s, osiągając na szczycie stan nieważkości, z którego latwo przejść od razu do lotu odwróconego z n=–1.  Jedyny problem to, jak już wiemy, przeciążenia pod koniec pętli:

Rys. 4. Znak \\ rozrwanej pętli na górze symbolizuje, że modelowana jest pętla z dodanym tam, lecz nie wykreślonym, odcinkiem 2 sekund lotu odwróconego, poziomego, na drodze 244 m. Cała lewa strona rysunku powinna być przesunięta o tę odległość w lewo. W tej pętli przeciążenia dochodzą chwilowo do 11 g, co prowadzi do CFIT-u.  Link do rys. 

JAK  MOŻNA  ZROBIĆ   BEZPIECZNĄ   PĘTLĘ   NIEKOŁOWĄ

Widzieliśmy kilka przykładów niekołowych, niebezpiecznych pętli kończących się CFIT-em (Controlled Flight Into Terrain). 

Metodą zapobiegania takim wypadkom jest nie wydawanie pozwoleń na bardzo niskie manewry na pokazach lotniczych, a w lotach treningowych - zakaz inicjacji pętli poniżej 1000 ft AGL (chandelle, beczki, ósemki kubańskie i inne manwery nie są tak niebezpieczne, choć split-S jest szalenie niebezpieczny i nie należy go próbować myśliwcem z wys. poniżej 5000 ft AGL). 

Czy jest jakiś ratunek dla F-16 który zaczął pętlę za nisko? Oczywiście jest. Jak to opisywałem poprzednio, nawet jeśli mielibyśmy start z niebezpiecznie małej wysokości 30 m, i planujemy lub z innych powodów wykonujemy niekołową pętlę, wystarczy albo:

(i) przerwać pętlę i zrobić półbeczkę w pierwszej połowie trzeciego kwadrantu trajektorii (φ pomiędzy 180 a 225 stopni); wówczas wejdziemy w ósemkę kubańską, gdzie opadamy pod kątem 45 stopni do horyzontu, figura stanie się bezpieczna. 

albo 

(ii) kontynuować  pętlę na znacznie (pon. 2x) zredukowanym ciągu silnika: wyłączyć dopalacz i zmniejszyć częścowo throttle.

Oto dowody obliczeniowe.

Przyjmuję, że zrobiono (ii) i zredukowano ciąg w czasie 1s, z 10 do 4 ton siły w przypadku bez lotu poziomego na górze: 

Rys. 5 (Link do wykresu). Niekołowa pętla wykonywana z redukcją ciągu z 10 do 4 ton, na drugiej części trajektorii pokazanej cienką niebieską linią. Odjęcie ciągu na górze pętli powoduje, że przeciążenia pod jej koniec są normatywne (< 9 g). Cienka niebieska linia znaczy zmniejszony ciag), zielona - okrag, dla porównania.

Natomiast w przypadku gdy figura zawiera dodany okres 2 sekund i 255 metrów przebytych na stałej wysokości na szczycie pętli, mamy ten model, również nie powodujący nadmiarowych przeciążeń ani wypadku: 

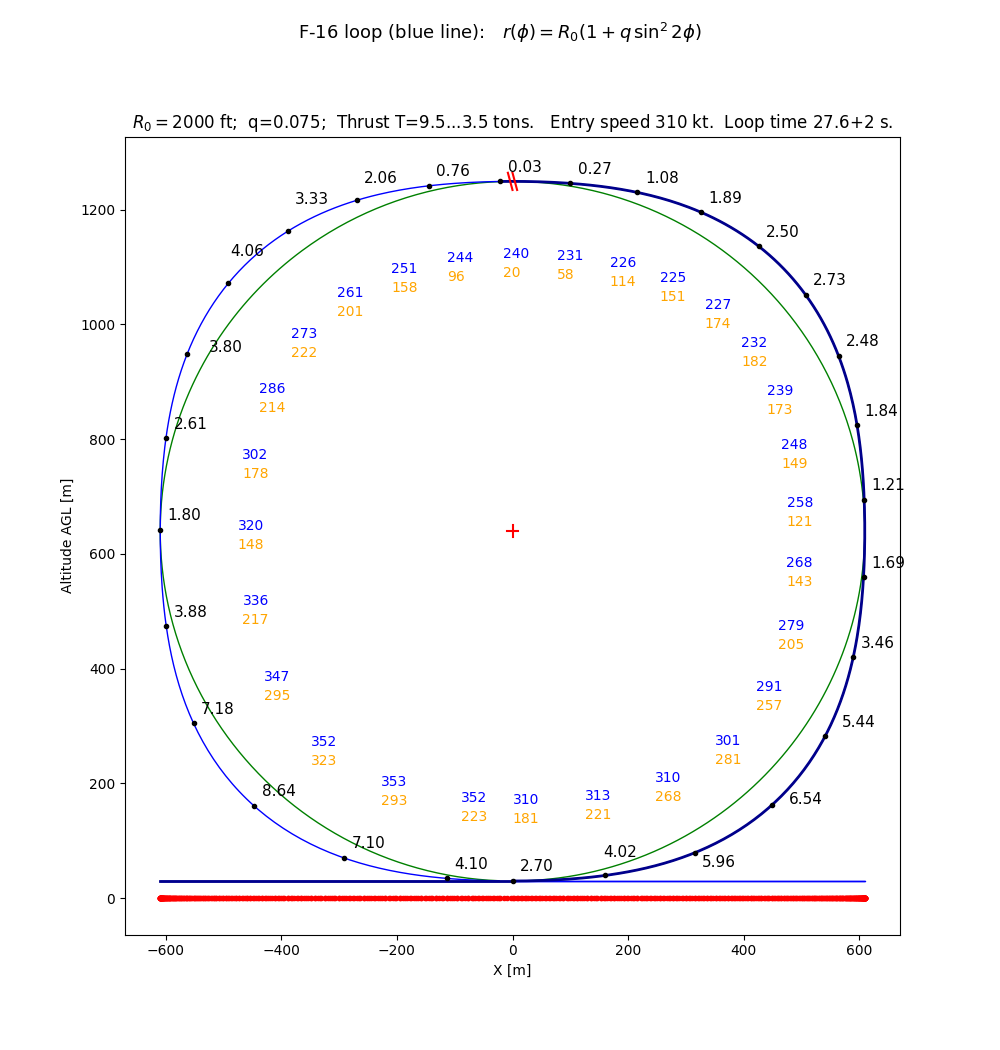
Rys. 6. Pętla z rys. 5 robiona z redukcją ciągu z 9.5 do 3.2 tony, następującą po 2s poziomego lotu odwróconego na odcinku 255 m (nie pokazanego, lecz zaznaczonego kreskami \\). Ta pętla może zostać wykonana, ponieważ przeciążenia są < 9 g, i nie dochodzi do przeciągnięcia. Link do rysunku. 

Redukcja ciągu zmniejsza na tyle prędkość opadania, że nie występują nadnormatywne przeciążenia, g-lock, nie ingeruje automatyka samolotu, nie następuje też przeciągnięcie, choć w czasie najwyższego przeciążenia na rys. 6, prędkość samolotu nie przekracza  pr. przeciągnięcia o więcej niż 10%.  

Żadna z omówionych dwóch metod nie uratuje nas w groźnej sytuacji, jeśli nie rozpoznamy problemu z niekołową pętlą najpóźniej w trzecim jej kwadrancie, i samolot będzie już pikował pod kątem większym niż ~60^o do horyzontu, w pozycji odwróconej lub normalnej. Wtedy dojdzie do wypadku, niezależnie od jakichkolwiek (spóźnionych) działań pilota. 

* * * 

Mam nadzieję, że wyjaśniłem sobie i Wam zasadnicze przyczyny wypadku ś.p. majora Macieja Krakowiana. Naturalnie, może PKBWL LP po zbadaniu rejestratorów i tego co zostało z F-16, ujawni jakieś szczegóły różniące się od schematu CFIT-u tu zaprezentowanego. Zaczekamy na raport wstępny. Do tego czasu, nie róbmy żadnym samolotem pętli z niebezpiecznie małej wysokości (a 30 m jest zawsze niebezpieczne w przypadku pętli), zwłaszcza na dużym ciągu w czasie opadania - margines błędu jest wtedy bardzo bardzo mały i znika gdy nie utrzymujemy kołowego kształtu pętli. 

(c) P. Artymowicz - dn. 8 wrz. 2025 r.

PS.  Program w Pythonie liczący model z  rys.3. jest tutaj, a z rys. 5 tutaj.  Model z odcinkiem 2s lotu poziomego na szczycie pętli jest lioczony przez ten program.