W rozdz. 15 opisałem prostą teorię przybliżającą lot końcówki skrzydła jako ruch w dwóch myślowo wyodrębnionych fazach. Początkowo jest to silnie przyspieszony ruch środka masy, w wyniku siły nośnej skrzydła (zamiast 'koncowki skrzydla' bede tu pisac 'skrzydla') z jednoczesnym rozkrecaniem obrotu wokół długiej osi. W tej fazie, przednia krawędź natarcia podnosi się do góry i w ułamku sekundy (t1, standardowo t1=0.17 s) stawia skrzydło prostopadle do kierunku lotu. W tej krótkiej fazie ruchu siła nośna maleje do zera ze względu na rosnące pochylenie (pitch), a współczynnik siły oporu zmienia się (rośnie lub maleje) od początkowej wartości Cd=0.18 odpowiadajacej sytuacji skrzydła przed oderwaniem, do założonej wartości końcowej podanej na rysunku.
W drugiej fazie, obrót jest kontynuowany jako mniej wiecej ustalony, a w każdym razie szybki. Wcześniej podałem rząd wielkości: ~3 pełne obroty na sekundę. Tutaj uścislę nieco te wielkości. To wielkość osiągana od początkowego aż do pionowego ustawienia skrzydła, jednak kiedy skrzydło leci przy AOA = 90...180 stopni, wtedy obrót jest hamowany. Dlatego prędkość kątowa oscyluje pomiedzy tą największą, ~3 obr/sek, a pewną znacznie mniejszą, osiaganą "pod wiatr" (AOA ~ 0 lub 180 stopni). Można więc przyjąć, że obraca się ze średnią predkością kątową ~1.5 obr./sek i robi na całej swej drodze ~5 pełnych obrotów, co zostało zobrazowane symbolicznie na rysunkach. Dodatkowo, prędkość kątowa może maleć, kiedy spada predkość postępowa. Skrzydło musi obracajac się bowiem zawsze spełniając warunek
omega*r << V,
gdzie omega jest pr. katowa, r jest połową rozpietości profilu (r~1 m = srednia polowkowa szerokosc skrzydla), a V jest zmienna w czasie predkoscia postepowa. Krawedz obracajacego sie skrzydla znajdujaca sie dokladnie nad lub pod srodkiem jego masy nie moze lecic z predkoscia (V+- omega*r) znacznie rozna od V, gdyz taki ruch bylby szybko tlumiony przez pare nierownych sil na koncach profilu. Poczatkowo ta nierownosc jest niezle spelniona, gdyz r*omega < (1 m) * (3*2pi/sek.) ~18 m/s, zas V = 77 m/s. Pozniej jest ona spelniona, poniewaz zarowno omega jak i V maleja w czasie. Nadal jednak oczekuje, ze skrzydlo obroci sie wiele razy w ciagu swej drogi. Ile razy, a zwlaszcza w jakiej pozycji katowej uderzy w przeszkode, trudno bedzie obliczyc jednoznacznie, nawet w numerycznych obliczeniach gazodynamicznych. Prosze nie traktowac katow pochylenia ladujacego, koziolkujacego wczesniej skrzydla jako obliczonych lub znanych, beda zilustrowane graficznie arbitralnie.
Dochodza tez skladowe obrotu wzdluz pozostalych dwoch osi, ale najszybszy jest wlasnie obrot wokol najdluzszej osi niesymetrycznego skrzydla. Mozna bowiem podac analogiczne ograniczenia na szybkosc obrotu wokol tych osi, omega*r<<V, dla ktorych r >1 m, a wiec obrot jest wolniejszy. Sila nosna dziala raz w dol raz w gore, przez co srednio kasuje sie, a opor ruchu opisany jest usrednionym po czasie (albo po obrocie) wspolczynnikiem Cd, przybierajacym wartosc okolo 0.8, tzn. zblizona bardziej do maksymalnej wartosci Cd=1.2 dla skrzydla ustawionego bokiem do kierunku ruchu, niz do oporu Cd=0.04 (parasitic drag) dla skrzydla tnacego powietrze bokiem i na plasko, nie produkujacego zadnej sily nosnej, a zatem i zadnego oporu indukowanego.
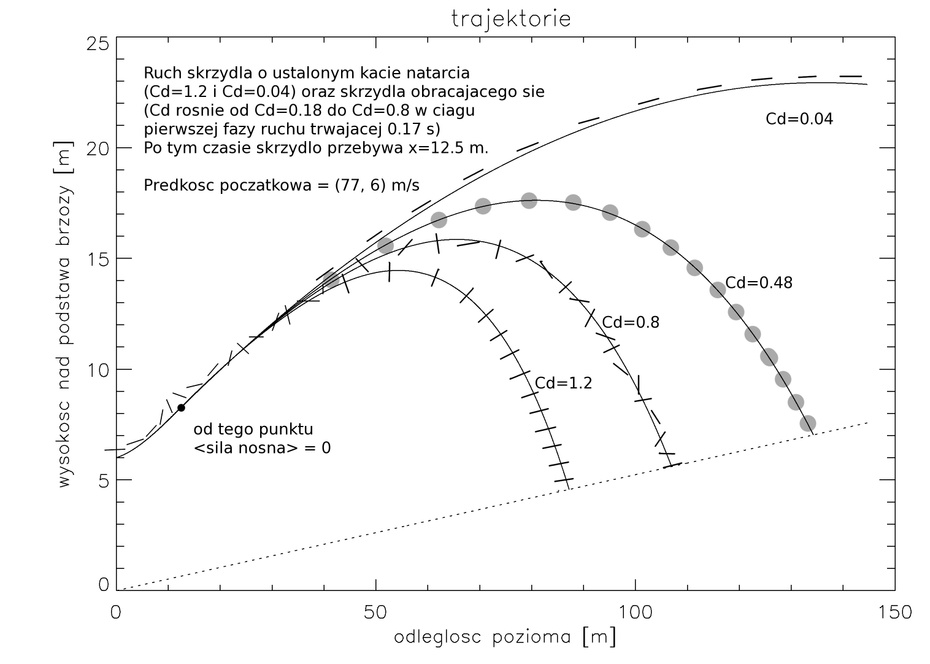
Uzupelnie tutaj te obliczenia rysunkami trajektorii oraz polozenia skrzydla wzgledem jego osi dlugiej. Na osi poziomej jest odleglosc od pnia brzozy w kierunku zachodnim. Linia przerywana zaznaczylem zalozone nachylenie terenu. Polozenia plaszczyzny skrzydla w przestrzeni sa schematyczne, to znaczy dodalem je reka :-|, ale sa zgodne z obliczonymi badz zalozonymi danymi o obrocie. Odstepy, w jakich rysowalem polozenia oddaja dynamike ruchu, ale tylko w jakosciowy sposob. (Nie przylozylem sie, jak to teraz widze, do tego aspektu krzywej Cd=0.04. Inne krzywe sa realityczne pod tym wzgledem.) Czarna kropka w odleglosci 0 m do 13 m za brzoza zaznacza koniec 1-szej fazy ruchu.
Przypadek Cd=0.48 to kula o stosunku pola powierzchni przekroju do masy takiej samej jak skrzydlo (pokazane dla porownania; kula stawia dosc duzy opor aerodynamiczny, ale mniejszy niz koziolkujace skrzydlo; nie traktuje jej tu powaznie, wiec czasami dostaje ona poczatkowa sile nosna, choc nie powinna).
OBLICZENIE STANDARDOWE
Na pierwszym rysunku u gory widac najlepszy model ruchu koziolkujacego skrzydla (Cd=0.8). Startujac (podobnie jak wszystkie obliczenia na tym rys.) z predkoscia poczatkowa 77 m/s w poziomie (jak w obliczeniach zespolu Biniendy) ale znacznie bardziej realistycznie vz= +6 m/s pionowo w gore, koziolkujace skrzydlo konczy lot w odleglosci x = 107 m za brzoza. (Jest to obliczenie zaniedbujace zboczenie w prawo wzdluz osi y, ktore jest male w porownaniu z ta odlegloscia i nie wplywa zasadniczo na zasieg lotu.)
Innym poprawnym, jak mi sie wydaje (zgodnym ze sladami na ziemi) wynikiem moich prostych obliczen jest kat padania skrzydla na ziemie, odrobine bardziej rozwarty niz 30 stopni wzgl. terenu (por. dH/dx na rysunku, gdzie H to wysokosc nad terenem). Czy to jest ok? Koncowka wg. mojego modelu nie leciala w przyblizeniu poziomo, tylko wzniosla sie ponad zarosla, czesciowo dzieki temu chwilowemu kopniakowi od sily nosnej. Gdyby leciala bardziej plasko, poscinalaby galezie ktore byly tam nietkniete i sama by doznala duzych uszkodzen. Ostatnio blogger Tommy Lee staral sie wyznaczyc kat padania koncowki skrzydla w zarosla, ale zamiast tego niechcacy wyznaczyl (i to bez poprawnego uwzglednienia perspektywy i trojwymiarowosci sytuacji; jego wynik to 53 stopnie wzgl. horyzontu) kat padania skrzydla na sam grunt, po uderzeniu w galezie. Poniewaz galezie wiszace nad ziemia nosily na zdjeciach wyrazne slady uszkodzen, a wiec hamowania na nich skrzydla, kat padania na glebe nie byl katem lotu. Interesujacego nas kata nie wolno mierzyc od poziomu terenu, tylko od poziomu pierwszych urwanych galezi. Nie mamy jeszcze zadnych danych na jeg temat.
Jak widac na pierwszym rysunku, gdyby skrzydlo magicznie ustawialo sie ciagle w kierunku lotu lub w poprzek tego kierunku, stawialoby minimalny/maksymalny opor aerodynamiczny i przelecialoby x >> 150 m, wzglednie x ~ 90 m.
Gdyby rozkrecanie pokazanego schematycznie kreskami obrotu skrzydla trwalo polowe obliczonego w rozdz. 15 czasu, czyli gdyby t1 = 0.085 s, wtedy koziolkujace skrzydlo wyladowaloby x = 90 m od brzozy. Nie zalaczam osobnego rysunku. Gdyby zas od razu krecilo sie kilka razy na sekunde (t1=0), wtedy przelecialoby 80 m. Z drugiej strony, jesli moment sily zadzierajacy krawedz natarcia ku gorze byl mniejszy i wyniku tego t1 = 0.25 s, wtedy skrzydlo dolecialoby az do x = 120 m. To jest mozliwy wynik prostego modelu, trzeba pamietac o nieoznaczonosci: zasieg wynosil z tego co powiedzialem wyzej, (107 +13 -17) m i jest spojny z miejscem upadku skrzydla.
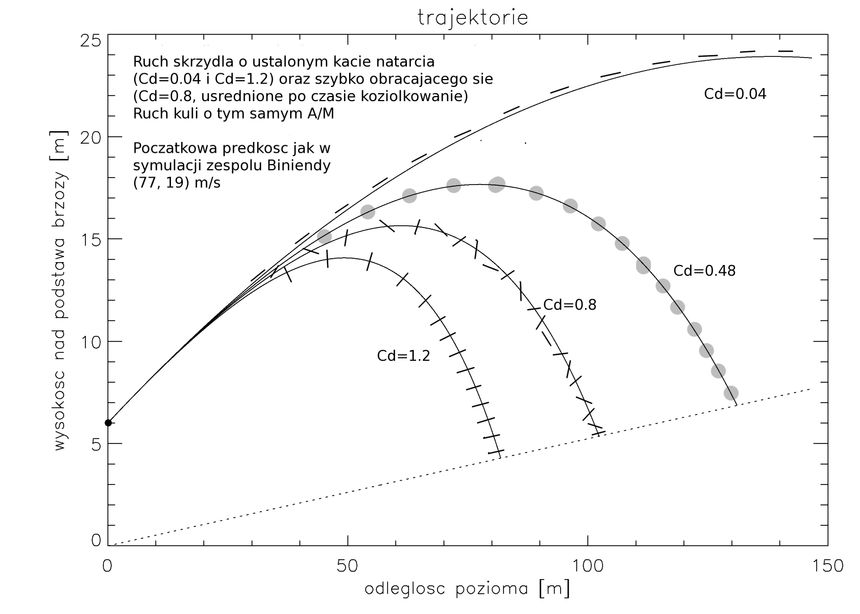
WARIANT Z DUZĄ POCZĄTKOWĄ PREDKOSCIĄ PIONOWĄ
Rysunek drugi pokazuje wariant obliczen, ktory zaklada ze poczatkowa predkosc pionowa rowna jest az +19.2 m/s, podobnie jak w obliczeniach zaprezentowanych przez zespol Biniendy. W tym wariancie, zaniedbuje sie faze pierwsza, poniewaz jedyna fizyczna interpretacja takiego warunku poczatkowego (+19 m/s, co odpowiada doslownie skrzydlu wylatujacemu spod ziemi) jest to, ze jest to wlasnie koncowa predkosc pionowa uzyskaana na etapie pierwszego cwierc-obrotu skrzydla. Jak widac, taki balistyczny model bez sredniej sily nosnej daje podobne odleglosci koncowe co standardowy (pelny).
WARIANT MINIMALIZUJACY ZASIĘG LOTU
Trzeci rysunek to obliczenie wariantowe, w ktorym probuje zmienic parametry maksymalnie w taka strone, zeby skrocic lot skrzydla. Nie jest powiedziane, ze robie rozsadnie, na przyklad wymaga to bowiem skrocenia fazy pierwszej, a nie jest jasne czy bardziej skomplikowane rozwazania niestalego momentu sily zadzierajacego nosek profilu do gory nie powinny dac wrecz przeciwnej zmiany t1 na dluzszy. Ale, jak powiedzialem, chcemy zobaczyc jak blisko, a ciagle w sposob fizyczny, skrzydlo moze doleciec. Druga modyfikacja to znacznie zmniejszosna predkosc poczatkowa skrzydla. Mozna sobie wyobrazic, ze uginajac brzoze przed oderwaniem, cala koncowka skrzydla jest spowalniana jako calosc. Z jakim przyspieszeniem? No coz, konstrukcje samolotow pasazerskich sa obliczone na tego typu przyspieszenia na pewno nie wieksze niz okolo 10g, co odpowiadaloby przyspieszeniu w poblizu miejsca styku z brzoza kika razy wiekszemu. Jednak badzmy super ostrozni i zalozmy na chwile, ze fizycznie dopuszczalne jest przyspieszenie srodka masy koncowki skrzydla rowne a =25g (oszacowanie gorne). Innymi slowy, zakladamy ze do momentu zerwania konstrucji wszystkich dzwigarow, keson w jakis niezbyt jasny sposob wytrzymywal a ~ 25g. Wtedy predkosc skrzydla w momencie zerwania to V = V0 - a*t, gdzie t jest czasem giecia brzozy i spowalniania masy skrzydla, a V0 ~ 77 m/s. Zakladajac a=const (wiem, wiem, ze to wszystko machanie rekami, ale jak bede to robil dokladniej, to dostane wieksza wartosc predkosci poczatkowej skrzydla, a chce tu zabawic sie w wariant dajacy mala odleglosc lotu), mamy
(1/2) |a|*t^2 ~ S,
gdzie S ~ 1.5 m jest realistycznym maksymalnym wychyleniem poziomym brzozy, oraz
V = V0 - sqrt(2 |a| S) ~ 50 m/s.
Jest to V~(2/3) V0, czyli skrzydlo startuje w tym przypadku z energia mniejsza, niz polowa tej, jaka ma w obliczeniu standardowym. Rowniez pionowa predkosc poczatkowa samodzielnego lotu skrzydla jest wzieta jako odpowiednio mniejsza, +3.9 m/s zamiast 6 m/s. Dodatkowo, skrzydlo nie jest wyrzucane do gory przez sile nosna na poczatku swej drogi.
Wyniki tego skrajnie ograniczajacego odleglosc spadku skrzydla, wariantowego obliczenia na rys. 3 sa takie, ze skrzydlo musi przeleciec co najmniej x~67 m za brzoze. (Pamietajmy ze Cd=1.2 to ilustracja geometrii lotu ktora nie jest naprawde mozliwa, ale i ten absolutnie skrajny wariant odpowiada sporej odleglosci x ~ 58 m).
Tak więc, obliczenia wariantowe potwierdzają niemożliwość odległości lotu rzędu x ~ 12 m w kierunku lotniska, co było wynikiem obliczeń numerycznych zespołu ekspertow Macierewicza. Była już o tym mowa w rozdz. 15.
ANALOGIE [dodane 13.12.11]
Jeśli chodzi o obrazowe porównania, to dobre przytoczył jeden z komentatorow w dyskusji poniżej, choć wyciagnal złe wnioski. Dobrym przybliżeniem urwanego skrzydla byłaby dość ciężka maska samochodu BMW 540 jadącego z predkościa 250 km/h, ktora unosi się i otwiera pod wpływem siły nośnej i odrywa od samochodu tak, że wylatuje w górę z prędkoscią kilku metrów na sekundę. Czy maska samochodu (która ma A/M wieksze niż skrzydlo, czyli powinna spaść znacznie bliżej, niż skrzydlo) spadnie po 1/3 sekundy w odległości 2.5 długości pędzacego samochodu, 12 m od miejsca oderwania? Nonsens.
Maska samochodu, slizgacz, samochod , te obiekty poruszajace sie z predkosciami podobnymi do tupolewa, ale nie lecace w gore jak skrzydlo smolenskie w momencie urwania, sa podrywane tak jak opisywalem i przelatuja ponad 50 m robiac jeden-dwa obroty, zanim zejdą do poziomu startowego. W istocie, samochod wyscigowy rozkrecal sie (faza 1; 0.25 obrotu) przez cala sekunde. Miał bowiem większy moment bezwladnosci, a mniejszy moment sily, niz skrzydlo. W ciagu drugiej sekundy zrobił natomiast 1.75 obrotu (faza 2), ten obrot nie dajacy juz sredniej sily nosnej bylby kontynuowany, gdyby tor sie skonczyl i byla dalej przepasc. Pozostawiam wszystkim odpowiedź na pytanie: dlaczego samochod nie uderzyl w ziemie po 1/2 obrotu, a nawet po 1 obrocie? Przecież siły nośne w pozycji poczatkowej i do góry nogami byly przeciwnie skierowane? Dlaczego się nie uśrednily i samochód musiał opaść dopiero w ciągu swojego drugiego obrotu mniej wiecej balistycznie (przy okazji: balistycznie nie oznacza bez oporu, tylko bez sily nośnej, a jedynie z oporem czołowym, jak kula armatnia). Ten rodzaj ruchu opisywalem słowami, zanim dostrzegłem to wideo.
Samochód wyścigowy przelecial w ciągu dwóch sekund ~45 m/s * 2 s, czyli ~90 m, gdyż jego predkości początkowe i końcowe lotu można oszacować jako 200 km/h i 100 km/h. Nie liczylem tego przypadku, ale maska samochodu spadłaby także nie bliżej niż po ~50 m. Uwzgledniając początkowe nachylenie trajektorii, skrzydło powinno zatem dotrzeć zdecydowanie dalej, niz x = 50 m, co też zrobiło.
WZMOCNIENIE WNIOSKU O NIEFIZYCZNOSCI SYMULACJI ZESPOŁU [dodane 18.12.11]
Ostatnio Ford Prefect fajnie przybliżył zakrzywiony odcinek trajektorii w symulacji prof. Biniendy jako okrag o tak malym promieniu, 1.5 m, ze dostal oszacowanie |a|, przyspieszenia na tym odcinku znajdujacym sie jakies 5-6 m za podstawa drzewa, rowne |a| ~ 100 g. Moj nastolatek i ja sadzilismy w powyzszych rozwazaniach, ze to "tylko" 63 g. Dobrze! Wezmy ~100 g! Nasze formuly sa bardzo zbliżone, gdyż i jedna i druga opiera się na dzieleniu prędkości V przez czas ruchu, proporcjonalny do r/V. Stad a ~ V^2/r nie tylko w ruchu kolowym ale i prostoliniowym. My bralismy srednie predkosci V, moze dlatego otrzymalismy mniejsza wartosc. Tak szybko (a~100g) moze hamowac przy predkosci poczatkowej V~ 63 m/s (nie 77 m/s jak na poczatku, bo juz dzialal spory opor aerodynamiczny przed tym wirazem) skrzydlo o prametrach A=const i M=600kg, ustawione prostopadle do wiatru względnego (czyli niemal dokładnie do kierunku ruchu, w tym przypadku), jeśli
A = |a| M /(Cd * 0.5*rho*V^2)
gdzie Cd=1.2 (w przypadku obiektow 3-d to praktyczne maksimum wspolczynnika oporu).
A ~ 192 m^2 ~ 13 * (15 m^2),
15 m^2 jest tu faktycznym polem powierzchni dolnej skrzydła (tj. fragmentu skrzydła). Zespol pogwalcil fizyke o czynnik co najmniej 13 (co najmniej, bo jesli doda sie jeszcze skladowe przyspieszenia wzdluz osi Y polnoc-poludnie i uzyje lepszego przyblizenia, niz kolo Forda Perfecta, to zakladam, ze mozna dostac jeszcze wieksze przyspieszenie).
Skrzydło Biniendy na swym wirażu powietrznym w odległości 6 m od brzozy jest hamowane jak prostopadła plyta o powierzchni ~192 m^2, zamiast faktycznych 15 m^2. Jak widac, skrzydo Biniendy paradoksalnie konkuruje z calym nienaruszonym skrzydlem tupolewa, ktore ma 200 m^2, ale zachowujac oczywiscie mase zaledwie 600 kg!
Jaki efekt fizyczny moze zmodyfikowac ten błędny wynik? Okazuje się że żaden, jeśli chodzi o rząd wielkości! Cd~1.2 to maksymalny opór nieobracajacego się, ustawionego na sztorc skrzydła. ale obracajace sie skrzydlo ma podobny, a nawet mniejszy Cd niz obracajace. Mozna to latwo policzyc. Co prawda jedna strona skrzydla stawia wiekszy opor, ale druga mniejszy, co daje w sumie odrobine wiekszy Cd, ale usrednienie po obrocie (w ktorym skrzydlo chwilami praktycznienie daje sily oporu), w koncu daje mniejszy <Cd> ~ 0.8 po dlugim czasie, a na wirazu moze Cd~1. A zatem ani obrot, ani wartość V mniejsza niz założyłem, nic nie dają. Czy to nowa fizyka smolenska, czy tylko ktos niechcacy wstukał pole powierzchni A w ft^2 a mialo byc w m^2, albo coś było nie tak z jednostami gęstosci powietrza albo masy skrzydła? Innym możliwym wyjaśnieniem byłoby użycie metody CFD o niewłasciwej zdolnosci rozdzielczej. Znam takie programy, ktore błędnie użyte dadzą kompletenie niefizyczne wyniki, ponieważ bedą źle reprezentowały powietrze za przeciągnietym mocno skrzydlem, co zaniży mocno jego ciśnienie i da nierealną siłę oporu, jaką widzimy na trajektorii.











Komentarze
Pokaż komentarze (242)