30. Aerodynamika beczki smoleńskiej najprościej, jak można

[Wersja z poprawionymi obliczeniami, oryginalny tekst zawierał pomyłki i literówki. Styczeń 2018.]

"Things should be as simple as possible, but not simpler" (A. Einstein o edukacji)

W rozdziale 28-ym bloga skomentowałem obliczenia różnicy sily nośnej przed i po urwaniu końcowki lewego skrzydla PLF 101 ktore zostaly zaprezentowane w tej animacji, i porównałem wyniki mojego programu aerodynamicznego liczacego siły i momenty sił medotą panelową VLM z oszacowaniami robionymi przez inne osoby. Tutaj pokażę analityczną, uproszczoną, metodę obliczeń aerodynamicznych, która daje wyniki zbliżone do pełniejszej teorii pół-numerycznej zaprezentowanej wcześniej. Nawet trójwymiarowa trajektoria przewidywana przez obliczenia analityczne nie jest najgorsza! Ten rozdział to kropka nad "i" w modelowaniu beczki. Pokazuje, ze nawet uproszczone teorie sa zgodne z zasadniczymi sladami na ziemi i w rejestratorach.

Pisząc artykuł do żurnala mechaniki teor. i stosowanej JTAM zauważyłem, że istnieje proste heurystyczne wyprowadzenie zasadniczych dwóch wielkości dawanych przez wspomniane wyliczenia robione uogólniona metodą panelową Prandtla-Weissingera. Daje to bezpośredni wgląd w to, skąd biorą się konkretne wartości przyspieszenia i tempa obrotu, bez potrzeby obliczeń numerycznych, jeśli naturalnie nie żadamy wysokiej dokładności. (Te rzeczy leżą u podstawy dowodu, że tupolew obrócił się niemal na plecy w czasie 4.7s, że przelecial tuż nad terenem ponad 300m po dokładnie tej trajektorii, o której mówią nam teraz pozostałe pod Smoleńskiem, połamane gałęzie i drzewa, że spadł dokładnie tam gdzie spadł, no i że nie było do tego potrzeba żadnych cudów, maskirowek ani zamachów dwubombowych. Dlatego są tak ważne.)  

Opisze analityczne oszacowania nie dlatego, ze metody pół-numeryczne przeze mnie stosowane (trzeba numerycznie rozwiazac  uklad rownan liniowych) są  aż tak skomplikowane, że niemożliwe do powtórzenia. W istocie, każdy student wyższych lat fizyki lub inżynierii lotniczej potrafi takie obliczenia przeprowadzić pisząc samodzielnie program w Matlabie czy innym języku. Wiem to stąd, ze jeden z nich, David, korzysta z mojej pomocy w studiach nad takimi rzeczami na zaliczenie w ramach kursu PSCD01, który jest końcowym projektem indywidualnym w zakresie nauk fizycznych (David chce być doktorantem w naszym znanym w świecie instytucie aeronautyki na UofT). Opiszę je, bo tak sie robi w nauce: porównanie metod analitycznych i pół-numerycznych wykazuje, że te drugie nie zawieraja żadnego grubego błędu, że można zaufać wynikom. Bez wyliczeń analitycznych, w ekstremalnym przykładzie czysto numerycznych obliczeń przy użyciu programu LD-DYNA, wiedzieliśmy do czego może dojść. Wyniki mogą być wręcz niefizyczne. Ale jak mowię, to przypadek ekstremalnie jednotorowego podejscia do zagadnienia.

W przypadku moich obliczeń macierzowych, droga naszkicowana jest na tyle dokładnie, ze wiele osób może ją przebyć ponownie i potwierdzić wyniki. Jednak nie wszystkim będzie się chciało wnikać w szczegóły moich obliczeń, ani też nie każdy usiądzie by rozwiązać 400 równań z 400 niewiadomymi, żeby policzyć (jak to tu opisałem) :

(i) że tutka zaraz po przycięciu skrzydła do 13m rozpiętości rozkręca przechył w tempie dω/dt ~ 83^o/s²(bez uwzgl. lotki;  z uwzgl. lotki to niecałe 80^o/s²; już to samo pokazuje ze pozostała prawa lotka nie miała najmniejszej szansy na zahamowanie beczki),

(ii) że tutka przy takim obciążeniu (n=1.32g) jakie miała przy brzozie Bodina nie może obracać się szybciej, niż około ω ~ 48^o/s.

To są właśnie te zasadnicze dwie liczby, dla uzyskania ktorych liczyłem dokładnie aerodynamikę samolotu. Liczyłem całą siatke modeli, ale okazało się, że wszystkie je można opisać jednym czy dwoma wzorami analitycznymi z dokładnością paru procent; wzorami które zawierają dwie stałe podane powyżej (bądź bliskie im wartości, jeśli chcemy uwzględnić  szczegóły takie, jak odchylenie kierownicy wolantu w prawo).

Reszta moich obliczeń to osobna symulacja dynamiczna opisana w uprzednich rozdziałach, oparta częściowo na danych ze skrzynek (n(t), pochylenie(t), V(t)), a częściowo na rekonstrukcji dynamicznej przechyłu i odchyleń w pionie i poziomie od orginalnej trajektorii sprzed brzozy Bodina. Ale te obliczenia podałem juz w całości, także jako dobrze udokumentowaną treść programu w jezyku IDL, zresztą programu nieco prostszego niż ten liczący dwie opisane powyżej wielkości.

 

MOMENT BEZWŁADNOŚCI

Ponieważ do policzenia dω/dt potrzeba znajomości momentu bezwładności I_xx wokół osi podłużnej, pozwolę sobie naszkicować jak się wyznacza I_xx. Dzielimy myślowo samolot na jak najwięcej części składowych: kadłub, bagaże, pasażerowie, paliwo w osobnych kilku zbiornikach, skrzydła, stateczniki i tak dalej. Następnie ze znanej geometrii samolotu dość dokładnie możemy ocenić średnio-kwadratową odległość od osi tych części składowych. Jest to jakby promień równoważnego walca mającego taki sam moment bezwładności, jak dana część.

Czasem można użyć do wyznaczenia tego promienia prostego całkowania, np. trzeba to zrobić w przypadku rozciągłych obiektów - skrzydeł. Innym razem ta odległość jest od razu oczywista, jak np. w przypadku silników. W takim razie potrzeba już "tylko" wyznaczyć masy poszczególnych składowych. I to nie jest łatwe do wyszukania na sieci! Dokładne plany konstrukcyjne i dokładne masy to szczegóły techniczne znane producentowi, ale na ogol strzeżone przed okiem postronnych. Jednak te masy trzeba znać, by projektowac sensownie nowe samoloty i nie zaczynać zawsze od Adama i Ewy. Dlatego w pracach z bibliografii bloga takich jak: Sadraey (2009) i Kroo (2006), oraz Cleveland (1970), rozwijane sa prawa skalowania. Pomagają one zrozumieć w oparciu o wytrzymałość materiałów i zasady budowy skrzydła kesonowo - dźwigarowego, dlaczego masa skrzydeł skaluje się tak a nie inaczej wraz z całkowitą (maksymalną) masą startową samolotu transportowego, a po tym jak sie wyprowadzi odpowiednie zależności (Kroo 2006), jak się ta teoria ma do rzeczywistości - w oparciu o znane dawne konstrukcje samolotów. I te zgadzają się z prawami skalowania, jeśli chodzi o skrzydła. Dlatego mówię tu tyle o skrzydłach, ponieważ nawet jeśli pomylimy się trochę w ocenie masy kadłuba, nie będzie to bardzo ważne dla momentu bezwładności wokół osi podłużnej (kwadrat odległości jest stosunkowo mały), najważniejsze jest natomiast ocenić dobrze mase skrzydła, a także masę zespołu podwozia, bo ciężkie wózki koła głównego są oddalone aż o 6m od osi.

Wstawiłem do wzoru Kroo wartości odpowiadające TU-154M i otrzymałem oszacowanie z prawa skalowania równe 11.4 t dla masy strukturalnej skrzydła o kształcie skrzydła tupolewa, zaprojektowanego na wytrzymywanie przeciążeń do 2.5g*1.5 (gdzie 1.5 to lotniczy margines bezpieczeństwa). Po dodaniu masy obiektów siedzących w skrzydle ale nie nadających mu żadnej wytrzymałości, co stanowi typowo 25% dodatkowej masy, otrzymałem masę nieuszkodzonego skrzydła (tj. obu skrzydeł) równą 14.2 t. Masa strukturalna 11.4 t zgadza sie wspaniale z całym szeregiem mas w historycznych konstrukcjach takich jak: B 707, DC-8 DC-10, B 737, B 727 i in. Wszędzie tam, nota bene, jako reguły kciuka moża użyć zamiast skomplikowanego wzoru Kroo po prostu 11% TOW (max take-off weight) i będzie ok. Nota bene, dr Berczyński z zespołem twierdzi, ze skrzydło tupolewa było niesłychanie masywne, co jest wyssane z palca. Masa uzasadniona tutaj zgadza się z moimi wcześniej opublikowanymi w blogu ocenami pola przekrojów poprzecznych aluminum D16 w skrzydłach.

Masy i równoważne promienie sa w tupolewie następujące:

utracona końcowka skrzydła: 0.7t w odległości 16m,

kadłub wraz pasażerami i cargo: 40t w odl. 1.5m,

paliwo: 6t w odl. 2m oraz 5t w odl. 3.7m (dwa rodzaje zbiorników),

silniki: 6t w odl. 3.7m,

nieuszkodzone skrzydła: 14t w odl. 8m,

stabilizatory: 4t w odl. 5m,

podwozie wraz konsolami: 4t w odl. 6m.

________

Masa całkowita 78.6t przez zderzeniem z brzoza, 77.9 po nim.

Moment bezwładności I_xx = 1405 t*m² przed utratą, oraz

 I_xx =1223 t*m²

po utracie końcówki skrzydła. (ta wartość zawiera w sobie malutka poprawkę na te okoliczność, ze oś bezwładności przesuwa sie o 0.125m w prawo po utracie końcówki skrzydła). Wynik ten odpowiada masie tupolewa (po urwaniu części skrzydła równej M=78 ton=78 tys. kg) rozłożonej na walcu o promieniu prawie r_x=4 m, tak że

I_xx = M r_x². 

 

 

WYPROWADZENIE MOMENTU SIŁY NA POCZĄTKU BECZKI

Teraz możemy już przejść do zasadniczego oszacowania heurystycznego momentu siły T (ang.: torque) i  ściśle z nim związanego dω/dt, oraz maksymalnej pr. kątowej ω w czasie beczki.  To będzie proste oszacowanie, ale nie prostsze niż konieczne (Einstein mówił: trzeba wszystko wyjaśniać tak prosto jak sie da, ale tylko tak i nie prościej.) Przyjmiemy do oszacowań zasadniczy wynik teorii skrzydła o skończonej długości Ludwika Prandtla: siła jest tym "lepiej" rozłożona wzdłuż rozpiętości skrzydła, im bardziej jej wykres zbliżony jest do elipsy. W jakim sensie "lepiej"? W sensie minimalnego oporu indukowanego (zob. polskie wiki pt . Opór aerodynamiczny a lepiej te angielska stronę).

Skrzydła tupolewa z ich dużym skosem zaprojektowane zostały tak, że rozkład siły (wyliczony np. przez mój program aerodynamiczny) nieobracającego się skrzydła jest w istocie dość podobny do tej idealnej ze względu na opór indukowany funkcji

dF/dy =  f₀ (1 - y²/S²)^1/2

gdzie  f₀=const (oczywiście ta stała jest proporcjonalna do ciśnienia dynamicznego ρ V²/2, ale ta informacja nie będzie nam tu potrzebna, wyliczymy f₀ ze znanego przeciążenia). To podobieństwo nie jest oczywiste, bo kształt skrzydła tupolewa nie jest wcale zbliżony do eliptycznego. 

S = długość czy dokładniej pół-rozpiętość skrzydła. W naszym problemie rozpiętosci lewego i prawego skrzydła równają się

L = 13 m

R = 18.77 m

i takie wartości  stałej S należy przyjąć  na odpowiednich skrzydłach. Na obu skrzydłach przyjmijmy wiec rozkład eliptyczny siły o tej samej wartości siły maksymalnej, ale o rożnej rozpiętości. W naszym oszacowaniu dla uproszczenia zaniedbujemy wpływ wąskiego kadłuba, gdyż wyniki są znacznie bardziej czułe na to, co dzieje się na końcach skrzydeł, niż przy kadłubie.

Całkując iloczyn ramienia działania siły y oraz siły dF(y), dostajemy wkład dT do momentu siły T₀ (indeks 0 wskazuje, że mowa o zerowej szybkości obrotu skrzydła). Całkowanie zaczynamy na kikucie lewego skrzydła przy y=-L, a kończymy na końcu prawego przy y=+R.  Zatem

T₀ = ∫_-L^R (dF/dy) y dy.

Używając powyższego wzoru na dF/dy, osobno dla skrzydła lewego i prawego, dostajemy

T₀ = (f₀/2) (R²-L²)  ∫₀¹  (1 - x)^1/2 dx = (f₀/3) (R²-L²)

Potrzebną nam wartość f₀ wyznaczamy ze znanej siły nośnej F, równej F = n M, gdzie M to masa samolotu, zaś n jest przyspieszeniem pionowym środka masy (1.32 g ~13 m/s²):

F = ∫_-L^R (dF/dy) dy = f₀(R+L)  ∫₀¹  (1 - x²)^1/2 dx = (π f₀/4) (R+L) = n M,

f₀ = 4nM/[π(L+R)].

Wstawiając f₀ do wyrażenia na moment siły, mamy

 T₀ =  (4/3π)(R-L) n M

czyli moment siły to siła  F=n M razy ramię działania równe (4/3π) (R-L).

Pozostaje nam zapisać przyspieszenie kątowe krótką chwilę po urwaniu skrzydła jako

 dω/dt =  T₀/ I_xx = (4/3π) (R-L) n M/I_xx= (4/3π) (R-L) n/r_x²

Wstawiamy wartości opisujące tupolewa (n = 1.32 g = 12.95 m/s², r_x = 4 m, R = 18.77 m, L = 13 m)  i dostajemy oszacowanie

To oszacowanie jest o ok.jedną trzecią większe niż dokładniejsza wartość dω/dt ~ 83^o/s², wyliczona dla skrzydła z opuszczonymi jak w tupolewie klapami i niewychyloną lotką, metodą macierzową, z uogólnionej teorii Prandtla-Weissingera.

 

KOŃCOWA (MAKSYMALNA) PRĘDKOŚĆ KĄTOWA PRZECHYŁU

Teraz chcemy uwzględnić wpływ obrotu wokół osi podłużnej. Ponieważ siła nośna zależy od lokalnego kąta natarcia strugi powietrza na linie średniego profilu skrzydła, zapiszmy ten kąt (ang.: AOA) jako α:

 α = α_kadl - α_wzn + α_skr - α_L0 - α_obr

(kadl = kąt kadłuba czyli pochylenie do poziomu; wzn = kąt wznoszenia ; skr = kat skręcenia (washout) skrzydła; L0 = kąt zerowej siły nośnej, na przykład w tupolewie z klapami opuszczonymi 36^o wynosi on średnio dla całego skrzydła tuz nad ziemia, α_L0= -6.6^o ;  obr = kąt wywołany obrotem skrzydła robiącego beczkę). Zauważmy, ze α to taki kąt natarcia, który znika gdy siła nośna znika; nie jest to kąt natarcia w stosunku do jakichś innych, bardziej typowych kierunków, jak np. oś samolotu. Nie jest to więc kat AOA (angle of attack) taki, jakim się go zazwyczaj widuje w podręcznikach i instrukcjach obsługi samolotu TU-154. Przy AOA=0 samolot produkuje bowiem dodatnią siłę nośną, a my musimy ustalić kąt do którego siła nośna będzie, w przybliżeniu małych kątów, wprost proporcjonalna.

Kąt α_obr to lokalna prędkość pionowa danego fragmentu skrzydła podzielona przez prędkość postępową V = 75 m/s), co daje ten mały kąt w radianach. Pomijając obrót i przyjmując średni kat skręcenia skrzydła równy 1^o, co jest średnia arytmetyczna z ekstremalnych kątów skręcenia +3 i -1 stopni na początku i końcu prawego skrzydła, przy brzozie tupolew miał

 α₀ =  α_kadl - α_wzn + α_skr - α_L0 

 α₀ ~ 13.5^o - 4.8^o   +1^o   +6.6^o  ~   16.3^o

Uwzględniając obrót wokół osi podłużnej z prędkością kątową ω,  mamy

 α = α₀ - ω y/V  = α₀ (1 - ω y/Vα₀).

Zatem T = ∫_-L^R f₀ (1 - y²/S²)^1/2  y (1 - ω y/Vα₀) dy

gdzie S=L  dla  y<0,  zaś  S=R  dla  y>0.

W wyrażeniu podcałkowym (1-ωy/Vα₀), 1 produkuje w wyniku końcowym T₀, natomiast (-ωy/Vα₀) produkuje moment siły zależny od rotacji, nazwijmy go  T_rot

  T_rot = -f₀ ω /(Vα₀)  ∫_-L^R  (1 - y²/S²)^1/2 y² dy.

Można w całce zamienić zmienne z  y na t, gdzie t=(y/S)², a wtedy całka przybiera postać typu (1/2) ∫₀¹  [t(1 - t)]^1/2 dt =  π/16.  Asymptotyczna prędkość kątowa obrotu to takie ω_max, dla którego  T = 0.

T =  T₀ [1  - (3π/16) (R³+L³)/(R²-L²) (ω_max/ Vα₀)] = 0, wiec

ω_max = (16/3π) (R²-L²)/(R³+L³) Vα₀

Wstawiając teraz L=13 m i R=18.77 m, V=75 m/s, oraz  α₀ ~16.3^o, dostajemy następujące oszacowanie asymptotycznego tempa obrotu:

co jest dość dokładnym oszacowaniem tej wielkości, równym 90% dokładniejszej wartości  ω ~ 48^o/s, otrzymanej z uwzględnieniem klap, lotki, steru kierunku, stopniowego skręcenia kształtu skrzydła, skosu i zmiennej szerokości skrzydeł oraz wzajemnego oddziaływania różnych części skrzydeł na lokalne kąty ataku strug w wyniku produkcji wirów, a także wpływ kadłuba  (uogólniona teoria Prandtla-Weissingera).

 

WYNIKI ALTERNATYWNEJ SYMULACJI 

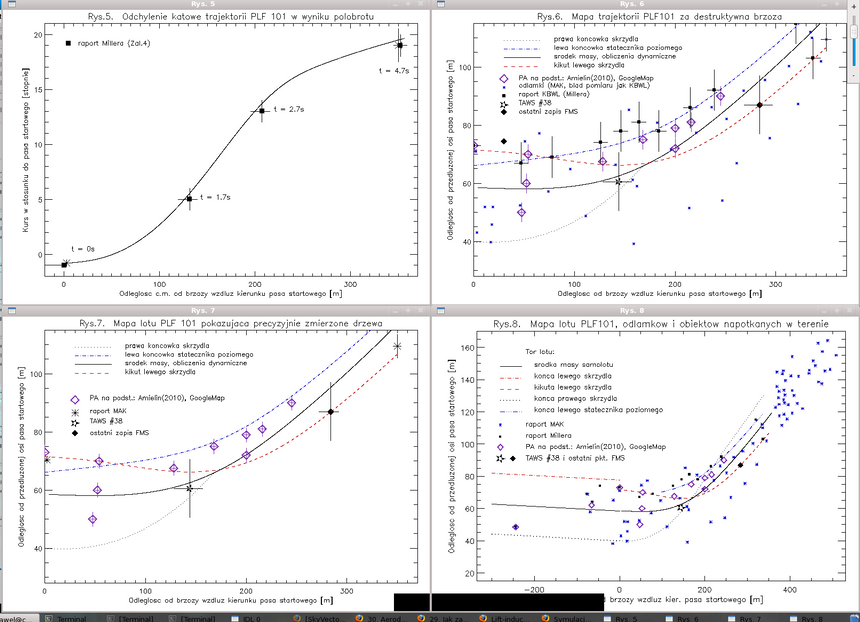
Jeśli użyjemy wyprowadzonych w przybliżeniu wartości 43^o/s zamiast 48^o/s oraz 114^o/s² zamiast 80^o/s², dostaniemy następującą trajektorię: rys. 1-4, a tutaj rys. 4-8, która nie pasuje do danych smoleńskich aż tak dokładnie, jak wyliczona poprzednio, ale można zauważyć, że także pasuje "nieźle". Jest tak zapewne dlatego, że o ile przyspieszenie obrotu wzrosło w mniej dokładnym obliczeniu, to jednak końcowy kąt obrotu przy uderzeniu w ziemię nie zwiększył się tylko zmalał do 140 stopni przechyłu, gdyż asymptotyczne szybkości obrotu w mniej dokładnym oszacowaniu są zauważalnie mniejsze, niż w teorii pełniejszej. Błędy się częściowo skasowały, a trajektoria --nawet ta niedokładna-- ma sens: kikut lewego skrzydła nadal leci nad a nie pod ziemią (4-9m zamiast poprzednich 5-10m nad terenem), samolot schodzi ok. 20 stopni z kursu i tak dalej. Niewielkie zmiany omawianych wyników aerodynamicznych nie są więc ważne dla scenariusza katastrofy, który został tu po raz kolejny potwierdzony. 

 

SUMMA SUMMARUM  

Uzyskaliśmy proste oszacowania dwóch najważniejszych wielkości cechujących samolot TU-154M po utracie 1/3 lewego skrzydła: przyspieszenia kątowego i maksymalnej prędkości kątowej przy znanym przeciążeniu. Te oszacowania sa zgodne z dużo uważniej uprzednio wyliczonymi wartościami,  z dokładnością, odpowiednio, ok. 37% i 10%. Podobne wyliczenia wielu z was, np. andrzejmat, zrobiło już dawno. Mi było po prostu łatwiej pokazać na 3-wymiarowej trajektorii co z tych wartości wynika. 

 

Na koniec dwa postscriptum:

1.  O ile przyspieszenie kątowe tupolewa miało rzeczywiście początkowo przybliżoną wartość 80 stopni na sekundę kwadrat, to maksymalna prędkosc kątowa 48^o/s nie została jednak przez samolot osiągnięta, ponieważ po czasie potrzebnym do zbliżenia się do niej (~2 s) zmieniły się warunki lotu: wzrosło a zaraz potem spadło przyspieszenie n(t) i zmieniły się wychylenia sterów. To wszystko uwzględniono w symulacji dynamicznej Artymowicza (2014, JTAM, in prep.) posługującej się wyliczonymi tam parametrami i prawami skalowania.

2. Nie wspominałem jeszcze o dwuczęściowym wywiadzie  prasowym dla polonijnego dziennika kanadyjskiego: dziennik Dziennik. Zachęcam do kliknięcia na marginesie po prawej stronie w dziale 'Polecane strony'.

Dodatkowo, dla części agnostycznej i antyreligijnej Polaków, ktorzy czytają czasopismo Fakty i Mity, tez udzielilem tam wywiadu ktory ukazał się wczoraj i został zalinkowany na "Polecanych stronach".

Informacji udzielam (bez wynagrodzenia!) wszystkim, od FiM do GP i ND. Powiedziałem to dziennikarzom tych ostatnich gazet, którzy jako jedyni (prasy tzw. lemingowej nie było) znaleźli sie w Kazimierzu nad Wisłą w końcu maja br. Jeszcze do tej pory nie skontaktowali się ze mną. Ja to rozumiem i czekam cierpliwie, nie obiecywali mi nic przecież. Mają już moje zdjęcia stamtąd, robiliśmy w pięknej kamienicy, gdzie odbywała się konferencja.