61. Teoria fugoidy i oscylacje na zniżaniu końcowym tupolewa 101

Mam nadzieję, że tegoroczna rocznica katastrofy samolotu PLF 101 w Smoleńsku będzie pierwszą okazją do spokojnej zadumy, w odróżnieniu od brudnych, politycznych spektakli organizowanych dawniej. 

W tym duchu przedstawię dziś zjawisko oscylacji podłużnych płatowca zwane fugoidą. Tym uzupełnię omawiany ostatnio w rozdz. 59-60 temat nieustabilizowanego podejścia tupolewa, kontynuowanego aż pod poziom lotniska zanim samolot minął BRL (bliższą radiolatarnię z markerem środkowym, MM) na podejściu do pasa 26. Zobaczymy tu między innymi dlaczego ten rodzaj oscylacji powstaje, dlaczego i jak szybko zanika, i dlaczego ma tak uniwersalne własności (okres fugoidy nie zależy niemal od rodzaju i konfiguracji samolotu, ciągu silników, pogody i wysokości lotu; zależy tylko od prędkości wskazywanej względem powietrza, IAS). Będzie okazja zastanowić się czy tego typu oscylacja faktycznie wystąpiła i czy mogła stworzyć dodatkowe zagrożenie na zniżaniu końcowym tupolewa. 

 

1. ZABURZENIA RÓWNOWAGI 

Sześć minut przed końcem lotu wysunięto mechanizację skrzydła (klapy za skrzydłem i slaty na krawędzi natarcia) oraz podwozie. Na dwie minuty przed końcem lotu zaszły dalsze zmiany kąta ustawienia statecznika, i zwiększenie kąta klap z 28 do 36 stopni. Przy takiej rekonfiguracji lub nawet chwilowym pociągnięciu steru na siebie, tupolew PLF 101 pod Smoleńskiem miał normalną tendencję do robienia tzw. balona. To slangowe określenie na krótkotrwałe wznoszenie przechodzące w opadanie, związane ze zmianą kąta natarcia. Rekonfiguracja powodować może wzbudzenie modów oscylacji m.in. przechyłu kadłuba.

Niektóre oscylacje są krótkookresowe i bardzo szybko tłumione. Natomiast fugoida, czyli długookresowe oscylacje podłużne, trwają znacznie dłużej, do kilku minut. Dopóki automat ciągu (AT) rzeczywiście potrafi utrzymać stałą prędkość, klasyczna fugoida b. szybko zanika. Ale dnia 10.04.10 AT zmniejszył ciąg do minimalnego lotnego, tj do "biegu luzem", czyniąc TU-154M  prawie szybowcem. Prędkość nie spadła od razu do zaprogramowanej - piloci zażądali bowiem jednocześnie bardzo stromego opadania. Sądzę, że zniżanie końcowe (ostatnie dwie minuty lotu z wysokości 500 m do wysokości 0 m nad pasem odbywało się na tle fugoidy smoleńskiej, która dała zafalowanie trajektorii i duże oscylacje prędkości omawiane niedawno w rozdz. 60. bloga.

Wg mnie piloci kręcili wielokrotnie gałką SPUSK-PODJOM (w dół--w górę) trymera steru wysokości. Kręcili, co ważne, w obu kierunkach, nie dla zabawy, tylko reagując na tendencje podnoszenia i opuszczania się dziobu samolotu w fugoidzie. Wcale przy tym jej nie likwidując, ale też i nie destabilizując oscylacji (nie wzbudzając groźnych PIO = Pilot-Induced Oscillations). Każdy powinien wyrobić sobie o tym własne zdanie, więc proszę uważać i jak zawsze, nie brać niczego na wiarę.

Fugoida nie jest powszechnie znanym zjawiskiem, ponieważ samoloty pasażerskie mając automatykę wykorzystywaną poprawnie i na właściwym etapie lotu, likwidują zarówno krótko- jak i długookresowe oscylacje podłużne. Polskie wydanie wikipedii nie tłumaczy jej, angielskie zaś słabo. Uzupełniam te braki poniższym tekstem o klasycznej, fizycznej analizie zjawiska fugoidy, który używałem jako rozszerzenie wykładu dla studentów nauk fiz. o układach dynamicznych "Nonlinear Physics and Chaos" oraz jako część wykładu mechaniki dla fizyków (Mechanics: from Oscillations to Chaos) na uniwersytecie w Toronto.

2. TEORIA OSCYLACJI PODŁUŻNYCH

2.1. Omówienie równań ruchu  

Płatowiec w locie szybującym, albo ptak w locie nie machający skrzydłami, to nieliniowy, wielowymiarowy układ dynamiczny. Kiedy jednak utrzymuje lot nieprzechylony na bok, wymiar problemu spada do dwóch.  Trzeba ułożyć równania na zmiany prędkości i pochylenia trajektorii samolotu. W tych równaniach znajdą się efekty siły oporu aerodynamicznego oraz siły nośnej płata. Te prostopadłe do siebie siły są proporcjonalne do kwadratu prędkości postępowej samolotu względem powietrza, którą oznaczymy literą v. Zdefiniujmy stałe L i D jako współczynniki proporcjonalności:

przyspieszenie siły nośnej = L v²;          przyspieszenie siły oporu = D v².

Zwracam uwagę, że L i D będą w tym rozdziale wymiarowymi współczynnikami przyspieszenia od odpowiednich sił, a nie siłami F_L (siła nośna) i F_D (siła oporu), ani bezwymiarowymi współczynnikami C_L i C_D. L i D to po prostu odpowiednie siły podzielone przez kwadrat (kalibrowanej) prędkości wskazywanej, albo C_L i C_D  przemnożone przez powierzchnię skrzydła i połowę standardowej gęstości atmosferycznej,  i podzielone przez masę samolotu. Ale nie komplikujmy tu niepotrzebnie wyprowadzenia powtarzając te wyrażenia w kółko - używajmy naszych prostszych stałych L i D. Stosunek L/D = C_L/C_D.

Zakładamy poniżej, że L i D nie zależą od prędkości. L zmienia się liniowo z kątem natarcia (AOA). Rownież D jest zależne od AOA, gdyż siła oporu to suma oporu formy (parasitic drag)  i oporu indukowanego, zależnego od kwadratu C_L, a więc także od formy liniowej AOA do kwadratu. Kąt natarcia był mało zmienny w czasie oscylacji, utrzymywał się w pobliżu wartości 5^o ~ const (analizowaliśmy to w rozdziale 59), to pozwala nam w pierwszym przybliżeniu uznać L, D, i L/D za stałe. Ujemna siła oporu była liczbowo redukowana przez mniejszą, dodatnią, siłę napędu. Pomijamy tę ostatnią, pozostawiając wyprowadzenia z udziałem stałej siły ciągu jako dodatkowe ćwiczenie dla czytelnika. Poprawki na okres oscylacji i czasu jej tłumienia są bardzo niewielkie. Wynika to z tego, że siły oporu i ciągu są małe w stosunku do siły nośnej. Dlatego uprościmy analizę do przypadku zerowego ciągu (przypadku szybowca). Naturalnie, pisząc np. symulator lotu nie moglibyśmy zaniedbać ciągu silników, gdyż dostalibyśmy złe nachylenie trajektorii, ale jej zafalowanie, które tu badamy, byłoby b. podobne.

Małemu przyrostowi czasu dt towarzyszy zwiększenie wektora prędkości o wektor dv. Ten wektor ma składową radialną związaną ze wzrostem długości (zapiszemy ją jako skalar dv) i składową poprzeczną, wywołaną obrotem wektora prędkości v o mały kąt dθ, gdzie θ jest kątem trajektorii do horyzontu, ujemnym przy trajektorii opadającej ku ziemi.  Sformułujmy dwa równania: pierwsze o przyspieszeniu wzdłuż trajektorii, a drugie o przyspieszeniu prostopadłym do niej: 

dv/dt    = -g sinθ  - D v² 

v dθ/dt = -g cosθ + L v² 

gdzie g = 9.81 m/s² . Pierwsze wyrazy po prawych stronach to składowe pionowego wektora przyspieszenia siły ciężkości.

2.2. Rozwiązania stacjonarne

Rozwiązania stacjonarne odpowiadają gładkiemu zniżaniu bez oscylacji. Punkt stały układu dynamicznego oznaczony jako v = v* oraz  θ = θ*, uzyskujemy przez przyrównanie pochodnych v i θ do zera. To taki zbiór wartości zmiennych układu, że stają się one niezmienne (miłośnicy matematyki wspomną tu słynne tw. Banacha o punkcie stałym). Otrzymujemy

(v*)² = g / (D² + L²)^1/2 

tan θ*  = -D/L

Samoloty, a zwłaszcza szybowce, są zaprojektowane tak, by mieć mały minimalny stosunek oporu do siły nośnej: D/L << 1, faktycznie osiąga się D/L = 1/10 ... 1/60.  Siła oporu jest 10 do 60 razy mniejsza niż siła nośna przy optymalnych prędkościach/kątach natarcia. Ten czynnik nazywa się doskonałością aerodynamiczną płatowca (glide ratio, L/D ratio). Dzięki temu możemy zastąpić pierwiastek kwadratowy (D²+L²)^1/2  przez L, z małym błędem względnym ~(D/L)² < 0,01.  Z podobną dokładnością  tan θ* = θ* +O( θ*³) ~  θ*. 

v*² = g/L      lub   inaczej:     L v* = g/v*, 

albo po prostu  M L v*² = siła nośna = ciężar samolotu = M g.

θ* = -D/L.          (Ogólniej można pokazać, że:    tan θ* = -D/L + F_ciągu /F_L .)

W przypadku starszych szybowców θ* = -D/L ~ -1/30 radianów (-2^o; ok. -1^o dla najlepszych i najnowszych). Samolot pasażerski TU-154M w konfiguracji przelotowej będzie leciał bez napędu 17 razy dalej niż opadał, pod kątem 3.4 stopnia. Doskonale szybujący ptak albatros osiąga L/D ≈ 22, więc θ* ~ -1/22 rad lub -2.6^o. Ptaki te potrafią okrążyć cały świat, lecąc 1000 km dziennie. Dla osiągnięcia wysokich współczynników L/D, skrzydła muszą być bardzo wydłużone. W związku z tym zarówno szybowce, jak i albatrosy mają takie właśnie skrzydła; rozpiętość skrzydeł tych ostatnich osiąga 3.4 m. Aby utrzymać skrzydła w pełni rozwinięte, albatrosy mają specjalny zamek na ścięgnach i nie używają do tego żadnych mięśni; stosują wznoszące się prądy powietrzne i wiatry, i nie marnują energii na trzepotanie skrzydłami, w odróżnieniu od wróbli, które mają strasznie niedoskonały współczynnik doskonałości L/D = 4, i opadają 1 m na każde 4 metry lotu szybującego. OK, wróćmy od ptaków, szybujących żab i latających ryb do lotu ślizgowego samolotu i jego oscylacji.

2.3. Paradoksalne sterowanie

Wyjaśnię pewną ważną rzecz. Dlaczego piloci (w tym autopiloci) tak dziwnie sterują samolotem na zniżaniu końcowym: aby zmniejszyć prędkość lotu, wcale nie zmniejszają ciągu silnika, a aby zwiększyć kąt opadania, wcale nie muszą zwiększać pochylenia kadłuba. Na odwrót:

(i) piloci zasadniczo kontrolują kąt opadania samolotu używając ciągu silnika, zaś

(ii) szybkość zmieniają pochylając samolot sterami lub trymerem.

Nie można pilotować jakoś prościej? Nie, to niewykonalne lub niebezpieczne. 

Otóż na zniżaniu końcowym zależy nam na najmniejszej, ale bezpiecznej prędkości v*, ok. 1.3 prędkości przeciągnięcia. Prędkość  gładkiego opadania v* = (g/L)^1/2 zależy tylko od L, tj. od kąta natarcia, który możemy zmienić sterami lub trymerem, gdyż L = C_L(AOA)  (ρ_std A/2M), zależy liniowo od AOA (por. rozdz. 59). Regulować v* można więc zasadniczo tylko zmianami AOA. Zmianami siły ciągu tego nie osiągniemy. Stąd reguła (ii). 

W ustabilizowanym podejściu, gdzie v* jest bliskie cytowanej wyżej bezpiecznej wartości,  AOA, C_L i v* są dla danego samolotu ustalone i nie powinny się zmieniać. To zaś ustala pewną wartość stosunku D/L, zależącego od AOA. Dlatego pożądane zmiany kąta θ* pilot osiąga bezpiecznie tylko zmianą F_ciągu, co stanowi regułę (i) podejść.

Inaczej, nie zmieniając mocy silników a zmieniając tylko trymowanie i wychylenie steru wysokości --> zmieniając AOA, pilot zmieni także v*. Jeśli zmniejszy kąt wznoszenia i V_z do bardziej ujemnych wartości, wtedy v* wzrośnie (to stało się przez błąd pilotażu na zniżaniu końcowym w Smoleńsku, AT nie umiał zmniejszyć v* do zaprogramowanych 280 km/h, prędkość długi czas pozostawała większa niż 300 km/h) - niebezpieczeństwem wtedy jest niedolecenie do pasa i CFIT,  do którego doszło. Jeśli mając w miarę poprawną v* pilot zwiększy kąt wznoszenia i Vz do mniej ujemnych wartości, wtedy v* spadnie - co wywoła niebezpieczeństwo przeciągnięcia. Dlatego właśnie chcąc zwiększyć lub zmniejszyć kąt podejścia, nie bawimy się trymerem ani sterem wysokości, tylko regulujemy moc silników, w dozwolonym zakresie. To jedyna bezpieczna metoda trafienia w strefę lądowania na pasie. 

Na podejściu końcowym PLF 101 do Smoleńska, po tym jak ciąg silników został zredukowany do minimum, bez dodania gazu tupolew nie mógł wyjść na trajektorię o bliższym zeru kącie opadania, trafiającą w pas startowy 26. Mógł to zrobić pilot zwiększając ciąg ręcznie, albo pozostawiając sterowanie ciągiem AT i zwiększając pochylenie samolotu odpowiednio wcześnie trymerem steru wysokości (kółko SPUSK-PODJOM). Falista trajektoria brała się prawdopodobnie z opisanych niżej oscylacji i próby ich kontrowania wspominanym trymerem, ustawionym jednak średnio na dużo za strome opadanie.

2.4. Stabilność rozwiązań stacjonarnych w ujęciu macierzowym 

Równania ruchu są nieliniowe, co jest typowe dla aerodynamiki, ale mogą i powinny być zlinearyzowane. Zrobimy to by pokazać, jaką stabilność ma szybowiec na małe odchylenie od równowagi. Mamy nadzieję, że ustalimy, iż punkt stały jest przyciągający, czyli mocno stabilny. W przeciwnym razie lot byłby możliwy, ale bardzo męczący dla pilota, ponieważ statek powietrzny stale (wykładniczo szybko) odbiegałby od początkowego toru lotu. W rzeczywistości samolot braci Wright był takim samolotem, trudnym do kierowania, ponieważ był nieco niestabilny. Zapiszmy zmienne układu jako

v = (1 + ε) v* ,   oraz       θ = θ* + φ, 

gdzie ε i φ są małymi, bezwymiarowymi odchyleniami prędkości i kąta (w radianach), których potęgi większe niż pierwsza można zaniedbać w rozwinięciach w szereg Taylora. Po linearyzacji, używając związku g/v* = Lv*, otrzymujemy

dε/dt =     -2 D v* ε     - (g/v*) φ 

dφ/dt =   2 (g/v*) ε        -D v* φ 

W postaci macierzowej, wygląda to tak:           dx/dt = A x,

gdzie  x = (ε, φ)^T  (wektor transponowany, składowe zapisane w pionie), zaś A jest macierzą 2x2 złożoną z czterech liczb (ich wskaźniki pokazują kolejno numer wiersza i kolumny macierzy):

a11 = -2D v* ,     a12 = -g/v* = L v* ,     a21 = 2g/v* = 2L v* ,     a22 = -D v* 

Macierz A ma zawsze dodatni wyznacznik det(A) := a₁₁a₂₂ - a₁₂a₂₁, 

det(A) = 2 (Lv*)2 + 2 (Dv*)2 > 0 ,

oraz ślad   tr(A) := a₁₁+a₂₂, czyli sumę wyrazów na diagonali, która jest tu zawsze ujemna

tr(A) = -3D v* < 0.

W teorii układów dynamicznych stabilność liniowa układu określa zachowanie się rozwiązań układu równań różniczkowych w bezpośredniej bliskości punktu równowagi, do czego wystarcza wiedza o współczynnikach macierzy A. Do pozytywnej stabilności typu oscylacji o malejącej amplitudzie wymagane są dwie rzeczy: po pierwsze tr(A)<0 (to już pokazaliśmy), a po drugie: kwadrat połowy śladu macierzy mniejszy niż wyznacznik macierzy:

tr(A)2/4 < det(A).

Udowodnię, że te warunki są dostateczne, poniżej. Zobaczmy najpierw czy drugi z nich jest spełniony. Podstawiając wyrażenia na tr(A) i det(A) do powyższej nierówności widzimy, że tak jest, gdy D/L < 8^1/2 = 2.82. Wtedy zachodzi

tr(A)2/4 - det(A) = (v*)2 [ D2/4 - 2 L2 ] < 0.

To formalny dowód, że na portrecie przestrzeni fazowej oscylacje są spiralą zbieżną. Wychylenia zmiennych v i θ są tłumione i to naturalnie, bez potrzeby stabilizacji przez wychylanie powierzchni sterujących.

2.5. Historia fugoid  Mikołaja E. Żukowskiego i Fryderyka W. Lanchestera

Znaleźliśmy, jak zobaczymy obliczeniowo poniżej, bardo powolne oscylacje samolotu w locie, które można obejrzeć w powietrzu tutaj:  https://www.youtube.com/watch?v=xvOnfxxaUmw  .

Polegają tylko na zmianach pochylenia samolotu, bez przechyłu. Obie te cechy odróżniają ten mod zaburzeń od znacznie szybszej oscylacji ślizgu i przechyłu, zwanej holenderowaniem (Dutch roll). Są znane w aerodynamice jako oscylacja fugoidalna. Termin ten został wymyślony przez brytyjskiego inżyniera i aerodynamika Fredericka W. Lanchestera, który jako pierwszy zbadał ten wariant zaburzeń, przyjmując D = 0. Słowa φυγή (fige) i εἶδος (idos) miały oznaczać razem "podobny do lotu". Niestety, Lanchester pomylił jednak dwa znaczenia angielskiego słowa lot (flight)! Po ang. flight oznacza albo ucieczkę albo lot. Wziął ze słownika angielsko-greckiego pierwsze słowo jakie napotkał, φυγή (fige), co znaczy "uciekać", a nie "latać" (petaxoun). Nazwa oscylacji dosłownie oznacza więc "jakby uciekająca", wbrew wykazanej naturalnej własności zanikania; ale co zrobić, skoro taka się przyjęła to jest :-) Już w 19. wieku inżynierowie zwolnieni byli z lekcji języków klasycznych.

Bez oporu aerodynamicznego i napędu (D = 0, co jest założeniem o sile ciągu zawsze dokładnie równoważącej opór) szybowiec nie opada (θ* = 0) i będzie oscylował w nieskończoność (ślad macierzy tr A będzie miał wartość zerową, co w analizie liniowej układów dynamicznych odpowiada cyrkulacji zamkniętej, periodycznej). Wczesny dokument aerodynamiczny Lanchestera "Szybowanie ptaków a możliwość lotu mechanicznego" został napisany w 1897 roku, dużo wcześniej, nim powstał pierwszy samolot. Wyraźnie wyprzedzał swój czas. (W 1927 roku zaprojektował być może pierwszy hybrydowy samochód "benzynowo-elektryczny"). W drugiej części dwutomowej książki o teorii lotu opublikowanej w 1907 i 1908 roku, do wglądu na mikrofilmie w bibliotece uniwersytetu torontońskiego, Lanchester opisał swą niegasnącą fugoidę bez oporu netto.

Po napisaniu tej notki natrafiłem na stwierdzenia w starych pracach ros., że twórcą pierwszych badań teoretycznych fugoidy (a także figury akrobacyjnej pętli, zob. ten rozdz. bloga pt. 'Aerodynamika - nie próbować niemożliwego' , ojciec aerodynamiki rosyjskiej Nikołaj Żukowskij, w wykładzie:  Жуковский Н.Е. О парении птиц. М., 1891. Z początku wątpiłem w to trochę, tym bardziej że nie mogłem dotrzeć do tego wykładu, ale szczęście uśmiechnęło się do mnie, gdyż został on opublikowany w r. 1922 przez niemiecką oficynę wydawniczą ( http://books.e-heritage.ru/book/10070071). Okazało się, że Żukowski faktycznie pierwszy napisał równania równoważne naszym dwóm równaniom różniczkowym na przyspieszenia wzdłuż i w poprzek trajektorii.
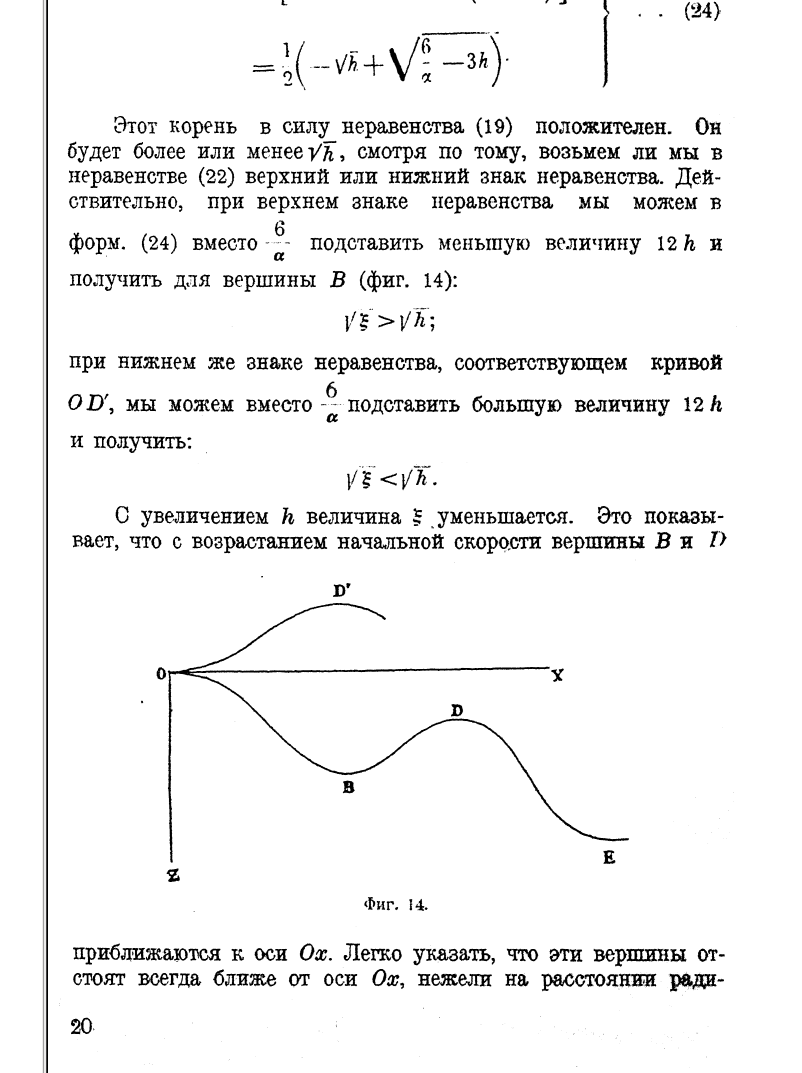
Co więcej, rozwiązał je metodą przybliżoną i podał wykresy trajektorii szybowania ze stałym kątem natarcia w obecności oporu powietrza, czego Lanchester nie zrobił. W ten sposób wykreślił rozwiązania opisujące: (i) pętlę, (ii) fugoidę. Na dowód pokażę tu dwie strony z jego ciekawej i bardzo wczesnej pracy o ruchu wszystkiego, co lata. Jedyne co mógł zrobić jeszcze przy użyciu swego aparatu matematycznego, ale nie zrobił, to obliczenie okresu długookresowych oscylacji fugoidalnych!

2.6. Zagadnienie własne i rozwiązania niestacjonarne 

W macierzowym problemie własnym poszukuje się rozwiązań, które są wprost proporcjonalne do wektora szybkości zmian,

dx/dt = λ x,      to znaczy:  dε/dt = λ ε;     dφ/dt = λ φ. 

Wartość własną (Eigenwert, eigenvalue) λ trzeba wyznaczyć, tak jak i rozwiązania na składowe wektora x. Rozwiązań problemu własnego poszukujemy w formie wykładniczej w czasie:  x = (ε, φ) ~ exp (λt), lub w postaci kombinacji liniowej takich członów dla dwóch wartości λ. Amplitudy zaburzeń zagadnienie własne nie wyznacza, zależy ona od wielkości początkowego zaburzenia równowagi. Podstawiając rozwiązania w poszukiwanej formie do  równania ruchu (dx/dt = A x), otrzymujemy równanie A x = λ x, które jest równaniem jednorodnym (A-λI)x = 0, co implikuje  det(A-λI) = 0, gdzie I jest macierzą jednostkową 2x2. Wyznacznik ten daje charakterystyczne równanie dla wartości własnych λ dowolnej macierzy A: 

(a₁₁- λ) (a₂₂ - λ) - a₁₂ a₂₁ = 0, 

λ² - tr(A) λ + det(A) = 0,

a stąd dwie wartości własne, które są sprzężonymi liczbami zespolonymi

λ =  tr(A)/2  ± i [ det(A) -  tr(A)²/4 ]^1/2 . 

Jeśli tr(A) jest ujemny (jak w naszym przypadku), to część rzeczywista λ  w wyrażeniu  exp(λt) opisującym przebieg czasowy zmian parametrów lotu powoduje tłumienie amplitudy zmian parametrów, czyli daje stabilność. Powołaliśmy się na ten fakt wcześniej, bez dowodu. Widać też, że aby zmiany czasowe miały charakter oscylacji, potrzebna jest dodatnia wartość wyrażenia w nawiasie kwadratowym; inaczej nie dostaniemy części urojonej λ i zgodnie ze wzorem Eulera, funkcji sinus i cosinus jako czynnik czasowy. To dowodzi, że do oscylacji potrzeba, by  tr(A)²/4 < det(A). W naszym przypadku otrzymujemy  

λ = - (3D/2) v* ± i [2 (g/v*)² - (3D v*/2)² ]^1/2 . 

W nawiasie kwadratowym można zaniedbać człon zawierający D, ponieważ przyspieszenie oporu aerodynamicznego, Dv*² , jest dużo mniejsze od g = Lv*² ,  co wynika z  D/L << 1. Zatem  

λ = -1/τ ± i ω, 

gdzie         ω = 2^1/2g/v* 

jest częstotliwością oscylacji, zaś

1/τ = (3/2) (Dv*) = (3/2^3/2 ) (D/L) ω 

jest szybkością tłumienia amplitudy; obie stałe mają jednostkę fizyczną 1/s = Hz. Stała czasowa τ to czas zmniejszania amplitudy oscylacji o czynnik e, natomiast okres oscylacji fugoidalnej równy jest

P = 2π/ω = 2^1/2 (π/g) v*.

Porównując τ  i  P, 

τ = 2/(3Dv*) = (L/D) (2^1/2/ 3π) P 

widzimy, że tłumienie fugoidy w dobrych szybowcach (L/D > 30) zajmuje τ > 14P/π ~ 4.5 okresów oscylacji. Źle zaprojektowane płatowce tłumią fugoidy lepiej(!), a nie gorzej: tłumienie trwa krócej. Słabe tłumienie oscylacji podłużnych przez większą część lotu to cena, którą chętnie płacimy za mały współczynnik oporu i wysoką doskonałość aerodynamiczną statku powietrznego.

Co uderzające, w pierwszym przybliżeniu, w którym robimy nasze obliczenia, okres fugoidy P nie zależy od niczego oprócz prędkości lotu IAS lub CAS: ani od tego, jak aerodynamiczny jest kształt samolotu i jak efektywnie wytwarza siłę nośną, jaki ma wsp. doskonałości L/D, pod jakim leci kątem pochylenia i natarcia, jak ciężki jest samolot i jak jest wyważony, jakie ma momenty bezwładności, ani jak gorące, gęste, wilgotne czy lepkie powietrze jest w danym dniu, na jakiej wysokości lecimy, czy wieje tam wiatr itd. Płatowiec nie musi nawet być szybowcem, może mieć napęd. Prostota wyniku powoduje, że to jedna z piękniejszych (choć przybliżonych) zasad aerodynamiki lotu.

Czy potrafisz powtórzyć Czytelniku wyprowadzenie ze stałym przyspieszeniem ciągu dodanym wzdłuż toru lotu, by udowodnić wyrażenie na θ* podane powyżej i uogólnić wyrażenia na ω oraz τ?

3. ZASTOSOWANIA, PORÓWNANIA, oraz ZNACZENIE FUGOIDY

3.1. Przykłady 

Nasza klasyczna (tj. równa lanchesterowskiej) formuła na okres fugoidy przewiduje 

P ≈ 45.3 s   [v / (100 m/s)] 

Ten wynik jest dokładnie taki sam, jaki dało pierwotne wyprowadzenie Lanchestera (1908), który użył zasady zachowania energii i założenie, że ciąg silnika dokładnie anuluje opór. Na przykład, dla samolotu lecącego z prędkością 306 km/h = 85 m/s, przewidujemy okres fugoidy,  P ≈ 39, a dla v ~ 250 kt = 370 km/h = 103 m/s przewidujemy P ~ 47 s. Dla prędkości 150kt przewidujemy okres fugoidy 35 s, a przy 450 km/h przewidujemy P ≈ 57 s. Innym przykładem jest lot o prędkości rejsowej 500 mph = 435 kt = 805 km/h = 224 m/s gdzie klasycznie liczona fugoida ma okres 101.4 s. Porównajmy teraz te wyniki  z pełniejszymi nieraz obliczeniami modów oscylacji i z realnymi pomiarami w locie.

W książce "Dynamics of Flight" (2005) Etkin stosuje dużo pełniejszy zestaw równań dynamicznych, włączając tzw. pochodne aerodynamiczne i momenty bezwładności przykładowego samolotu pasażerskiego. Otrzymał dla v = 224 m/s następującą odpowiedź: P = 115 s; tłumienie zachodzi w charakterystycznym czasie ~3 okresów oscylacji. Szerszy zestaw równań Etkina przewiduje więcej wartości własnych, w tym szybko tłumione, krótkookresowe oscylacje, których my nie analizujemy. Nasze przewidywanie to okres P = 101.4 s, który jest o 12% krótszy. [Nawiasem mówiąc, wydanie książki z 2005 roku oparte jest na wydaniu z 1972 roku, w którym problem własności własnej został rozwiązany na starożytnym komputerze, w czasach, gdy komputery były tak rzadkie, że zasługiwało to na specjalną wzmiankę w książce; był to komputer klasy mainframe IBM 1130 na UTIAS - to nasz instytut badań lotniczych i kosmicznych UofT, którego Etkin był profesorem].

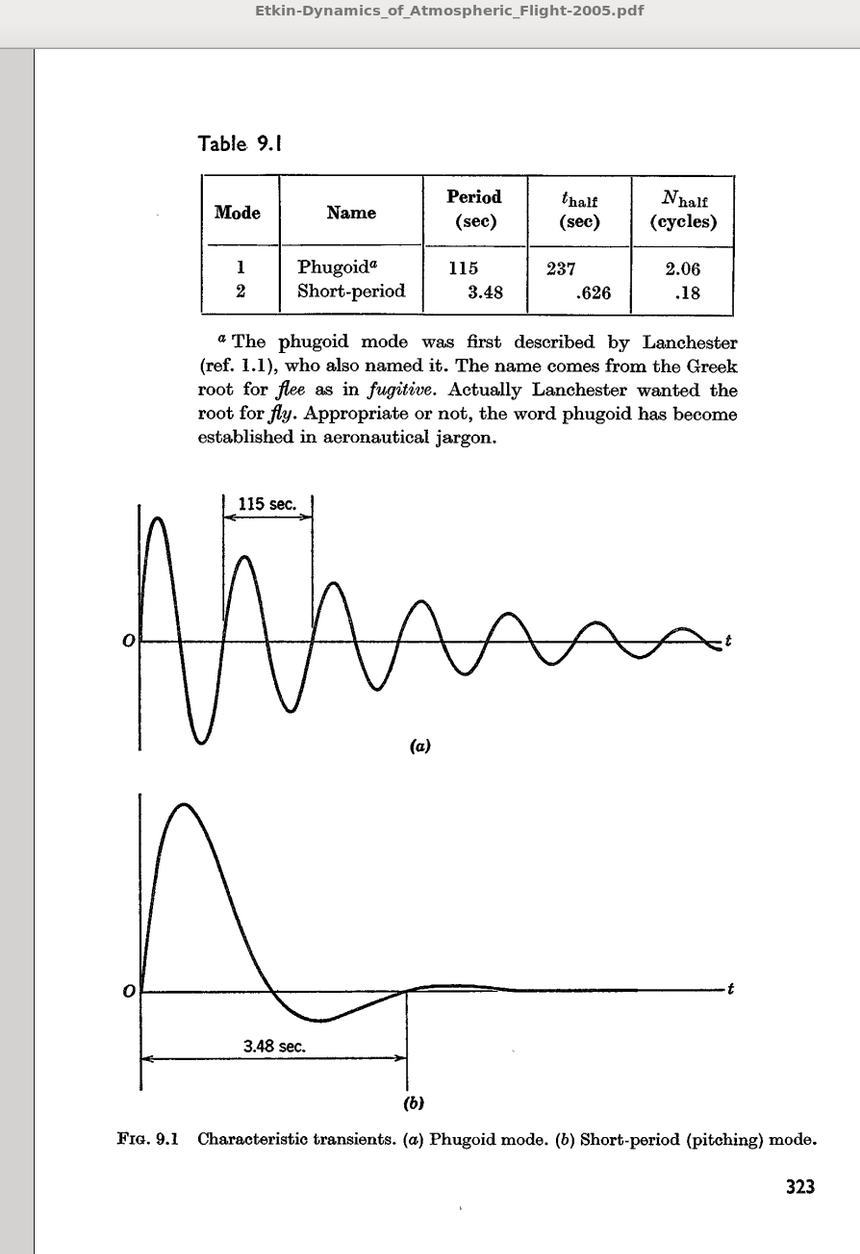
Rys. 1. Obliczenia modów długookresowego (fugoidalnego) i krotkookresowego zaburzeń stabilności podłużnej samolotu pasażerskiego (Etkin 2005).

Na rys.2a pokazany jest realny test w locie zaburzonym wychyleniem sterów przy v* = 150 kt, gdzie mały odrzutowiec oscylował z okresem około 50 s, podczas gdy my wyliczylibyśmy 35 s, wartość o 30% mniejszą. (Jak widać, prosta teoria nie zawsze dokładnie odpowiada mierzonym okresowościom!)

Wyprowadzenie robiące mniej założeń niż my, dyskutowane jest w książce o aerodynamice Cooke'a "Flight Dynamics Principles" (wyd. 2-gie, 2007) też zgadza się z naszym wynikiem z dokładnością jednej piątej wartości. Realne pomiary zobaczyć można na rysunku Cooke'a , z którego wzięliśmy poniższy rys.2a:

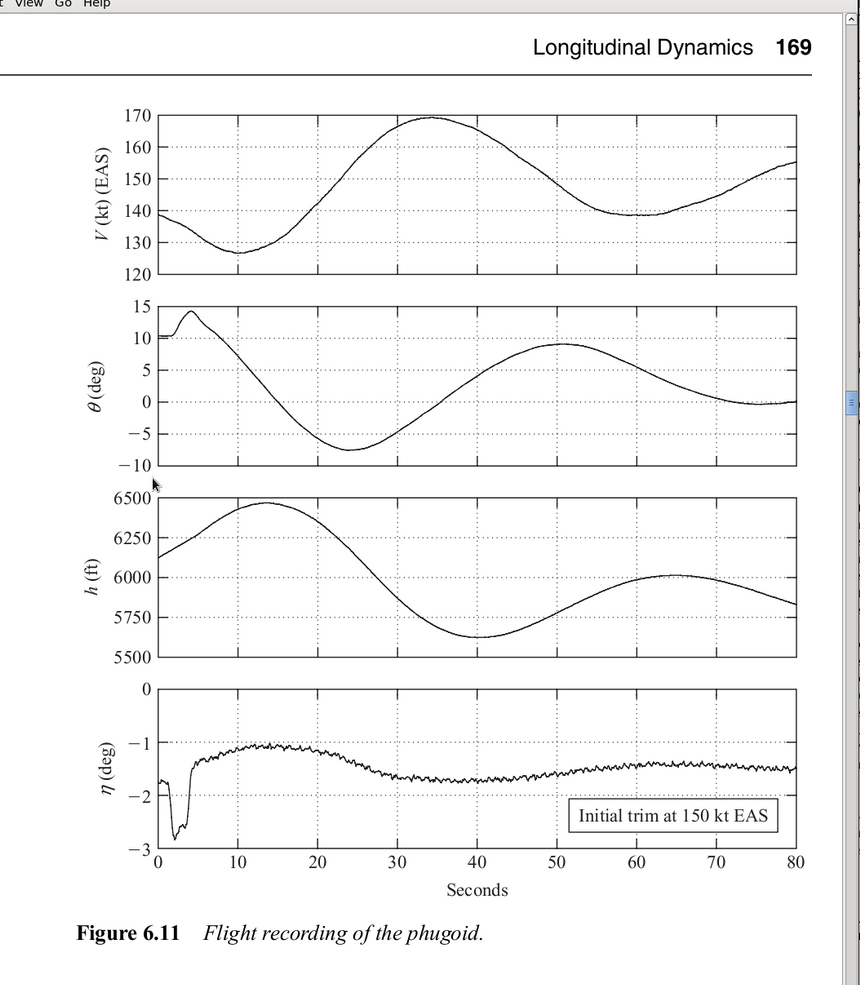
Rys. 2a. Pomiary zmian prędkości małego odrzutowca, kąta pochylenia w stopniach, wysokości w stopach, i kąta wychylenia sterów, w funkcji czasu. Odpowiedzią na chwilowe zaburzenie początkowe (wychylenie sterów) była fugoida o okresie P ~ 50 s.

Podobno już Żukowski liczył mody oscylacji podłużnych. Najstarszą pozycją literatury, do której dotarłem, jest książka Ostrosławskij i Kałaczew "Prodol'naja ustojcziwost'  i uprawliajemost' samoleta" (1951). Otrzymali oni o 20% dłuższy od klasycznej formuły Lanchestera okres fugoidy dla rozważanego przez nich modelu samolotu. Przy prędkości 450 km/h jak to widać z rys. 2b okres ten wynosi 72 s (w por. z  57 s prostej teorii), jak to widać z rys. 2b:

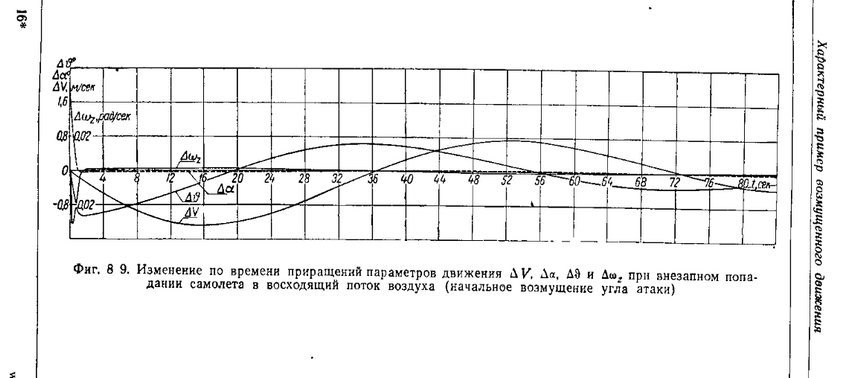
Rys. 2a. Modelowe obliczenie zaburzeń równowagi podłużnej w samolocie lecącym z prędkością 450 km/h (Ostroslawskij i Kalaczew 1951);  P = 72 s.

3.2. Znaczenie fugoidy

Mam nadzieję, że spodobała Ci się Czytelniku ta odrobina mechaniki lotu. Ma zastosowanie do samolotów wszelkiej wielkości, także sportowego RV-6, który uwielbia wchodzić w około 50-sekundowego okresu oscylację podłużną przy prędkości przelotowej (mój egzemplarz ma tylko autopilota kierunku/przechyłu). Możesz znaleźć w podręcznikach i na youtube wyjaśnienie innych rodzajów stabilności i związanych z nimi modów oscylacji, wszystkie są szybsze niż fugoida. Por. np.  https://www.youtube.com/watch?v=r3AFAQM7Ya0 .  

Dlaczego fugoidy są ważne? Ponieważ w przeciwieństwie do oscylacji krótkookresowych, długa wspinaczka i długie opadanie w fugoidzie powoduje duże odchylenie od początkowej trajektorii (wysokości). Śledzenie za tym efektem dodaje pracy pilotowi w sytuacji, gdy nie ma autopilota stabilizującego 'w kanale podłużnym', albo gdy musi go wyłączyć na zniżaniu końcowym (co nakazują instrukcje obsługi większości samolotów). Kapitan Sullenberger, który z powodzeniem wodował Airbusa 320 na rzece Hudson w Nowym Jorku po uderzeniu ptaka i utracie mocy silników, sugerował że automat zapobiegający oscylacjom fugoidalnym przeszkadzał mu zwiększać pochylenie samolotu tuż przed wodowaniem. Brzmi to trochę dziwnie, ale kto wie. 

3.3. Fugoida w Smoleńsku

Ostatnia rekonfiguracja klap i kąta statecznika nastąpiła ~2 pełne minuty przed końcem lotu. Czy na podejściu końcowym 10.04.10 wystąpiły związane z tym zaburzeniem równowagi lotu oscylacje podłużne, opisane powyżej? Pozostawię to pytanie bez odpowiedzi, żeby coś wam moi drodzy zostawić do roboty. Podejście, jak wiemy, było nieustabilizowane w sensie formalnym i praktycznie nie było przez większość ostatnich sekund sterowane efektywnie przez automat ciągu, gdyż ten zatrzymał się na ciągu minimalnym. Były wychylenia trymera wysokości (zmieniającego kąt natarcia), które znajdziecie bez trudu w raportach MAK i KBWLLP.

Wystąpiła gasnąca oscylacja prędkości pionowej (bez przechyłu) o długim okresie rzędu ~30 sekund.  Nasza prosta teoria daje P ~ 35 s przy prędkości 78 m/s = 280 km/h. Zgodność jest niezła; dużo lepszej nie uzyskuje się w realnych testach przy użyciu nawet bardziej skomplikowanych obliczeń. 

Idźmy dalej. Jak szybko,  wg przedstawionej teorii, następuje tłumienie fugoidy? Wzrasta ono, kiedy samolot zmienia konfigurację wysuwając klapy i zmniejszając L/D dajmy na to z 17 do 6 (jak w tupolewie z jego konfiguracją do lądowania). Wtedy, zgodnie z teorią, e-krotne tłumienie amplitudy powinno zająć τ~0.9 okresów oscylacji. I tyle mniej więcej zajęło (por. rys. 3), gdyż każdy następne wahnięcie jest ok. dwukrotnie mniejsze  (chociaż nie e-krotnie, więc może τ~1.4 P na rysunku?). 

A więc fugoida czy nie? Chętnie usłyszę w dyskusji. 

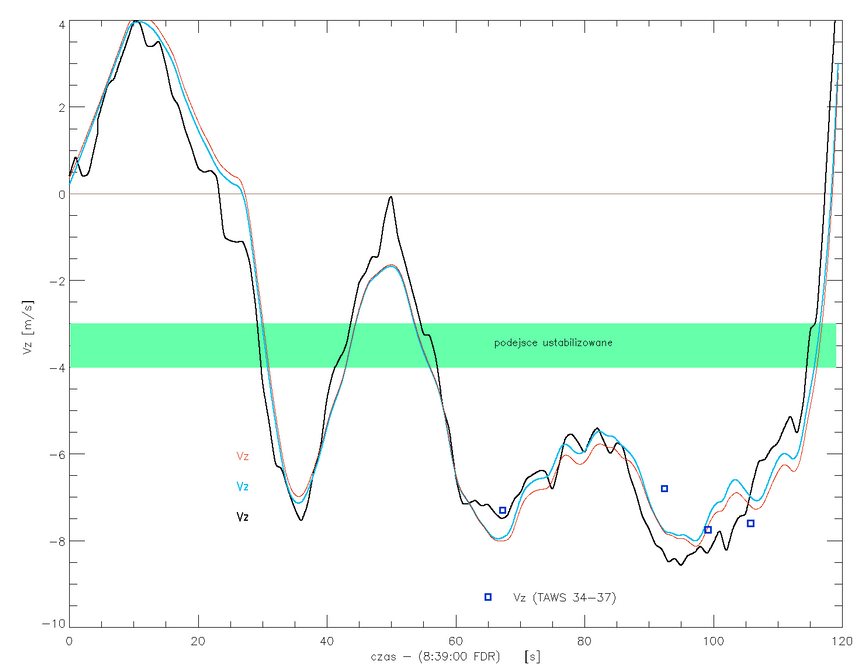 Rysunki 3 i 4, pokazujące Vz(t) i trajektorię PLF 101.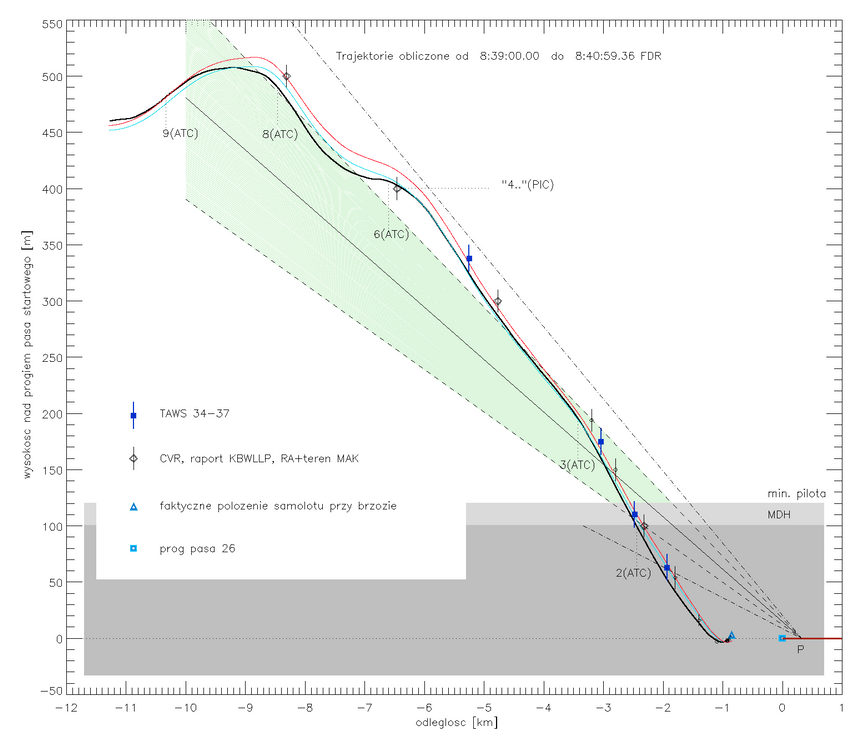

Niezależnie od tego skąd wzięły się pokazane tu oscylacje prędkości pionowej tupolewa rządowego, położone były bardzo pechowo w czasie. Gdy samolot zbliżał się do minimalnej wysokości zniżania, na wysokości ok. 180 m, w odległości ~3.2 km od progu pasa, nastąpiła faza zwiększenia tempa opadania  Vz od około  -6 m/s do około -8.5 m/s, w związku z czym nachylenie trajektorii zmieniło się z takiego, które doprowadziłoby samolot po linii prostej na odległość 200-300 m od początku pasa, czyli prawie na pas startowy, do takiego nachylenia, które celowało w okolicę radiolatarni BRL, o cały kilometr wcześniej. Warto więc może zastanowić się czy oscylacje głównie związane były z fugoidą, czy z trymowaniem steru wysokości przez pilotów. Czy fatalne w skutkach zwiększenie i tak za dużej prędkości i kąta opadania w końcówce lotu, w chmurze, było świadomym działaniem pilotów czy kombinacją ich za szybkiego zniżania i dodatkowej fugoidy.  Odpowiedź na to pytanie nie zmieni przyczyn katastrofy, może jednak dopowie pewne jej okoliczności. 

(c) Paweł Artymowicz 

9 kwietnia 2019 r.