Dlaczego wynik doświadczenia Michelsona-Morleya jest oczywisty?

Link do poprzedniej notki

Znany paradoks c-v=c oznacza, że światło dotrze do obserwatora zawsze z prędkością c (w próżni), choćby ten oddalał się od źródła z dowolnie dużą prędkością v.

Taki zapis stanowi pewien problem dość zaskakujący i kłopotliwy. Aby rozwiązać go zgodnie z Teorią Względności trzeba (mówiąc w uproszczeniu) „zakrzywić przestrzeń” za pomocą transformacji Lorentza, bo tylko wtedy rachunki w tym osobliwym równaniu będą się zgadzały. A czy można wyjaśnić to zjawisko na podstawie klasycznej geometrii z płaską przestrzenią euklidesową bez jej zakrzywiania? Na pierwszy rzut oka wydaje się to niemożliwe. No chyba, że spojrzymy na zagadnienie najprościej, jak się da i zadamy odważne pytanie: A jak to można wytłumaczyć logicznie?

No cóż… Okazuje się, że wszelkie pozorne paradoksy związane z Transformacją Lorentza (i znane z Teorii Względności) znikają, jeśli przyjmiemy następujący postulat:

Foton porusza się miedzy nadajnikiem a odbiornikiem w ośrodku rozpiętym na wzór nieskończenie rozciągliwej i nieważkiej gumki. Możemy ten ośrodek nazwać próżnią, eterem albo ze względu na jego nieważkość po prostu właściwością przestrzeni.

Dlaczego paradoksy znikają? Omawialiśmy to dość szeroko w poprzednich notkach, starając się przy tym nie interpretować faktów, a jedynie pokazać obiektywne konsekwencje powyższego założenia bez „machania rękami”,  korzystając ze ścisłych matematycznych zależności.

Było dla mnie dość niezwykłym odkryciem, ze wspomniany postulat działa jak klucz sprowadzający paradoksy Teorii Względności do zupełnie zwykłych oczywistości, gdzie dylatacja czasu i kontrakcja odcinka znajdują naturalne, klasyczne wyjaśnienie

Więcej, okazało się, że prezentowany model ruchu ma charakter uniwersalny, który wyjaśnia zarówno zjawiska relatywistyczne, jak też kosmologiczne czy związane z oddziaływaniem grawitacyjnym. Przyroda jest przecież jedna, dlatego taka unifikacja była oczekiwana, a nawet powiedziałbym wymagana. Mówimy, że istnieje redshift relatywistyczny (dopplerowski), kosmologiczny i grawitacyjny – nasz model pokazuje, że wszystko to jest jednym zjawiskiem.

I. Zacznijmy od redshiftu dopplerowskiego.

Przede wszystkim przypomnijmy (po dłuższej przerwie) formułę ruchu wynikającą z przyjętego postulatu. Jak pamiętamy, składa się ona z dwóch równań.

No to obliczmy ten redshift dopplerowski z.

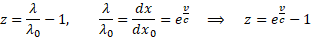
Oto relatywistyczny redshift Dopplera. Na marginesie dodajmy, że ten sam wzór wyrażony za pomocą prędkości Lorentza v_L przyjmuje dobrze znaną, równoważną postać.

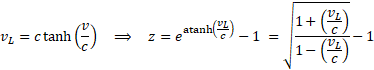
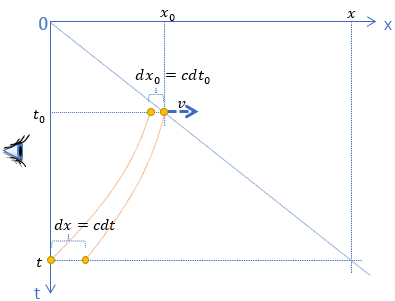
Postać redshiftu z w funkcji v nie jest sama w sobie żadnym okryciem ale (jak inne opisywane wcześniej zjawiska) zwykłą matematyczną konsekwencją przyjętego postulatu. Prosty model ruchu omawianych zjawisk przedstawiony jest na poniższym rysunku.

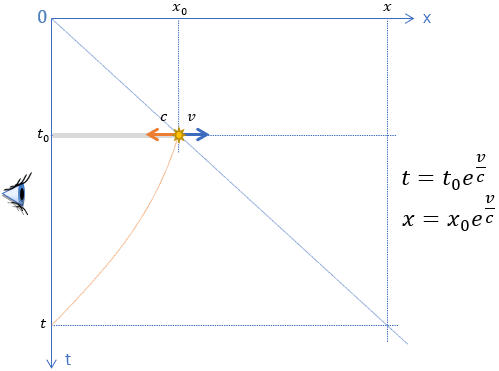
Źródło promieniowania oddala się z prędkością v. Z nieskomplikowanych obliczeń (pełne wyprowadzenie tutaj) wynika, że sygnał wyemitowany w chwili t₀ dotrze do obserwatora w chwili t, natomiast cząstka oddali się w tym czasie z punktu x₀ do x.

A co do tego ma tytułowe doświadczenie Michelsona-Morleya? Spójrzmy na rysunek. Zauważymy, że fala EM w naszym modelu oderwie się od cząstki zawsze z prędkością c oraz dotrze do obserwatora także zawsze z prędkością c. I oto mamy – jakże prozaiczne – wytłumaczenie wspomnianej na wstępie tajemniczej równości c-v=c. A wszystko dlatego, że brzegi ośrodka, w którym porusza się foton (zgodnie z naszym postulatem) są w zrozumiały sposób zawsze nieruchome odpowiednio względem nadajnika i odbiornika.

Jak wiemy, celem doświadczenia Michelsona-Morleya było wykrycie „wiatru eteru”. Uzyskano wynik, który jest dowodem jednej z dwóch hipotez:

• Eter nie istnieje,
• Eter istnieje, ale jest nieruchomy względem interferometru.

Zauważmy, że opisywany postulat jest wręcz wytłumaczeniem, dlaczego Michelson nie mógł wykryć „wiatru eteru”. Po prostu wiatr nie wieje, jeśli jest nieruchomy względem obserwatora. Tak, jak koniec gumki zawsze jest nieruchomy względem punktu zaczepienia. No i mamy odpowiedź, dlaczego wynik tego doświadczenia był oczywisty.

II. A teraz przejdźmy do redshiftu kosmologicznego.

Jak wspomnieliśmy przyroda jest jedna i także nasz model ruchu dla obu przypadków też jest jeden. W kosmologii wyrażenie x/x₀=R to po prostu tzw. współczynnik skali, znany z równań Friedmana opisujących najpopularniejszy model ewolucji wszechświata. Współczynnik skali R znormalizujmy tak, żeby w chwili „teraz” t₀ równał się R(t₀ )=1. W efekcie otrzymamy tę samą formułę ruchu, co poprzednio tylko inaczej nazwaną. 

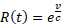
Współczynnik skali mówi ile razy powiększył się wszechświat od momentu emisji fotonu do chwili jego dotarcia do obserwatora (jak widzimy nie ma tu problemów związanych z jednoczesnością zdarzeń, chociaż punkty x₀ i x są oddalone w czasie i przestrzeni).

Temat związany w ekspansją wszechświata jest rozległy i leży poza zakresem notki, tutaj tylko wspominamy o wybranych zagadnieniach. Zobaczmy, jak przy użyciu naszego modelu można wyprowadzić prawo Hubble’a.

W poniższym wzorze R z kropką oznacza pochodną czynnika skali, a H jest parametrem Hubble’a:

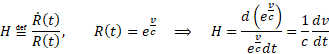
Korzystając ze wzorów Modelu Naturalnego napiszemy dalej:

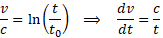
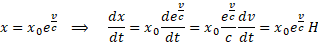
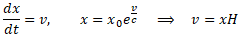
I oto uzyskaliśmy wzór opisujący leżące u podstaw kosmologii prawo Hubble’a, gdzie v jest prędkością oddalania się galaktyki, a x jest jej aktualną odległością od nas w chwili „teraz”. Zakładając stałą prędkość v, możemy oszacować wiek wszechświata, jako odwrotność parametru Hubble’a (t=1/H).

Ale co z tym redshiftem w kosmologii? W naszym modelu jest on tym samym zjawiskiem, co redshift dopplerowski i wyraża się takim samym wzorem.

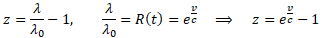
W szczególności dla bliskich galaktyk redshift kosmologiczny przybiera uproszoną postać z=v/c. Skąd się bierze to uproszczenie? Wynika ono z małych prędkości recesji tych galaktyk. Jest to po prostu przybliżenie ogólnych wzorów naszego modelu dla małych prędkości.

Względnie znikoma prędkość ucieczki bliskich galaktyk (chodzi o prędkość wynikającą z rozszerzania się wszechświata) pozwala uwzględnić tylko pierwsze dwa człony rozwinięcia funkcji ekspotencjalnej w szereg. W efekcie uzyskujemy szukany wynik.

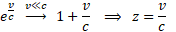
Wspomniana unifikacja powoduje, że niepotrzebny jest podział na różne definicje prędkości w kosmosie. Dotąd mieliśmy prędkość v, z którą rozszerza się wszechświat i ta prędkość zgodnie z zasadami kosmologii może przekraczać prędkość światła c oraz prędkość v_L niezależną od ekspansji kosmosu i ta prędkość nie może przekroczyć c. Był to pewien kłopot, który wymagał założenia, że v większa od c wyjątkowo nie przeczy Teorii Względności bo wynika z ekspansji wszechświata, co było zabiegiem dość rozpaczliwym. Przyjęcie naszego postulatu powoduje, że zarówno zjawiska kosmologiczne, jak relatywistyczne opierają się na tym samym modelu ruchu i mogą być opisane za pomocą jednej faktycznej prędkości v.

Właściwie powyższe wskazanie na uniwersalność prezentowanego modelu, to dobry moment na zakończenie notki, ale chcę w tym kontekście wspomnieć jeszcze o dwóch aspektach.

Pierwszy aspekt, czyli o niezwykłości współczynnika skali.

W poprzedniej notce rozpatrywaliśmy dwa kolejne grzbiety fali EM. Wróćmy tego modelu.

Cząstka porusza się z prędkością v i emituje falę EM o długości dx₀ i okresie dt₀. Na rysunku żółtymi kropkami zaznaczono dwa kolejne grzbiety tej fali. Obliczmy w jakich w odstępach czasu oba grzbiety dotrą do celu.

Poniższa proporcja nie zależy od toru ruchu cząstki i wynika wyłącznie z położenia punktów x₀, x. 

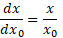
Wiedząc, że grzbiety fali EM zawsze startują i docierają do celu z prędkością c, napiszemy:

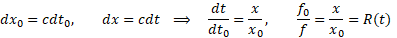
Otrzymaliśmy niezwykłą zależność. Dlaczego niezwykłą? Bo znając odległość x₀ od cząstki w momencie emisji fali i mierząc częstotliwość docierającego sygnału f jesteśmy w stanie stwierdzić w jakiej odległości x znajduje się źródło promieniowania obecnie w danej chwili jednoczesności (x =x₀f₀/f), choćby było oddalone i miliardy lat świetlnych. Można powiedzieć, że w pewnym sensie informacja o położeniu cząstki jest dostępna dla nas natychmiast, docierając z nieskończenie dużą prędkością, a wynika to po prostu z właściwości przestrzeni.

Drugi aspekt, czyli skąd wiemy, że ekspansja wszechświata przyśpiesza?

Dokładne oszacowanie odległości do dalekich obiektów jest jednym z większych wyzwań kosmologii, niemniej potrafimy dokonać takiej oceny choćby poprzez obserwacje jasności tzw. „świec standardowych”. I tutaj następuje niespodzianka. Okazuje się, odległe supernowe wydają się być dalej, niż wynikałoby to z ich redshiftu. Wytłumaczeniem tego faktu jest wniosek, że wszechświat przyśpiesza. Oczywiste, prawda?

Chyba jednak nie jest to takie oczywiste. Przecież obserwowany obraz supernowej pochodzi sprzed miliardów lat – można by pomyśleć, że to właśnie wtedy wszechświat przyśpieszał, a teraz zwalnia.

Jak jest naprawdę i dlaczego? Rozstrzygniecie dylematu wynika ze szczegółowych modeli kosmologicznych wywodzonych z równań Einsteina. My jednak pokażemy, jak jasno przyśpieszoną ekspansję wszechświata tłumaczy nasz model oparty na przyjętym postulacie. Cały proces możemy wręcz narysować.

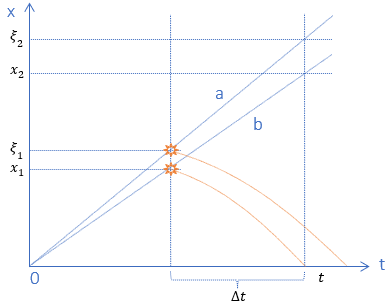
Punkt 0 to początek istnienia wszechświata. Proste a, b ilustrują prawo Hubble’. Załóżmy, że światło z odległej gwiazdy dociera do nas w chwili „teraz” t. Pomiar redshiftu pozwala obliczyć jak bardzo rozszerzył się wszechświat od emisji sygnału (w chwili t-Δt).

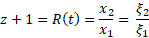
Uzyskana proporcja mówi tyle, że jeśli sygnał został wyemitowany w odległości x₁ od nas, to obecnie źródło promieniowania znajduje się w odległości x2. Ale jeśli sygnał został wyemitowany w odległości ξ1, to teraz źródło znajduje się w odległości ξ2. Który z tych ilorazów jest właściwy dla naszego sygnału?

Zauważmy, że powyższy model wyklucza możliwość wygenerowania sygnału w odległości ξ1, ponieważ wtedy fala nie zdążyłaby dotrzeć do nas w chwili t. I tu pojawia się niespodzianka, o której pisałem. Pomiar jasności wskazuje, że w momencie emisji sygnału gwiazda znajdowała się właśnie w odległości ξ1. Jak to rozumieć i dlaczego oznacza to przyspieszoną ekspansję wszechświata?

Zagadkę tłumaczy poniższy rysunek.

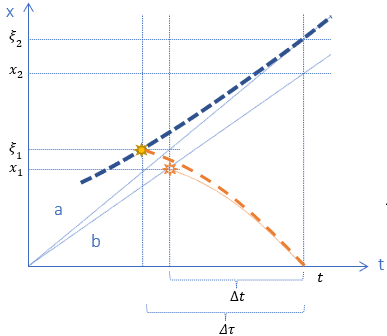
W chwili „teraz” krzywa ekspansji wszechświata musi być zgodna z prawem Huble’a, czyli musi przylegać do prostej a. A zatem nie ma innej możliwości geometrycznego wytłumaczenia zjawiska, jak przyjęcie, że sygnał został wyemitowany wcześniej i stąd krzywa rozszerzania się wszechświata musi mieć kształt podobny do tego na rysunku, co oznacza przyspieszoną ekspansję. Dlatego też zmierzona odległość luminacji ξ_L jest większa, niż oczekiwana x_L. 

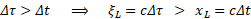
Podkreślmy jeszcze raz to, co było istotą naszych rozważań. Pokazaliśmy, że zarówno wzory relatywistyczne, jak kosmologiczne wynikają z jednego i tego samego modelu ruchu, jeśli tylko przyjmiemy wspomniany na wstępie postulat. Przyroda jest jedna i czy to w skali laboratorium, czy w skali rozszerzającego się kosmosu obowiązuje ta sama zasada ruchu.

W szczególności omawiany postulat jasno tłumaczy zależności ruchu w polu grawitacyjnym. Ale o tym dość szczegółowo powiemy już w dalszej części.