Dzisiejsza opowieść to historia pełna zaskakujących zwrotów akcji, wybuchów i strzelanin, z udziałem tajnych agentów, złoczyńców i stróżów prawa, o której pisały gazety całego świata. Żartowałem. Mało kto o niej pisał i wiedział, ale jej ciężar gatunkowy rzeczywiście był wielki.
W kilku notkach (o liczbach wymiernych, rzeczywistych i naturalnych) pisałem o zgrzytach między materialną rzeczywistością a ścisłą matematyką, choć nie da się ukryć, że matematyka powstawała jako narzędzie do policzenia i zmierzenia kawałków owej rzeczywistości. Robiła to nad wyraz skutecznie, jednak w pewnym momencie niebezpiecznie zaczęła pasować do cytatu z bezimiennego mistyka zacytowanego przez detektywa Wilhelma: Porządek, jaki nasz umysł wymyśla sobie, jest niby sieć albo drabina, którą buduje się, by czegoś dosięgnąć. Ale potem trzeba drabinę odrzucić, gdyż dostrzega się, że choć służyła, była pozbawiona sensu. Można się domyślić, że opisywany przeze mnie ostatnio przykład z planetami raczej nie wstrząsnął społecznością matematyków. Strzał przyszedł z innej strony.
Teoria mnogości
Zbiory są łatwe – policzyć sumę zbiorów czy różnicę, a nawet część wspólną – to były najfajniejsze lekcje na matematyce. Skąd brać zbiory? Zewsząd! A co to jest zbiór? Też pytanie: jaki jest zbiór każdy widzi. Co tam można definiować? Zbieramy jakieś obiekty (elementy) do kupy i już mamy zbiór. Kiedy stało się jasne, że liczby naturalne (służą do konstrukcji innych liczb), to pewne własności zbiorów skończonych, nauka o zbiorach czyli teoria mnogości stała się fundamentalną dla matematyki.
Osobą, która położyła największe zasługi w tej dziedzinie był matematyk G. Cantor. W wielu miejscach można sobie poczytać o jego prostych, efektownych i przekonujących dowodach dotyczących zbiorów liczbowych. Niektóre twierdzenia przy pierwszym czytaniu zdawały się szokujące: odcinek ma tyle samo punktów, co cała trójwymiarowa przestrzeń. Dziwne, ale prawdziwe. Jedno z jego twierdzeń dotyczyło tzw. zbioru potęgowego. Co to jest? Zbiór podzbiorów danego zbioru. Zobaczmy na obrazek:
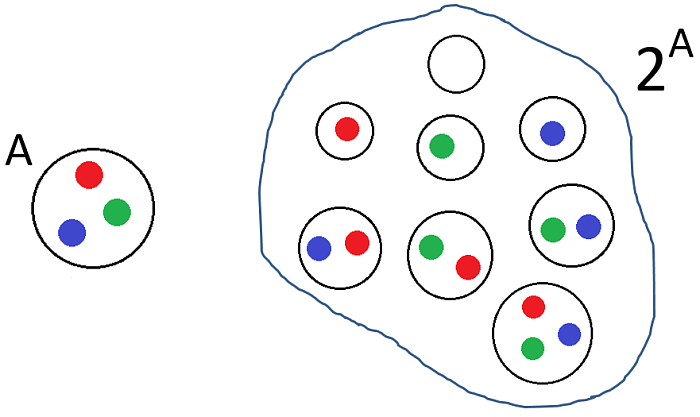
Zbiór A ma trzy elementy. Po prawej stronie narysowałem wszystkie podzbiory A: trzy zbiory jednoelementowe, trzy dwuelementowe, sam zbiór A (każdy zbiór jest swoim podzbiorem) i zbiór pusty. W sumie osiem elementów czyli 23. No i okazuje się, że jeśli jakiś zbiór ma n elementów, to da się z niego utworzyć 2n podzbiorów. Dlatego na zbiór podzbiorów zbioru A stosuje się zapis 2A i nazywa zbiorem potęgowym.
Twierdzenie o którym wspomniałem mówi, że 2A ma zawsze więcej elementów niż A. Obowiązuje ono również dla zbiorów nieskończonych, co będzie miało istotne konsekwencje.
Jest rok 1899. Koniec wieku. Na arenę wchodzi zbiór wszystkich zbiorów. Oznaczmy go symbolem Ω. Definicja jest prosta – jeśli X jest zbiorem, to jest również elementem Ω. Jak mamy Ω, to popatrzmy teraz na zbiór jego podzbiorów, czyli zbiór potęgowy 2Ω. Z jednej strony ma więcej elementów niż Ω, bo tak jest dla każdego zbioru potęgowego. Z drugiej strony elementami 2Ω są podzbiory czyli również zbiory, a więc na pewno należą do Ω. Czyli zbiór 2Ω zawiera się w Ω a jednocześnie jest od niego liczniejszy.
Czyli sprzeczność.
W tym czasie w omawianym obszarze odkryto tych sprzeczności więcej. Najprościej byłoby wyrzucić teorię mnogości do kosza (i być może wtedy była to dość powszechna opina), tym bardziej, że kłopotliwe paradoksy nie występowały gdzie indziej. Mimo to zorientowano się, że dziewiętnastowieczna matematyka da się sprowadzić właśnie do nauki o zbiorach. Kto zapewni, że zło nie objawi się jakimiś sprzecznościami w algebrze czy analizie? Skoro fundament się chwieje, to co z resztą gmachu? Czyżby miał runąć? Kryzys na całego.

Zanim opowiem, jak wyleczono królową nauk, dwa argumenty, niekoniecznie matematyczne, że mimo wszystko należało się spodziewać szczęśliwego zakończenia. Po pierwsze skoro zbudowano tyle ogromnych dziedzin matematyki i pasują one do siebie, działają i do tej pory nie zaskoczyły jakimiś niespodziankami, to mało prawdopodobne, żeby okazały się złe. Czyli drogi uczniu, który cierpisz przed sprawdzianem z matmy – paradoksy cię nie uratują, będziesz musiał kuć. Po drugie podobne rzeczy już się zdarzały: Pitagorejczycy też doszli do sprzeczności w swojej nauce, kiedy odkryli, że przekątna kwadratu nie jest ułamkiem. Co wtedy zrobili? Zamiast wyrzucić całą swoją wiedzę do kosza, musieli ją poprawić, choć przyszło im to z trudem.
No to zobaczmy, jak poprawiono zbiory.
Na początku był ∅
W początkowych latach XX wieku zaistniała w środowisku intensywna dyskusja filozoficzno-matematyczna co z tym fantem zrobić, której nawet nie podejmuję się streszczać. Skupię się nad tym, co konkretnie zrobiono. Ponieważ pojęcie zbioru jest ciężkie do zdefiniowania, założono kilka jego własności, co do których uznano, że są akceptowalne i będą stanowić podstawę do dalszych prac. Czyli ustalono listę aksjomatów, z których ma się korzystać przy dowodzeniu twierdzeń i definiowaniu nowych obiektów matematycznych. Pracę o podobnych charakterze wieki wcześniej wykonał Euklides, który zaproponował zestaw aksjomatów, pasujących do geometrii wymyślonej (odkrytej?) przez jego poprzedników.
Aksjomaty pochodzą od E. Zermelo (rozpoczął w 1904) i A. Fraenkela (zakończył w latach 30-tych). Rzecz jasna w robotę zaangażowanych było więcej ludzi - choćby nasz W. Sierpiński. Jednym z uczonych, który tę pracę wykonywał, był również polski matematyk Z. Kuratowski. Zajrzyjmy do książki „Wstęp do teorii mnogości”, której był współautorem wraz z A. Mostowskim:

W oparciu o wypisane aksjomaty zbudujmy pierwszy zbiór. Skoro istnieje co najmniej jeden zbiór A, to obliczmy sobie różnicę:
∅ = A – A
Wynik to nic innego jak zbiór pusty. Zbiór nie zawierający żadnych elementów. Ponieważ dobór aksjomatów może być nieco inny (chodzi o to, żeby produkowały to samo), czasami istnienie zbioru pustego po prostu się postuluje. Tak czy siak mamy konkretny, istniejący zbiór ∅. Ten zbiór to liczba 0.
Kolejny zbiór jaki skonstruujemy, to zbiór zawierający zbiór pusty jako element. Ten zbiór będzie liczbą 1:
1 = { ∅ }
Mogłoby się wydawać, że to te same zbiory, ale tak nie jest, bo przecież zbiór pusty ma 0 elementów, a zbiór 1 ma jeden element (odpuszczę sobie porcję wiedzy do wykonania, która w ogóle pozwoliłaby nam na użycie sformułowania „zbiór ma … elementów”). Kolejny krok, to zbiór 2:
2 = { ∅, {∅} }
i kolejne liczby:
3 = { ∅, {∅}, {∅, {∅}} }
4 = { ∅, {∅}, {∅, {∅}}, {∅, {∅}, {∅, {∅}}} }
i tak dalej…
Inaczej można to zapisać:
0 = ∅
1 = { 0 }
2 = { 0, 1 }
3 = { 0, 1, 2 }
4 = { 0, 1, 2, 3 }
i tak dalej…
Pominę tu wiele szczegółów kuchni teoriomnogościowej czy ogólnie matematycznej, dzięki której te twory zostaną zmuszone do zwykłego działania czyli dodawania, odejmowania czy zliczania elementów innych zbiorów. W ten sposób zbudujemy dowolną liczbę naturalną, ale zbioru liczb naturalnych nie zrobimy. Żeby go mieć trzeba by pociągnąć procedurę tworzenia liczb do nieskończoności. Dlatego w kolejnym aksjomacie musimy sobie na to pozwolić.
Aksjomat o nieskończoności u Kuratowskiego ma numer VII, bo po drodze kilka innych było potrzebnych do różnych celów o których akurat nie piszę. Nie ma co przytaczać jego brzmienia, bo nie jest ono zbyt proste. Jego sens jest jednak w miarę jasny: Postulujemy istnienie zbioru do którego należą dowolne zbiory wygenerowane w powyższy sposób. Czyli pozwalamy sobie na istnienie zbioru:
N = { 0, 1, 2, 3, 4… }
Uff… No to mamy liczby naturalne. Teraz można zrobić z nich inne zbiory. Na przykład ułamki czy liczby rzeczywiste, no a z nich resztę matematyki. Rzecz jasna wcześniej trzeba udowodnić, że zaproponowane aksjomaty nie są ze sobą sprzeczne. A ponieważ to zrobiono, to jednak się nie zawali :)
W ten sposób dostaliśmy matematykę, która pozbawiona jest sprzeczności. Odbyło się to jednak kosztem oderwania się od rzeczywistości. Nie znajdziemy w niej zbiorów gruszek, uczniów i planet. Z drugiej strony wyrzucono też wszelkie „niedodefiniowane zbiory” o charakterze mocno abstrakcyjnym. Na przykład te, których elementy określano za pomocą jakiejś własności. Poniżej mamy zapis mówiący, że do A należą obiekty mające daną cechę:
A = { x: x ma taką a siaką cechę }
Wypisując coś takiego nie martwimy się jakie konkretnie będą to elementy. Bo wszystko co pasuje, będzie brane pod uwagę. Wszystko, czyli tak naprawdę nie wiadomo co. Takie postępowanie zostało zarzucone i teraz jeden z postulatów pozwala na używanie podobnej konstrukcji, ale tylko do tworzenia podzbiorów z istniejących już zbiorów:
A = { x∈B: x ma taką a siaką cechę }
Powyższe zadziała, jeśli wcześniej skonstruowaliśmy B. To dlatego poprawiona teoria mnogości, a wraz z nią cała matematyka, nie boi się już paradoksu wszystkich zbiorów.
Uwagi końcowe:
- Opisany w notce sposób na skonstruowanie zbioru liczb naturalnych na podstawie aksjomatów teorii mnogości nie jest jedyny. Są inne, ale ten wymyślony przez J. v. Neumanna, jest chyba najbardziej lubiany.
- Zapewne gdyby ktoś chciał opowiedzieć swoją historię o teorii mnogości mógłby inaczej porozkładać akcenty czy wspomnieć o zagadnieniach, które lekką ręką pominąłem.
- I już całkiem na koniec (moja) refleksja: Rewolucja teoriomnogościowa odmieniła praktykę stosowania matematyki – coraz trudniej mówić o funkcji, nie wspominając o jej dziedzinie. Choć powiem wam w tajemnicy, że fizykom zdarza się to do dziś.







Komentarze
Pokaż komentarze (82)