W wersji pierwotnej notka niniejsza, w której to notce występują dwie hiperbole, zaczynała się od przytoczeniem początku z dawnej notki o parabolach .
A w tej dawnej notce o parabolach był fragment mojej uniesionej poezji gdy stawiałem pierwsze kroki na drodze fizyka-teoretyka. Tak się to zaczynało:
Ruszę jak huragan jak burza
Moim hobby jest szybkość
Ruszę w grzmocie potężnym
zamyślenia.
Oto już. Oto ruszam. Z rosnącym przyśpieszeniem
Ruszyłem p ę d z ę na wprost
oszalały świat
W notce niniejszej przyśpieszenie (własne, odczuwalne) jednak nie rośnie, jest stałe. To prędkość za to rośnie. Jak w tym koncercie fortepianowym Mozrta z Barenboimem jako dyrygentem i pianistą:
Pisałem najpierw o paradoksie bliźniąt. Paradoks bliźniąt nie jest paradoksem, jest opisem zjawiska. W poprzedniej notce opisałem krótko paradoks dwóch statków kosmicznych Bella-Einsteina. To także opis pewnego zjawiska. Nić łącząca dwa przyśpieszające i poruszające się zawsze z tą sama prędkością i w tym samym kierunku statki pęka, bowiem statki te, choć z jednej strony pozostają w stałej odległości od siebie, z drugiej, ważniejszej, strony, się od siebie oddalają. Aby się od siebie nie oddalać, należy zrobić coś więcej niż pozostawać w stałej odległości. Należy się do siebie zbliżać.
Dziś tego zbliżania szczegóły. Notka dzisiejsza jest jedynie wstępem, preludium. Urwie się w połowie. I ciąg dalszy nastąpi.
Jak należy się do siebie zbliżać by tworzyć układ trwały, stabilny, solidny układ odniesienia poruszający się ruchem przyśpieszonym pomimo tego, że w teorii względności pojęcie ciała sztywnego nie istnieje? Notka dzisiejsza jest wstępem do odpowiedzi na to pytanie.
Zacznę od przypomnienia „paradoksu Bella” z poprzedniej notki przywołując zamieszczoną tam ilustrację.
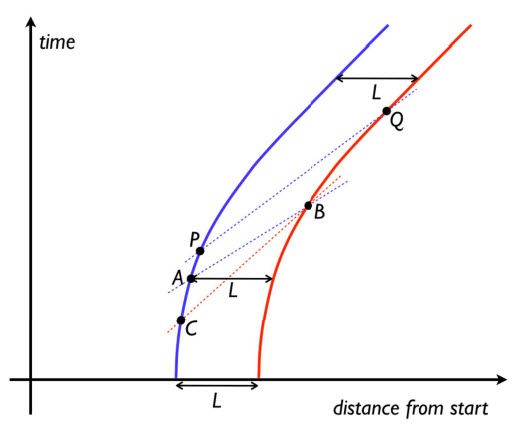
Opuszczamy tu wymiary Y i Z w których nic interesującego się nie dzieje. Z wymiarów przestrzennych zostawiamy jedynie X - oznaczone jako X1. Oba statki poruszają się w dodatnim kierunku osi X – to oś pozioma. Oś pionowa to oś czasu, ścislej, oś X0=cT, gdzie c jest prędkością światła. Oba statki startują w chwil T=0, zaczynając od prędkości 0 i jednostajnie identycznie przyśpieszając. Wykresy historii (linii świata) ich ruchu przedstawione na ilustracji mają identyczny kształt, tylko ten niebieski, przedstawiający rakietę pozostającą w tyle, jest przesunięty w stosunku do lidera, tego czerwonego, przesunięty wstecz o stałą odległość L jeśli mierzyć w spoczywającym inercjalnym układzie odniesienia.
Na ilustracji widać także linie przerywane łączące dwa statki. Te linie są ważne i notkę dzisiejszą i następną poświęcam omówieniu tych linii. Będą wzory, należy zatem zapiąć pasy.
Oto formuły opisujące historie obydwu statków kosmicznych

Parametr a, ten sam dla obu statków, to „przyśpieszenie własne odczuwane”, tzn. odczuwane jako siła przyciskająca do dna pasażerów obu statków. Nie będziemy wchodzić w definicję tego pojęcia, nie o tym ta notka.
Zajmijmy się najpierw linią czerwoną, oraz liniami AB i PQ.. Choć tego może na pierwszy rzut oka nie widać, obie linie przechodzą przez początek układu współrzędnych. Co to za linie i skąd się biorą?
Są to linie jednoczesności obserwatora związanego ze statkiem liderem. Jak? Skąd? Dlaczego?
Przyjmijmy dla uproszczenia, że pracujemy w układzie jednostek w którym prędkość światła c jest liczbowo równa jedności. Na wykresie (X,T) wektor styczny do linii świata to wektor prędkości, ściślej „czteroprędkości”, a w naszym przypadku, ponieważ opuściliśmy Y i Z, to wektor dwuprędkości, ale będę go nazywał wektorem czteroprędkości.
Możemy go wyliczyć w postaci jawnej z naszej formuły. Przy tym wynik będzie ten sam dla obu linii, bowiem jedna jest jedynie przesunięciem drugiej. Składowe wektora stycznego, oznaczymy go symbolem u, obliczamy różniczkując współrzędne po czasie, w naszym przypadku po czasie własnym. Będzie więc to wektor prędkości własnej.

Ten fakt że kwadrat długości tego wektora jest równy -1 związany jest z tym, że parametrem na trajektorii jest właśnie czas własny. Jest to własność charakteryzująca jednoznacznie czas własny, ale nie to jest przedmiotem naszych rozważań.
Składowe wektora czteroprzyśpieszenia (własnego) otrzymujemy obliczając pochodne czterowektora prędkości po czasie (własnym).

Z faktu, że kwadrat długości (w sensie Minkowskiego) wektora prędkości jest stały wynika, że wektor czteroprzyśpieszenia, nazwiemy go w, jest prostopadły (w sensie Minkowskiego) do wektora czteroprędkości. W naszym przypadku możemy po prostu sprawdzić, że tak jest w istocie wyliczając składowe wektora w i obliczając jego iloczyn skalarny (w sensie Minkowskiego) z u.

Ciąg dalszy nastąpi.







Komentarze
Pokaż komentarze (63)