Władysław Kosiniak-Kamysz na prezydenta kandydat w programie Kawa na Ławę zapytał retorycznie, czy jest sens, żeby schorowany 59latek nie mógł głosować korenspondencyjnie, a tryskający zdrowiem 60latek mógł.
Mój komentarz – Czy jest sens, żeby dobrze uczący się 17latek, olimpijczyk z matematyki lub historii (więc mający predyspozycje do logicznego myślenia, ew. znający historyczne związki przyczynowo-skutkowe), oglądający serwisy informacyjne i czytający gazety, więc świetnie zorientowany w aktualnej sytuacji politycznej – nie miał prawa brać udziału w wyborach, a 18latek, który ledwo na miernych skończył podstawówkę, 2 razy nie zdał z klasy do klasy, niczym się nie interesuje poza piciem piwa – takie prawo miał?
Potem w programie poseł Horała tłumaczył red. Olejnik czym są procenty. Red. Olejnik była zaniepokojona lawinowym wzrostem zachorowań na koronawirusa, poseł Horała trwał na stanowisku, że procentowo spada, a to się liczy. Jeśli poseł Horała miał na myśli tylko dzisiejszy wzrost to nie miał do końca racji, gdyż badane dane są często zaszumione i takie jednostkowe odchylenia są traktowane jako szum pomiarowy. Musimy poczekać jeszcze parę dni, żeby zobaczyć czy zmiana jest trwałą.
Ale proszę Państwa, mamy komputer i możemy się pokusić o bardziej skomplikowane obliczenia niż procenty. I każdy może z Państwa może zrobić sam te obliczenia – zaraz pokaże jak.
Najpierw trochę intuicji. Jeśli mamy zarażonego jednego pacjenta zero w dniu zero i zakładamy, że jedna osoba zarazi kolejną w kolejnym dniu liczba zarażonych będzie wynosiła w kolejnych dniach – 1, 2, 4, 8, 16, 32, 64. 128... gdyż każda zarażona osoba będzie zarażała kolejne. Różnica między ilością zarażonych w danym dniu i poprzednim jest dokładnie taka jak ilość zarażonych w dniu poprzednim, bo każdy kogoś zaraził (zgodnie z założeniem). Przy takim założeniu rozprzestrzeniania się wirusa 30mln dorosłych obywateli może się zarazić w 25 dni.
Oczywiście wirus nie rozprzestrzenia się tak szybko, ale model jest podobny. Model nie jest w 100% dokładny, bo nie uwzględnia dopływu zarażonych z zewnątrz, ale zawsze jakieś to przybliżenie. Możemy policzyć też szybkość rozprzestrzenia się wirusa.
Zaczynamy od zebrania danych. Pod tym adresem można sobie zobaczyć.
https://www.arcgis.com/apps/opsdashboard/index.html#/deaceebc69a3412c8b7699e3e025e213
Jak widać jest to wzrost wykładniczy (zgodnie z naszym modelem). Dziś (29.03) jednak widać pewien dziubek, jak napisałem wyżej może to być szum pomiarowy. Same dane nie wyglądają na bardzo zaszumione, ale może to być mylące.
Można też kliknąć na zakładkę "Przyrost dzienny", ale nas będzie bardziej interesowała zakładka ze skalą logarytmiczną. A to dlatego, że logarytm jest jedną z funkcji odwrotnych do potęgowania, a i logarytmując funkcję wykładniczą możemy uzyskać linię prostą, którą zresztą widać, choć wygiętą w delikatny łuk.
Na stronie https://octave-online.net (bez logowania!) mogą Państwo przeprowadzić teraz stosowne obliczenia. Na samym dole jest linia poleceń, które należy kopiować z mojego bloga. Polecenie wykonane jest po naciśnięciu "enter".
Zaczynamy od wprowadzenia danych (tych ze strony):
z=[5 6 11 17 22 31 51 68 104 125 177 238 287 355 425 536 634 749 901 1051 1221 1389 1638 1717]
musimy wygenerować jeszcze czas:
x=[1:size(z)(2)]
jak widać wygenerowany jest wektor 1 – 24, bo mamy próbki z 24 dni (wyrzuciłem kilka niereprezentacyjnych próbek z początku wykresu, kiedy był tylko 1 pacjent).
Możemy narysować sobie wykres (taki sam jak na stonie):
plot(x,z)
Logarytmujemy:
y=log(z)
I w skali logarytmicznej też możemy sobie zrobić wykres (hold off narysuje wykres na nowym rysunku):
hold off
plot(x,y)
Chcemy aproksymować linią prostą ten wykres. Żeby to osiągnąć zrobimy pewien algotymiczny myk:
X=[x' ones(1,size(x)(2))']
Stworzyliśmy macierz, gdzie 1szy rząd to wektor ze logaryrmowaną ilością zachorowań a drugi to jedynka.
[5 1
6 1
11 1
...
1717 1]
Aproksymacja prostą polega na ustaleniu parametów a i b w równianiu prostej y=ax+b znanym ze szkoły podstawowej.
W zapisie macierzowym – a tu już mamy poziom akademicki studiów nauk ścisłych i podobnych, więc proszę się skupić (poniżej to nie komenda, a tylko równanie).
Y=AX
Macierz A będzie zawierać współczynniki a i b. Dlatego macierz X uzupełnilismy jedynkami, bo
y=ax+b*1 (nasza nowa macierz A za jednym zamachem pomnoży x przez a i 1 przez b i wynik zsumuje)
Y to zlogarytmowana liczba chorych przedstawiona jako wektor kolumnowy – komenda:
Y=y'
apostrof robi transpozycję, czyli w wypadku wketora zamieni wierszowy na kolumnowy i vice-versa.
Teraz możemy aproksymować funkcję. (co robi "pinv" – dla zainteresowanych poniżej)
A=pinv(X)*Y
i voila! mamy parametry prostej... a jej równanie jest y=0.25566x+1.94276
Najbardziej intreresujący jest paramentr nachylenia prostej ~0,25, bo on tak na prawdę świadczy o postępie zachorowań.
Możemy narysować sobie wykres
hold on
plot(x,A(1)*x+A(2))
to 2 komendy: "hold on" sprawi, że kolejny wykres pojawi się na poprzednim, a nie jako nowy. "Plot" narysuje funkcje jak poprzednio.
Podsumujmy te kilka komend (jedna linia – jedna komenda):
z=[5 6 11 17 22 31 51 68 104 125 177 238 287 355 425 536 634 749 901 1051 1221 1389 1638 1717]
x=[1:size(z)(2)]
plot(x,z)
y=log(z)
hold off
plot(x,y)
X=[x' ones(1,size(x)(2))']
Y=y'
A=pinv(X)*Y
hold on
plot(x,A(1)*x+A(2))
11 linijek to chyba nie dużo jak na walę z wirusem. Ale widać, że nasza prosta bardziej przypomina cięciwę łuku i też jakoś w środku zawiązaną i nie wygląda na dobre przybliżenie.
Spróbujmy więc wykres przybliżyć 2ma prostymi. Widzimy lekkie załanie łuku około połowy wykresu. Wykonajmy 2 komendy:
y1=y(1:12)
x1=x(1:12)
A potem:
X1=[x1' ones(1,size(x1)(2))']
Y1=y1'
I...:
A1=pinv(X1)*Y1
hold on
plot(x1,A1(1)*x1+A1(2))
widzimy linię prawie dokładnie dopasowaną do pierwszych 12 dni
Dla drugiej prostej (każda linia poniżej to jedna komenda i trzeba je wklejać i naciskać enter jedna po drugiej):
y2=y(13:size(y)(2))
x2=x(13:size(x)(2))
X2=[x2' ones(1,size(x2)(2))']
Y2=y2'
A2=pinv(X2)*Y2
hold on
plot(x2,A2(1)*x2+A2(2))
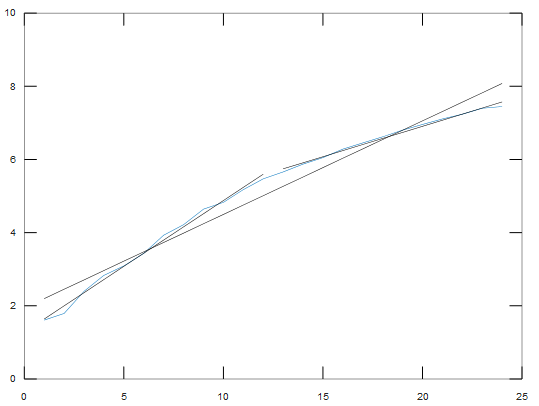
Czyli jak widzimy od 12 dni trend zachorowań jna koronawirusa jest mniejszy niż na początku. Nasza linia się teraz łamie z przerwą (dla drugiej proste dane wzięte od 13.03, a nie 12.03) i lepiej dopasowuje się do krzywej zachorowań.
Co się tało takiego 12 dni temu, poza tym, że było św. Patryka? 15.03 rząd zamknął granicę- jest to poza naszym modelem, gdyż on zakłada zarażanie się od osób zarażonych w Polsce a nie tych przybyłych ostatnio (zarażonych za granicą), ale ci zarażeni i tak wpływają na model. Więc zamknięcie granic na pewno sie dobrze przyczyniło. Ale wydaje mi się, że to ogół działań rządu, jak i rozsądek rodaków, którzy ograniczyli wychodzenie z domu. Zaraz po pojawieniu się wirusa większość z nas jednak więcej wychodziła z domu. Otwarte też były szkoły i inne miejsca publicznych spotkań. Te dwie proste też przybliżenie, a wskaźnik może stale maleć. No ale mają Państwo narzędzie do dalszych eksperymentów wystarczy zmienną "z" uzupełniać przez nowe dane.
Ważne tylko by nie wyciągać błędnego wniosku w nie w tą stronę, co potrzeba. Mniejszy wskaźnik rozprzstrzeniania się wirusa nie oznacza, że można obniżyć rygor. To zachowanie rygoru, jak unikanie wychodzenia z domu przyczynia się do spadku rozprzestrzenia się wirusa. Należy więc ten rygor zachować.
