UWAGA, UWAGA, oto Eureka wiedźmy Margo.
U Arkadiusza Jadczyka odbyła się rozmowa na temat krzywych i linii.
http://arkadiusz.jadczyk.salon24.pl/393897.html
Margo:
"A ja zapytam, co to są za linie?"
ARK:
Użyłem skrótu. Winno być "dwie linie proste, równoległe."
Na skrótach się zyskuje, ale za skróty się czasem płaci.
M.M.B.:
Ale ja miałam na myśli to, co napisał Tichy.
Tichy:
linie: linie proste
Z "krzywymi" jest w ogóle zamęt. Definicje, które pierwotnie nawet wydają się intuicyjne i "porządne", często zawarte w sobie mają paradoksy, czy też patologie...
I O TO CHODZI!
A czy wiecie, że tu można zrobić porządek?
Pozamiatać miotłą wiedźmy i zamęt zamieni się w porządek.
I to w bardzo prosty i elegancji sposób.
Nie wiem, jak Wy to zrobicie, ale sposób wiedźmy jest następujący:
Wszystkie linie i krzywe gładkie, i hiperbole, i parabole, a nawet elipsy i okręgi są JEDNYM I TYM SAMYM OKRĘGIEM znajdującym się w różnych stanach. Co powoduje te różne stany?
1.
To, co nazywam „wymiarem krzywizny” czyli mają one różne krzywizny.
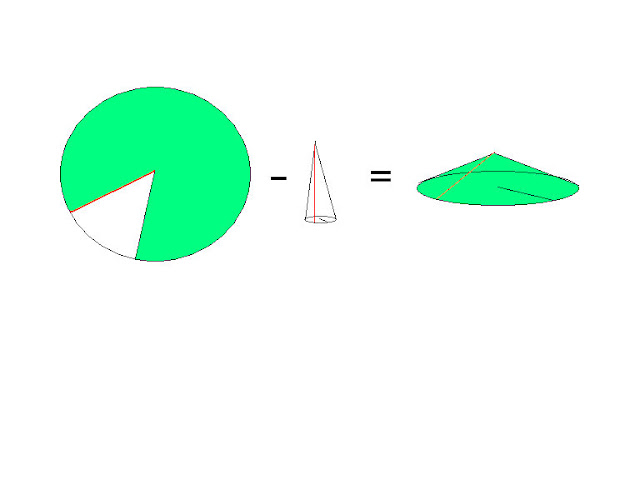
Teraz możecie dokładnie zrozumieć, co mam na myśli. Obwód koła (pole zielone plus białe) to okrąg po lewej stronie. Obwód ma przyrównany do jedności czyli równy 1, a obwód koła w innym stanie - zielony stożek po prawej stronie - jest pomniejszony o wycinek białego pola - biały stożek. Czyli nowe koło jest już zielonym stożkiem. Jego obwód - okrąg ma wartość ułamkową względem obwodu- okręgu z płaskiego koła.
Napisałam do Arka, ale do Was też przecież, bo możecie przeczytać, że kiedy:
a) parametr krzywizny k przyjmuje wartość ułamkową, wówczas każda krzywa gładka ma tę właściwość, że jej krzywizna jest ujemna.
b) parametr k przyjmuje wartości liczb naturalnych / całkowitych, wówczas każda krzywa gładka ma tę właściwość, że jej krzywizna jest dodatnia.
Oczywiście „lokalnie” czyli w każdym danym punkcie krzywizna jest zerowa, ale „ponadlokalnie”krzywizna jest dodatnia albo ujemna.
2.
Oczywiście okręgi mają różne promienie. Takie okręgi też są jednym i tym samym okręgiem znajdującym się w różnych stanach( o zróżnicowanej krzywiźnie). Ale tu każdy dowolny okrąg możemy „ubezwzlędnić” ( w jakiś sposób wyróżniamy jego indywidualny byt :-) To znaczy, że krzywizny innych okręgów można, a nawet należałoby „mierzyć” względem tego wyróżnionego.
To tyle na początek, żeby Was nie przemęczać. Zastanówcie się proszę nad tym. I jak ktoś dostrzeże w tym coś „niespójnego” to niechaj się ze mną podzieli swą uwagą lub myślami.
Pozdrawiam serdecznie
M.M.Boratyńska








Komentarze
Pokaż komentarze (2)