Jak już napisałem serię notek o liczbach (tu, tu, tu i tu), w której objawiłem (jak to napisał bloger Tichy) „obsesję rzekomego oderwania matematyki od rzeczywistości”, pora ma jej krytykę. Bo przecież wcale nie uważam, że matematyka jest „oderwana”, choć po przeczytaniu kilku owych notek tak mogłoby się wydawać. Wcześniejsze teksty poświęcone były liczbom, które pomimo „niedopasowania”, są wrośnięte w rzeczywistość, a przynajmniej w nasze jej rozumienie. Ale zgrzytów o podobnej naturze pomiędzy modelami matematycznymi a rzeczywistością, można znaleźć tyle, ile jest zastosowań matematyki. Jest tak dlatego, bo każde pojęcie matematyczne, nawet to najbardziej pasujące do fizycznego przypadku, ma cechy, których nie odnajdziemy w świecie materialnym.
Żeby się o tym przekonać zerknijmy na pierwsze poważne użycie matematyki w fizyce, czyli na opis oddziaływania Słońca i planet. W modelu sprowadza się on do potraktowania ciał niebieskich jako punktów materialnych, między którymi obowiązuje oddziaływanie grawitacyjne, czyli prawo odwrotnych kwadratów.

Punkt materialny to „zwykły” punkt o trzech współrzędnych z dołączoną masą. Od razu narzuca się pierwsza wątpliwość – planety mają niezerowe rozmiary! No i rzeczywiście – przyjęty model opisze ruch orbitalny, ale wirowego już nie.
W modelu wykorzystujemy pojęcie pochodnej. Żeby ją legalnie zdefiniować, musimy korzystać z tzw. przejścia granicznego – innymi słowy musimy policzyć granicę specjalnego ilorazu gdy mianownik i licznik dążą do zera. Na przykład przy liczeniu prędkości:
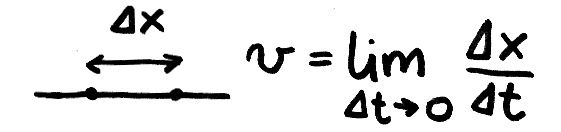
Owo przejście graniczne nie ma do końca odzwierciedlenia w fizyce, bo iloraz różnicowy nieodwołalnie traci sens gdy Δx jest rzędu odległości atomowych. Dla większości przypadków staje się tak znaczenie „wcześniej”. Przykładowo dla modelowania ruchu planet, może się wydawać, że wyrażenie różnicowe przestaje mieć przełożenie na rzeczywistość, gdy Δx jest rozmiaru planety. Aż tak źle na pewno nie jest, bo w modelu analizujemy ruch tzw. środków masy. Mimo to nie określimy ich tak dokładnie, jak wymagałyby tego współrzędne punktów, które są liczbami rzeczywistymi z „nieskończoną” dokładnością. I to nie tylko z powodów czysto pomiarowych. Nawet demon Laplace'a miałby kłopoty, bo nie wiedziałby które ciała (samoloty, rakiety satelity itp.) wliczać do planety Ziemi, a które nie.
Współrzędne sił, w modelu spuer-gładkie, bo ~1/r2, są pewnym uśrednieniem oddziaływań kwantowych, przy czym nie do końca wiemy jakich, bo grawitacji nie pokwantowano, ale raczej nie spodziewamy się, żeby było inaczej niż dla elektryczności. W końcu pytanie „z jaką siłą jądro atomowe przyciąga elektron?” nie ma sensu.
Jak widać model zgrzyta w wielu miejscach, ale mimo to większość fizyków uznaje, że zastosowane w nim pojęcia matematyczne są wrodzone dla ruchu planet. Zacznijmy od drugiej zasady dynamiki Newtona, która wprowadza nietrywialny związek między siłami a położeniem, właśnie poprzez drugą pochodną. Za pomocą rachunku różniczkowego zamiast trzech współrzędnych siły, możemy wprowadzić jedną funkcję energii potencjalnej. I nie jest to tylko matematyczna sztuczka, bo w mikroświecie ta ostatnia ma większy sens od sił. A wracając do planet i pochodnych: wisienką na torcie jest połączenie elips i hiperbol z siłami odwrotnie proporcjonalnymi do kwadratu odległości. Podsumowując: według fizyka, matematyka na pewno nie jest „oderwana”.
W tej sytuacji typowe flejmotwórcze pytanie „Dlaczego matematyka pasuje do rzeczywistości?” można z czystym sumieniem przeformułować na: „Dlaczego matematyka tak dobrze pasuje do rzeczywistości, skoro do niej nie pasuje?”.
Przypadków w których fizycy (moim zdaniem słusznie) „wierzą” w matematyczność przyrody jest więcej. W XIX i XX wieku równania różniczkowe z pochodnymi cząstkowymi stały się powszechnym językiem opisującym szerokie spektrum zjawisk fizycznych: Elektrony w atomach i ciałach stałych koniecznie chcą się słuchać równania Schrödingera. Przejawy oddziaływania elektrycznego podpadają pod równania Maxwella. Zaś geometria różniczkowa gra pierwsze skrzypce w grawitacji.
W ostatnim akapicie zrobiło się jakoś zbyt poważnie, więc koniecznie trzeba zmienić nastrój. Pogadajmy znów o liczbach. Może nie wszyscy wiedzą, ale liczby rzeczywiste mają nieoczywistą cechę: Można przedstawić jakąś liczbę jako sumę nieskończenie wielu składników, pozamieniać ich kolejność, zesumować od nowa i… uzyskać zupełnie inną liczbę. Nawet był taki żart jednego z polskich matematyków (zdaje się autorstwa Sierpińskiego albo Steinhausa), zachęcający do wpłaty na konto złotówki, podzielenia jej i zesumowania do miliona. „Wypłaćmy więc ten milion!” brzmiała puenta. Tak się nie da, bo akurat w działaniu na pieniądzach nie stosuje się liczb rzeczywistych, a twory nieco podobne w charakterze do liczb całkowitych z osobno określonymi działaniami, różnymi w zależności od zastosowań, nieco podobnymi do tych znanych z matematyki, ale nie do końca. Z pewnego punktu widzenia mają też trochę wspólnego z „liczbami Zenona”, które użyte w stosunku do Achillesa nie pozwoliły mu dogonić żółwia. Ale żeby nie było: do jednoznacznego sformułowania działań na pieniądzach – a chodzi głównie o zaokrąglenia – używa się właśnie liczb rzeczywistych! No bo jak inaczej?
* * *
To prawda, że nie da się podzielić danego przedmiotu dokładnie na pół. Nie oznacza to jednak, że nie powinniśmy używać ułamków do opisywania dzielenia tortu czy odsypywania pół kilograma mąki do upieczenia ciasta. Używajmy, tym bardziej, jeśli chcemy przeliczyć ilość składników, zwiększając je półtora raza w stosunku do początkowego przepisu.







Komentarze
Pokaż komentarze (39)