Sądząc po, jeszcze nieujawnionych, wynikach powyższy kalkulator jest jedynym dopuszczonym do stosowania w Podkomisji. Można dodawać, mnożyć itp. A w wyniku zawsze wychodzi jedyny, pożądany zamach.
Są dostępne jednak i inne kalkulatory. Np. kalkulator wybuchów np. Kalkulator parametrów wybuchu Kingery-Bulmash przetestowany dla różnych materiałów wybuchowych od poniżej kilograma do 400 ton. Ten zakres chyba jest wystarczający by wyliczyć to, co mogłoby się stać w Smoleńsku, gdyby tam był faktycznie tak pożądany wybuch. Każdy może go otworzyć i sprawdzić osobiście wymysły „ekspertów”.
https://unsaferguard.org/un-saferguard/kingery-bulmash
https://iv.pl/images/33eca038261c6fb40553daea3a2c9b36.png
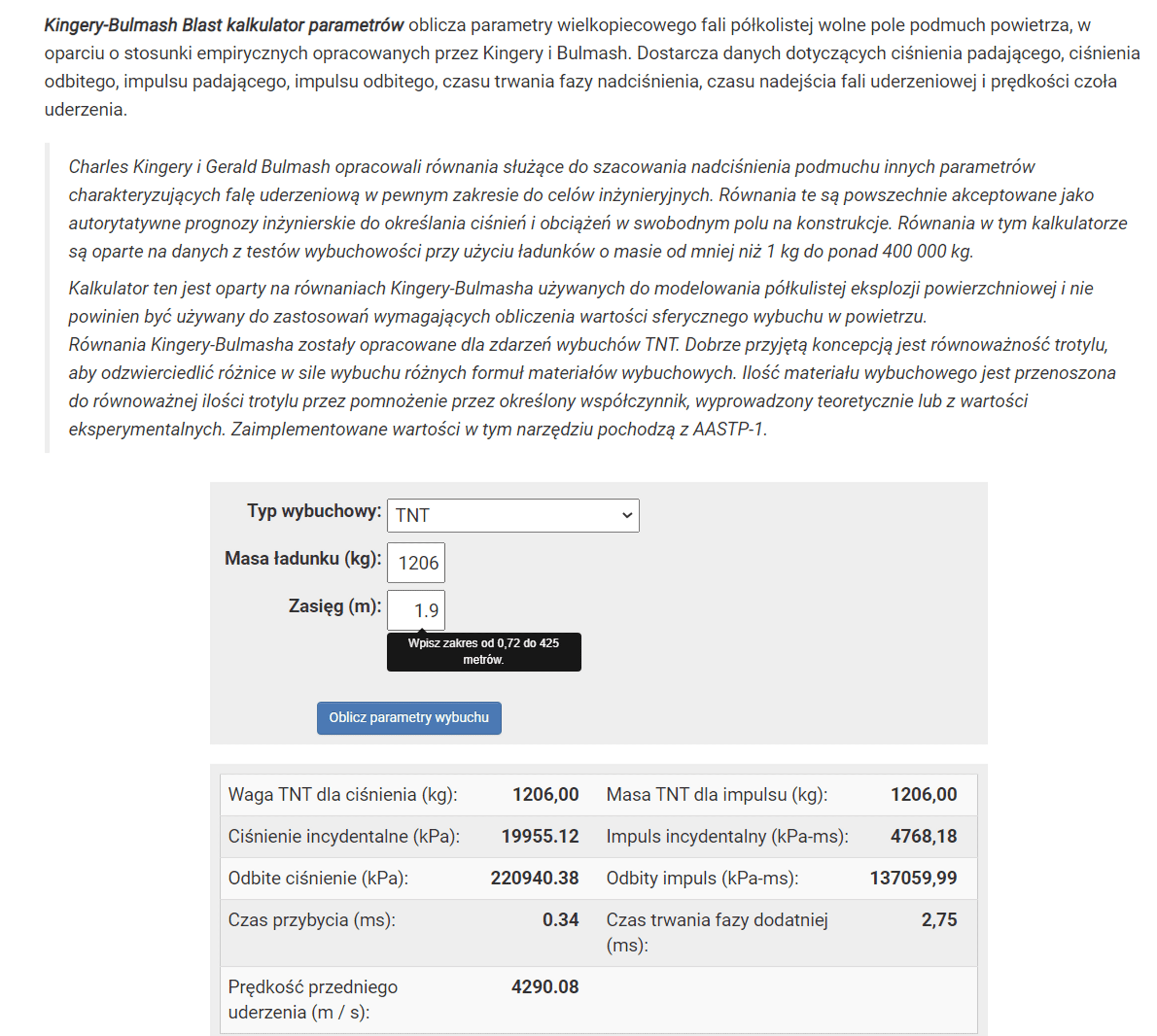
Każdy może go otworzyć i pokalkulować, choćby to o czym piszę. Tłumaczenie jest automatyczne a nie jakietakie.
Jest tu zastrzeżenie, że jest to wybuch w półsferę. Wybuch w całą sferę nie posiadałby parametrów związanych z odbiciem, co jest oczywiste ponieważ nie ma od czego się odbić. Gdyby ktoś liczył parametry wybuchu w wywierconym otworze np. górotworu to powinien użyć wyłącznie parametry wybuchu odbitego.
Na obrazku widać rachunki dla 1206 kg TNT w odległości 1,9 m. Skąd takie dane?
Przez drzwi samolotu można włożyć beczkę o rozmiarach: średnica 74 cm, wysokość 175 cm.
Jej objętość wynosi pi*(0,37 m)^2*1,75 m=0,752 m^3. Razy gęstość TNT 1600 kg/m^3 daje właśnie to 1206 kg.
Wyliczone parametry do dalszych obliczeń to Impuls incydentalny 4768,18 kPa*ms = 4768,18 Pa*s.
Ciśnienie incydentalne (maksymalne) ok. 200 atm.
Rozpocznijmy od ciśnienia. Maksymalna siła działająca na drzwi to
F = 200 atm * 0,8 m * 1,8 m = 288*atm*m^2; 1 atm to 10,3 Ton/m^2 ostatecznie
F=3000 Ton.
Tak wielka siła, by nie rozedrzeć drzwi musiałaby uderzyć jednocześnie na całą powierzchnię (efekty termiczne pomijam choć są one ogromne). To może zapewnić jedynie ładunek o kształcie walca z osią zgodną z osią samolotu (czyli ta beczka musiałaby leżeć na podeście o wysokości ok. 23 cm).
Do jakiej prędkości może rozpędzić takie drzwi wybuch 1,2 t TNT?
M * V = Impuls incydentalny. M drzwi = 78 kg, Impuls incydentalny 4768,18 Pa*s
V = 4768,18 Pa*s/78 kg = 4768,18/78 (kg*m/s^2) *s /kg = 61 m/s.
Czyli tak potwornie wielki ładunek daje tylko połowę tego co potrzebują podkomisjanci.
Był prezentowany przez podkomisję wybuch modelu. Użyto ok. 3 kg materiału wybuchowego i rozniósł on model w strzępy.
Natomiast na filmie z prof. Biniendą
https://www.youtube.com/watch?v=2X36o1uGZq8
widać, że wybuch nie rozerwał samolotu, czyli materiałów wybuchowych powinno być mniej. A ile.
Z danych Tu-154 wynika, że w kabinie pasażerskiej nie powinno być więcej niż 0,7 atm. Pomnożone przez współczynnik bezpieczeństwa 2 daje to 1,4 atm czyli 140 kPa. Z kalkulatora Kingery-Bulmash możemy wyznaczyć ilość MW dla takiego ciśnienia, wynosi ona 0,333 kg dla ładunku ułożonego w osi samolotu 1,9 m od poszycia. Impuls incydentalny 69,65 Pa*s, Wyliczona prędkość to 69,65/78 m/s = 0,89 m/s. To jest rząd wielkości wyliczony naprędce przez You-Know-Who.
W Internecie można znaleźć test wybuchu 1/3 kg MW. Jest to test z Lockheed Tristar.
https://www.youtube.com/watch?v=HHP1JeyiKZw
Najlepiej to widać od 1 min 25 s po spowolnieniu do 0,25 prędkości. Ładunek nie był w osi dlatego wyrwał rozdrobniony kawał poszycia. Po kilku sekundach filmu eksplozja gaśnie a rozpoczyna się gwałtowny wypływ ok 1 tony (czyli masa 3000 razy więsza niż ładunek MW) nadmiarowego powietrza symulującego nadciśnienie statyczne przy locie na wysokości przelotowej. Jest to różnica między ciśnieniem w kabinie, standardowo odpowiadająca wysokości 2400 m, czyli 75 kPa a wysokością 11000 m czyli 22,6 kPa. Różnica wynosi 52,4 kPa. Porównany to z ciśnieniem w dyszy silnika Tu-154M.
Siła ciągu 105 kPa, średnica dyszy 1,2 m.
Ciśnienie wynosi
p=F/S=105 kN/(pi*0,6^2 m^2) = 93 kPa. Ciśnienie testowe w Tristar to 56% maksymalnego ciągu (70% maksymalnych obrotów).
To właśnie wypływ powietrza dokonuje takich spustoszeń. W tupolewie nadciśnienia statycznego nie było.
Wystrzelenie drzwi to obrzydliwa bajka serwowana Polakom. Drzwi nie mogą osiągnąć w opisywanej sytuacji aż 125 m/s, również dlatego, że przy tej prędkości należałoby użyć ponad 2500 kg TNT. Drzwi spłonęłyby w kuli ognia. Ludzie wyparowali.
Drugą częścią filmu jest dolot drzwi z wysokości 9 m.
Przy prędkości pionowej 125 m trwałoby to 0,072 s. Drzwi musiałyby odpowiednio pionowo ustawić, a aerodynamika ustawia tak by był najmniejszy opór. Tak jak na rysunku, w kierunku V_II
https://iv.pl/images/8d8b8684328a8f63e81330fd708dd235.png
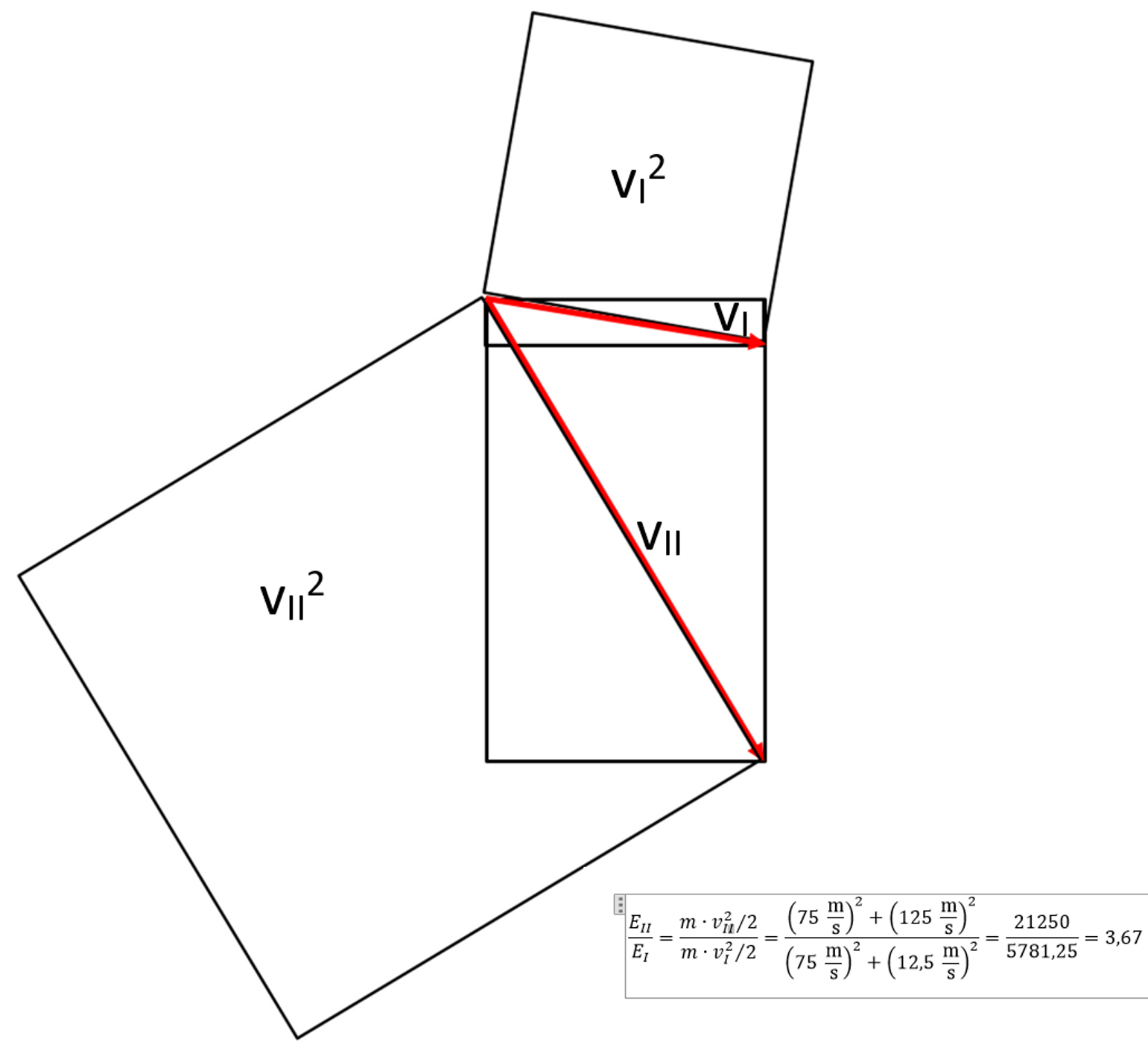
Przy okazji wyjaśniam absurd, tak często powtarzany przez podkomisjantów, o 100 razy większej energii przy zmianie prędkości spadania z 12,5 m/s do 125 m/s (przy prędkości poziomej 75 m/s). Są wyrysowane prędkości, ich kwadraty i wyliczona proporcja energii. Wynosi ona tylko 3,67 razy. Kto mówi, że to 100 razy bezczelnie oszukuje, zwłaszcza wtedy gdy twierdzi, że jest fizykiem.
Zakładając, że w czasie 0,072 s drzwi wyhamują z 72 m/s do 30 m/s, należałoby przyjąć współczynnik oporu Cx=23, podczas gdy maksymalny dla wklęsłej czaszy wynosi 1,42 a do tego, że drzwi nie hamują ruchu w pionie a tylko w poziomie, co jest oczywistym absurdem. Bo w praktyce hamuje jedno i drugie, ale zdecydowanie słabiej. I o tym już była mowa w notkach u innych.
Wykres wyliczony na podstawie znanych wzorów przedstawia w zależności od czasu: linia zielona – droga przebyta przez drzwi poziomo (3,3 m); linia niebieska prędkość w m/s; linia czerwona opóźnienie w jednostkach g (od 140 g do 24,5 g).
https://iv.pl/images/94ae4f6deecedba918671e4edc69e5a3.png










Komentarze
Pokaż komentarze (74)