Smoleńsk wraca, po dłuższym czasie postanowiłem więc napisać coś o podstawach modelowania komputerowego. Moim celem nie jest chęć udowodnienia że jakaś hipoteza katastrofy jest prawdziwa lub nie. Raczej chce wykazać podstawowe błędy warsztatowe ludzi Macierewicza.
Podwładni Macierewicza z zapałem zgniatają puszki, śledzą propagacje rysy w membranie parówki a nawet używając "najszybszych" komputerów w Ohajo liczą metalowe powłoki skrzydła. Robią to bez głębszego zrozumienia problemu, teorii i jej podstaw. Nie ma w tym nic złego, gdyby nie to, że na podstawie swych rzeczywistych, umysłowych lub numerycznych eksperymentów wysuwają wnioski, do których nie ma podstaw, jak pokaże poniżej. W konsekwencji te błędne wnioski będą prowadzić do błędnych decyzji, niesłusznych oskarżeń i wypaczeń rzeczywistości. Dziś, z trudnych do zrozumienia dla mnie przyczyn, ludzie zespołu Macierewicza (może z powinno być z zespołem Macierewicza) mają moc sprawczą, są członkami rządowej komisji.

Tym motywowany, z syzyfowym zapałem zademonstruje na już kultowym przykładzie zgniatanej puszki (zob. rys 1) jak błędne mogą być obiczenia numeryczne gdy są wykone bez odpowiedniej staranności i wiedzy. Z masy różnych błędów, dla klarowności, wybieram ten podstawowy który jest wymieniany przez wielu wcześniej, tzn. pokaże że obliczenia z zbyt rzadką siatką prowadzą do ogromnych błędów.
Wymiary i obciążenia cylindra (puszki) przyjęte są za [1] oraz [2,3,4,5]. Do wstępnych obliczeń użyta została siatka o bardzo małej rozdzielczości. Następnie siatka została zagęszczana aż wyniki uległy stabilizacji, to znaczy zaczęły być zbieżne do dokładnego wyniku. W tej procedurze nie ma nic szczególnego, tak powinno postępować się zawsze, to jest warsztat.
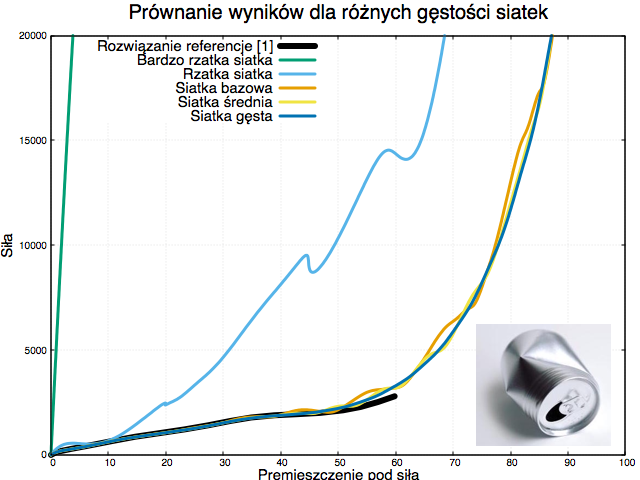
Za każdym razem gdy zagęszczana jest siatka, obliczone siły maleją a przemieszczenia rosną, tzn. odpowiedź powłoki jest mniej sztywna. Takie zachowanie jest oczekiwane i zgodne z teorią, wynikają one z twierdzenia 1.2 w [6]. Zatem w przypadku rzadkiej siatki rozwiązanie przeszacowuje sztywność struktury i niedoszacowuje odkształcenia.
Zbyt rzadka siatka prowadzi do wyników nierzeczywistych. Zatem sztuczne zwiększanie jakikolwiek innych parametrów traci cel, gdy sama rozwiązania jest błędne, bez znaczenia jakie parametry zostały wprowadzone. Dodatkowo jeżeli kryterium zniszczenia jest odkształceniowe (jak u Biniendy), materiał wydaje się super wytrzymały, gdzie naprawdę odkształcenia są niedoszacowane, zob rys 2. Pierwszy i drugi wykres dla rzadkich siatek, niedoszacowuje znacznie przemieszczenia. W przypadku najrzadszej siatki błąd jest ponad 1000%.
Nie wiem jak wielkie błędy numeryczne są w symulacji Biniendy, sądząc po rozdzielczości siatki skrzydła i modelu drzewa mogą być bardzo duże, rzędu tych w załączonym tu przykładzie. Członek rządowej komisji Macierewicza nie przeprowadza analizy zbieżności tym bardziej poddając pod wątpliwość swoje wyniki.
Wyniki otrzymane przy małej rozdzielczości siatki są niemiarodajne a wysuwanie na ich podstawie wniosków nieuprawnione. Nawet gdyby dokonano obliczeń przy zachowaniu pełnej staranności, obliczenia komputerowe nie mogą być punktem wyjścia do stawiania hipotezy o przyczynach katastrofy, co najwyżej w szczególnych przypadkach mogą tą hipotezę wzmacniać. Budowanie wniosków na podstawie samej symulacji i osobistych przekonań nie popartych twardymi dowodami jest dużym nadużyciem. Sprawia to wrażenie celowej manipulacji opinią publiczną (zobacz wywiad https://youtu.be/RmDzBc_XrC0?t=3m26s), przedstawiając obliczenia wykonane za pomocą zaawansowanych narzędzi, gdy w rzeczywistości same obliczania są mało warte.
Trudno mi uwierzyć że błędy warsztatowe popełniane przez prof. Biniende są nieświadome. Jest profesorem niezłego ( przeciętnego ) amerykańskiego uniwersytetu. Wytłumaczeniem może być to, że w pełni świadomie manipuluje, a za tą niechlubną pracę na rzecz Macierewicza i partii został nagrodzony, prestiżową funkcją i niezłą pensją.
[1] Hosseini, Saman, et al. "An isogeometric solid‐like shell element for nonlinear analysis." International Journal for Numerical Methods in Engineering 95.3 (2013): 238-256.
[2] Lindberg GM, Olson MD, Cowper GR. New development in the finite element analysis of shells. Quarterly Bulletin of the Division of Mechanical Engineering 1969; 4:1–38.
[4] Bucalem ML, Bathe KJ. Higher-order MITC general shell elements. International Journal for Numerical Methods in Engineering 1993; 36:3729–3754.
[5] Saleeb AF, Chang TY, Graf W, Yingyeunyong S. A hybrid/mixed model for non-linear shell analysis and itsapplication to large rotation problems. International Journal for Numerical Methods in Engineering; 29:407–446.
[6] Demkowicz, Leszek. Computing with hp-ADAPTIVE FINITE ELEMENTS: Volume 1 One and Two Dimensional Elliptic and Maxwell problems. CRC Press, 2006.










Komentarze
Pokaż komentarze (66)