Serię notek o podzbiorach Rn, kończę tekstem wychodzącym poza główny temat, choć nawiązuje on do poprzedniego o twierdzeniu Emmy Noether. Trochę więcej w nim fizyki niż matematyki. Mam nadzieję, że fizyki ciekawej…
W poprzednim odcinku zgrubnie poznaliśmy jak twierdzenie Noether łączy symetrie z prawami zachowania. Istnieją jednak przekształcenia, które bez wątpienia są symetriami, a nie mają wiele wspólnego z tym twierdzeniem. A są nimi najbardziej podstawowe symetrie mechaniki klasycznej.
Transformacje Galileusza
Wiemy, że transformacje Galileusza opisują zmianę jednego układu inercjalnego w inny. Można również się dowiedzieć, że równania Newtona są niezmiennicze względem tych przekształceń. Oznacza to, że rozwiązując równania w każdym takim układzie odniesienia, dostaniemy równoważne wyniki. W tym sensie są to symetrie równań. W odróżnieniu od symetrii stosowanych w twierdzeniu Noether, nie są to przekształcenia przestrzeni na której określono równania Newtona, ale zmiany układu współrzędnych.
Wypiszę postać transformacji dla przypadku, gdy jeden układ porusza się względem drugiego wzdłuż osi X z prędkością u:
x' = x - ut
y' = y
z' = z
Kiedy zróżniczkujemy powyższe wzory po czasie, dowiemy się, jak będą transformować się prędkości:
v'x = vx - u
v'y = vy
v'z = vz
Niezmienniczość równań Newtona względem tych transformacji zapewniona jest przez to, że występuje w nich druga pochodna położenia czyli przyspieszenie. Kiedy zróżniczkujemy powyższy wzór jeszcze raz, dostaniemy a'x=ax. Czyli przyspieszenie we wzorze ma=F nie zależy od u.[1]
Gdyby jednak kogoś korciło potraktować u jako parametr grupy przekształceń twierdzenia Noether, to od razu go uspokajam. Energia kinetyczna nie jest niezmiennicza według tych przekształceń. Co oznacza, że żaden rozsądny lagranżian nie będzie ich niezmiennikiem, więc założenie twierdzenia nie będzie spełnione.
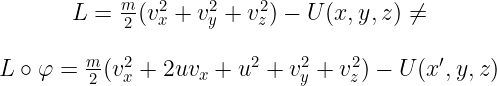
Spotkałem się z próbami „poprawiania” lagranżianu, żeby jednak przekształcenie Galileusza było symetrią w sensie twierdzenia Noether. Ale były to próby albo wybitnie żałośliwe, albo wymagające użycia dość mocnej transformacji czasu, będącej czymś w rodzaju pozostałości po transformacjach Lorentza.
Odwrócenie czasu…
…czyli transformacja t → -t.
Zanim zaczniemy roztrząsać tę symetrię, zauważmy, że odwrócenie czasu zmienia zwrot prędkości. W wyrażeniu różnicowym (Δq/Δt) musimy zamienić miejscami położenie początkowe i końcowe, co spowoduje zmianę znaku. Jest to zgodne z intuicją „cofania w czasie” poprzez odwrócenie klatek w filmie. Jeśli samochód jechał od lewej krawędzi kadru do prawej, to po odwróceniu kolejności wyświetlania, będzie poruszał się w przeciwną stronę.
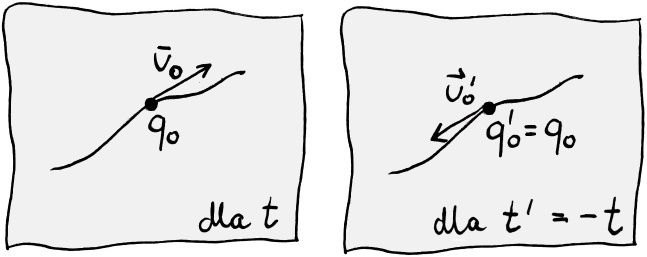
Ma to swoje konsekwencje w przyjęciu warunków początkowych: Stan początkowy (q0, v0), po zamianie czasu przetransformuje się do (q0, -v0). Będzie się to też tyczyć prędkości w reszcie stanów.
Za to dla przyspieszenia zmiany zwrotu nie będzie: w wyrażeniu (Δv/Δt) zamiana kolejności prędkości zniweluje ich przeciwny zwrot i a → a'=a.
Wróćmy do symetrii. Jeśli ograniczymy badane siły do takich, co nie zależą od czasu i prędkości, dostaniemy symetrię w sensie formalnym. Bo w równaniach Newtona:
F = ma
nie wystąpią wielkości, które mogłyby się zmienić przy tym przekształceniu – we wzorze na siłę nie wystąpią zmienione v i t. Można uczciwie powiedzieć, że takie przekształcenie zachowuje postać równania Newtona. Jak jednak zobaczymy poniżej „zachowanie postaci równań” nie jest wcale warunkiem koniecznym zadziałania symetrii.
Powyższe ograniczenie jest dość mocne i nie obejmuje wielu istniejących w przyrodzie sił. A przecież w wielu miejscach można usłyszeć, że równania Newtona są odwracalne w czasie bez dodatkowych warunków. Więc jak to jest? Trzeba przyjrzeć się trochę dokładniej z czym mamy do czynienia.
Jak działają siły na takie „odwrócone w biegu” ciało? Jeśli siła przyspieszyła ciało, to po odwróceniu czasu, taka sama siła będzie je zwalniać. I działa to identycznie dla sił zależnych od położenia (np. pole sił elektrycznych), jak również od czasu (np. włączanie i wyłączanie silników odrzutowych).

Podobnie wygląda zmiana kierunku pod wpływem siły, co przedstawia poniższy rysunek:
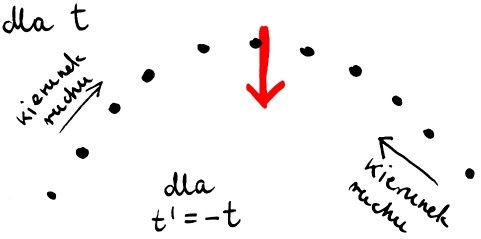
Podsumowując: Symetria zmiany kierunku czasu obowiązuje dla wszelkiego rodzaju sił. Nawet wtedy, gdy „postać równań” Newtona nie jest zachowana – to znaczy nie tylko dla sił zależnych od położenia. I tym optymistycznym akcentem można by zakończyć notkę, gdyby nie to, że czasami oglądamy filmy „odwrócone w czasie” i jednak potrafimy rozpoznać, że są cofnięte. Do wyjaśnienia tej niezgodności używa się argumentów natury statystycznej, bo na filmach oddziałujących ciał jest zwykle dużo. Mimo to da się odnaleźć rysy na odwracalności w czasie równań newtonowskich, nawet dla pojedynczej cząstki.
Przyjrzyjmy się mianowicie oddziaływaniom, które zależą od prędkości. Według mojej wiedzy w przyrodzie istnieją dwie możliwości wystąpienia takich sił:
- siła prostopadła do prędkości – tak jest dla siły Lorentza, gdy wpuszczamy naładowaną cząstkę do pola magnetycznego F = qv×B.
- siła równoległa do prędkości i przeciwnie zwrócona – wszelkiego rodzaju opory ruchu.
No i tu mamy pewne problemy.
W przypadku siły Lorentza problem jest pozorny, choć od razu tego nie widać. Na czym polega? Zauważmy, że cząstka z „odwróconą” prędkością, a co za tym idzie z przeciwną siłą, będzie zakreślać kółka „w drugą stronę”.
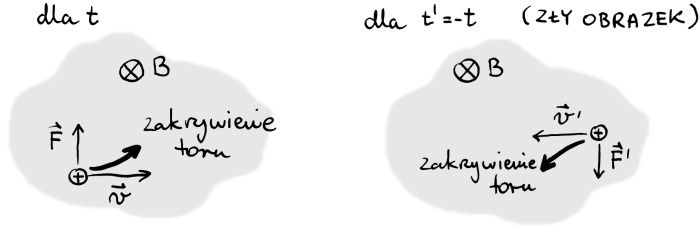
Żeby się uratować przed taką sytuacją, musimy założyć, że zwrot B też musi zostać zmieniony. Sam wzór na siłę Lorentza nie stanowi bynajmniej definicji siły, ale pola[2]. Tak więc nie będzie on wystarczającym kryterium, co do zachowania postaci F. Istnieją jednak argumenty natury elektrycznej, że przy transformacji powinniśmy przemnożyć wektor pola magnetycznego przez -1, no a wtedy siła się nie zmieni. Otóż pole B jest wynikiem istnienia prądu j i zależy od niego liniowo. Prąd jest zaś proporcjonalny do prędkości ładunków. Skoro po odbiciu czasu zmieniamy zwrot prędkości, zmienimy też kierunek prądu, a co za tym idzie zwrot pola.
Pozostają jeszcze siły równoległe do prędkości. Tu mamy poważniejszy kłopot, choć wydaje się, że obrazek z przyspieszaniem/zwalnianiem jaki narysowałem kawałek wyżej, obowiązuje. Na przykład hamująca siła tarcia przetransformuje się na przyspieszającą (β to iloczyn wartości siły nacisku i współczynnika tarcia):
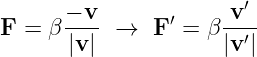
Czy aby na pewno teraz jest dobrze? Zauważmy, że w spisie sił zależnych od prędkości nie ująłem sił o kierunku zgodnym z prędkościami. Osobiście nie znam takich sił. Zresztą mam podejrzenia, że stanowiłyby coś w rodzaju perpetuum mobile. Bo odwrócenie czasu z sił tarcia robi „dopalacze” zwielokrotniające prędkość ciał. Tak więc symetria dla czasu załamuje się z powodów „praktycznych” – w przyrodzie nie ma sił, które byłby zależne od prędkości i jeszcze z nimi zgodne. Czyli jeśli mamy stół bilardowy z jedną bilą, której ruch został sfilmowany, to potrafimy ocenić, czy film jest odwrócony w czasie czy nie.
Tak jest w skali makro, bo w skali mikro – o ile można jeszcze mówić o prawach mechaniki klasycznej – nieodwracalność czasu jest tłumaczona argumentami statystycznymi. Odwracalne oddziaływania elektryczne w skali mikro, użyte do przeogromnych liczb cząstek, tworzących ciała w skali makro, „uśredniają się” do nieodwracalnych sił oporów ruchu.
[1] Powstaje pytanie czy zawsze działająca na ciało siła F nie będzie zależała od u? Rozsądek podpowiada, że cecha układu odniesienia (u) nie powinna mieć znaczenia dla rzeczywistości (F). Ale odpowiedź na to pytanie nie jest tak oczywista. Można zajrzeć do notki „Ładunek, prąd i STW”, żeby się okazało, że wcale tak nie jest, gdy włączymy pole magnetyczne. Wtedy zasada względności Galileusza się nie stosuje! Dziwne? Od kiedy wiadomo, że pole magnetyczne jest efektem relatywistycznym, nie jest to dziwne. Równania Newtona są przybliżeniem relatywistycznej dynamiki STW. Jeśli chcemy mieć prawidłowe równania obejmujące efekty relatywistyczne, musimy stosować STW, gdzie transformacje Lorentza są w pełni kompatybilne z wpływem pola e-m na badane ciało. Ale żeby nie było, że podręczniki kłamią w sprawie relacji Newton-Galileusz: Równania Newtona z włączonym polem magnetycznym nie są niezmiennicze względem przekształceń Galileusza, ponieważ samo pole magnetyczne jest „sprzeczne” z tymi przekształceniami.
[2] Nawiasem pisząc, wzór na siłę Lorentza wyznacza nam nie kierunek pola magnetycznego, ale płaszczyznę – wspólną dla siły i prędkości (o takim kierunku, że siła jest największa). Ponieważ jednak łatwiej nam operować jednowymiarowym wektorem B niż dwuwymiarowym „czymś” (to „coś” nazywa się biwektor), umawiamy się, że prostopadła do tej płaszczyzny ma stanowić kierunek wektora. A już zwrot dla tego kierunku, jest czysto umowną kwestią.







Komentarze
Pokaż komentarze (28)